1, Stack method area, method call, recursion, etc   

 

1. Object class stack method area

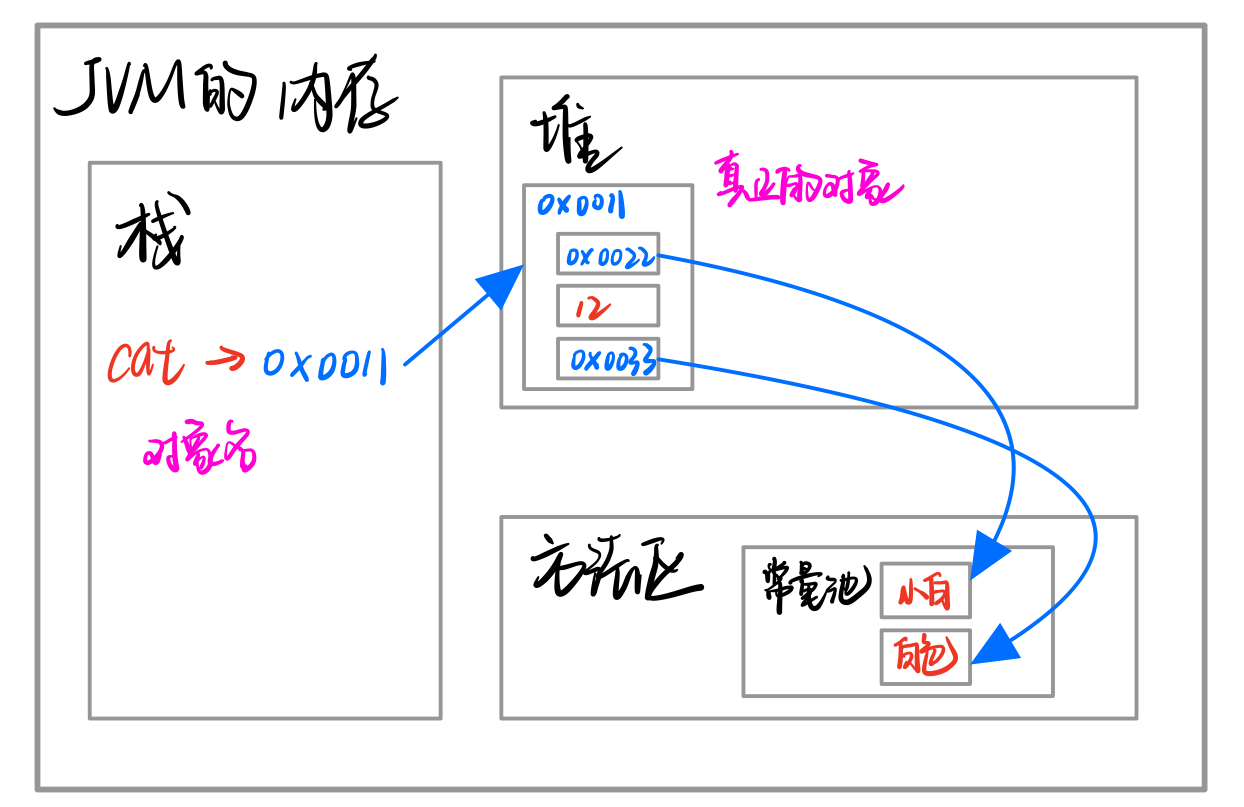
Cat cat = new Cat();
cat.name = "Xiaobai";
cat.age = 12;
cat.color = "white";

The string is a reference type and will be placed in the constant pool of the method area

  ① The syntax of attribute definition is the same as that of variable. Example: access modifier attribute type attribute name;

Access modifiers: public, proctected, default, private -- control the access range of attributes

② The definition type of property can be any type, including basic type and reference type

③ If the property is not assigned a value, it has a default value. The rule is the same as that of an array

Person p1 = new Person();
//Create a Person object, p1 is the object name, and the object space (data) created by new Person() is the real object
//The default value of the property of the object follows the array rules, int 0, short 0, float 0.0, char \u0000

How to create an object:

//Declare before create
Cat car; //Declared object Cat, declared in the stack, space is not allocated
cat = new Cat(); //Create, open up space in the heap, initialize by default, and then return the address value to the declaration in the stack

//Create directly
Cat cat = new Cat()
//First load Cat class information (attribute and method information, which will only be loaded once), and then allocate space in the heap,
//Default initialization: assign the address to cat, and cat will point to the object for specified initialization

Memory allocation mechanism of classes and objects:

① Stack: general storage of basic data types (local variables)

② Heap: store objects (cat, cat, array, etc.)

③ Method area: constant pool (constant, string), class loading information

Example:

Person a = new Person();
a.age = 12;
a.name = "Xiao Ming";
Person b;
b = a;
System.out.println(b.name);
b.age = 200;
b = null; //Leave the address blank
System.out.println(a.age);
System.out.println(b.age);

Output:
Xiao Ming
200
b.age An exception will occur (because the address is set to null and the null pointer is abnormal)

2. A method can have at most one return value. If multiple results are returned, an array is returned

Classes include methods and attributes. There can be multiple classes in a piece of code, but there is only one main class

Methods cannot be nested

Methods in the same class can be called directly

Cross class call: if method a in class a wants to call method B in class B, it needs to create class B object m in method a, and then call method B (m.b)

3. Method call summary:

① When the program executes the method, it will open up an independent space (stack space)

② When the method is completed or executed to the return statement, it will return

③ Return to the place where the method was called

④ After returning, continue to execute the code after the method

⑤ When the main method (stack) is executed, the whole program exits

Note: each time a method is called, an independent stack space is opened in the stack

4. Basic data type. The value (copy) is passed. Any change of formal parameter cannot affect the actual parameter

The reference type passes the address. The change of formal parameter will affect the actual parameter

5. Recursive call of method

Recursion returns from the top stack

  Recursion of factorials

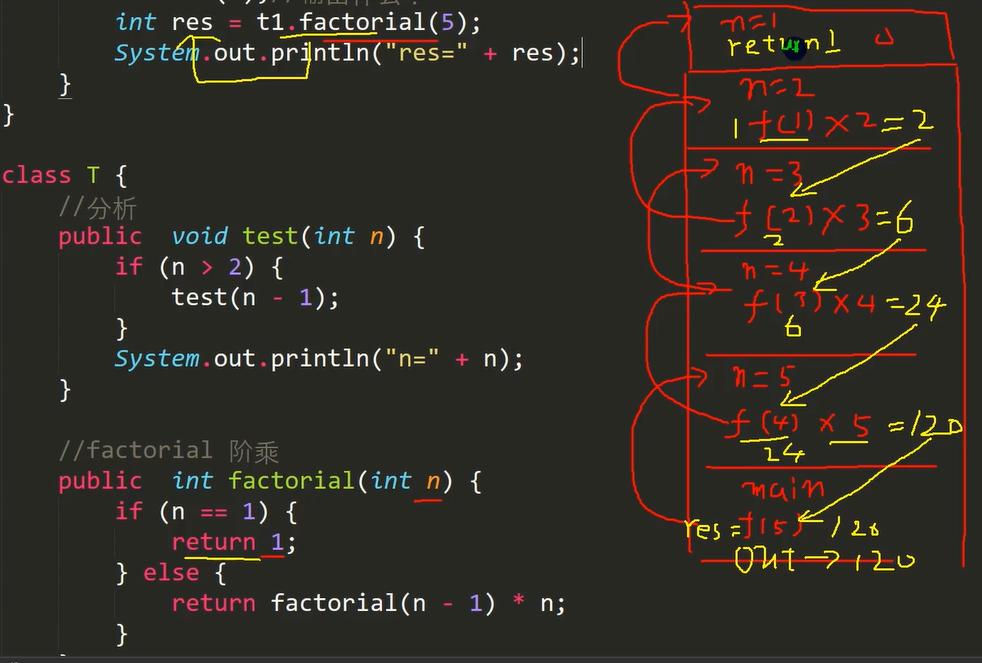
① When a method is executed, a new protected independent space (stack space) is created

② The local variables of the method are independent and will not affect each other

③ If a reference data type (such as array or object) is used in the method, the data of the reference type will be shared

④ Recursion must approach the condition of exiting recursion, otherwise it is infinite recursion

⑤ When a method is executed or returns, it will return. The result will be returned to the person who calls it. At the same time, when the method is executed or returned, the method will also be executed

2, Method overloading

Multiple methods with the same name are allowed in the same class, but the formal parameter list is required to be different

Advantages: it reduces the trouble of naming and registering

matters needing attention:

        Method names must be the same

        The list of formal parameters must be different (the type or number or order of formal parameters, at least one of which is guaranteed to be different, and the parameter name is not required)

        There is no requirement for return type (only different return types do not constitute overloading, but the repeated use of methods)

3, Variable parameters

         JAVA allows you to encapsulate multiple methods with the same name and function but different parameters in the same class into one method, which can be implemented through variable parameters

Basic syntax: access modifier return type method name (data type... Parameter name) {}

//Int... Indicates that variable parameters are accepted, and the type is int, that is, multiple ints (0-many) can be received
//When using variable parameters, it can be used as an array, that is, Num can be used as an array
//Ergodic sum of nums
public int sum(int... nums){
    int res = 0;
    for(int i = 0; i < nums.length; i++){
        res += nums[i];
    }
    return res
}

Details: the arguments of variable parameters can be 0 or any number of arguments

            Arguments to variable parameters can be arrays

            The essence of variable parameters is arrays

            Variable parameters can be placed in the formal parameter list together with common type parameters, but it must be ensured that the variable parameters are at the end

            A formal parameter list can only have one variable parameter

4, Scope

Global variable (attribute): the scope is the whole class body (such as cat class). It can be used directly without assignment. Because there is a default value, it can be used by this class, or by other classes (through object call), and can be decorated

Local variable: variables other than attributes generally refer to variables defined in member methods. The scope is in the code block that defines it. They can only be used after assignment, because there is no default value and can only be used in the corresponding methods in this class without modifiers

Attributes and local variables can have the same name, and access follows the principle of proximity

In the same scope, for example, in the same member method, two local variables cannot have the same name

The life cycle of attributes is relatively long. They are created with the creation of objects and destroyed with the destruction of objects

The life cycle of a local variable is relatively short. It is created with the execution of its code block and destroyed with the end of the code block

5, Constructor (construction method)

Is a special method of a class. Its main function is to complete the initialization of new objects

Basic syntax: [modifier] method name (formal parameter list) {method body;}

Description: constructor has no return value

            Method name and class name must be the same

            The constructor is called by the system (when creating an object, the system will automatically call the constructor of this class to initialize the object)

            A class can define multiple different constructors, that is, constructor overloading

public class Constructor{
    //Write a main method
    public class void main(String[] args){
        //When new an object, specify the name and age directly through the constructor
        //When the constructor is called, the object already exists and just completes initialization
        Person p1 = new Person("smith", 80) //1st constructor
        Person p2 = new Person("tom") //2nd constructor
    }
}

class Person{
    String name;
    int age;
    //1st constructor
    //There is no return value and void cannot be written
    //Constructor name is same as class name
    //String pName, int pAge are formal parameter lists of constructors. The rules are the same as member methods
    public Person(String pName, int pAge){
        name = pName;
        age = pAge;
    }
    //The second constructor only specifies the name, and the default age is 0
    public Person(String pName){
        name = pName;
    }
    //The default parameterless constructor is defined below
    Person(){
    }
}

            If no constructor is defined, the system will automatically generate a default parameterless constructor (also known as the default constructor) for the class: Person() {}   (javap decompile instruction)

            Once you define your own constructor, the default constructor is overwritten. You cannot use the default parameterless constructor unless it is displayed and defined

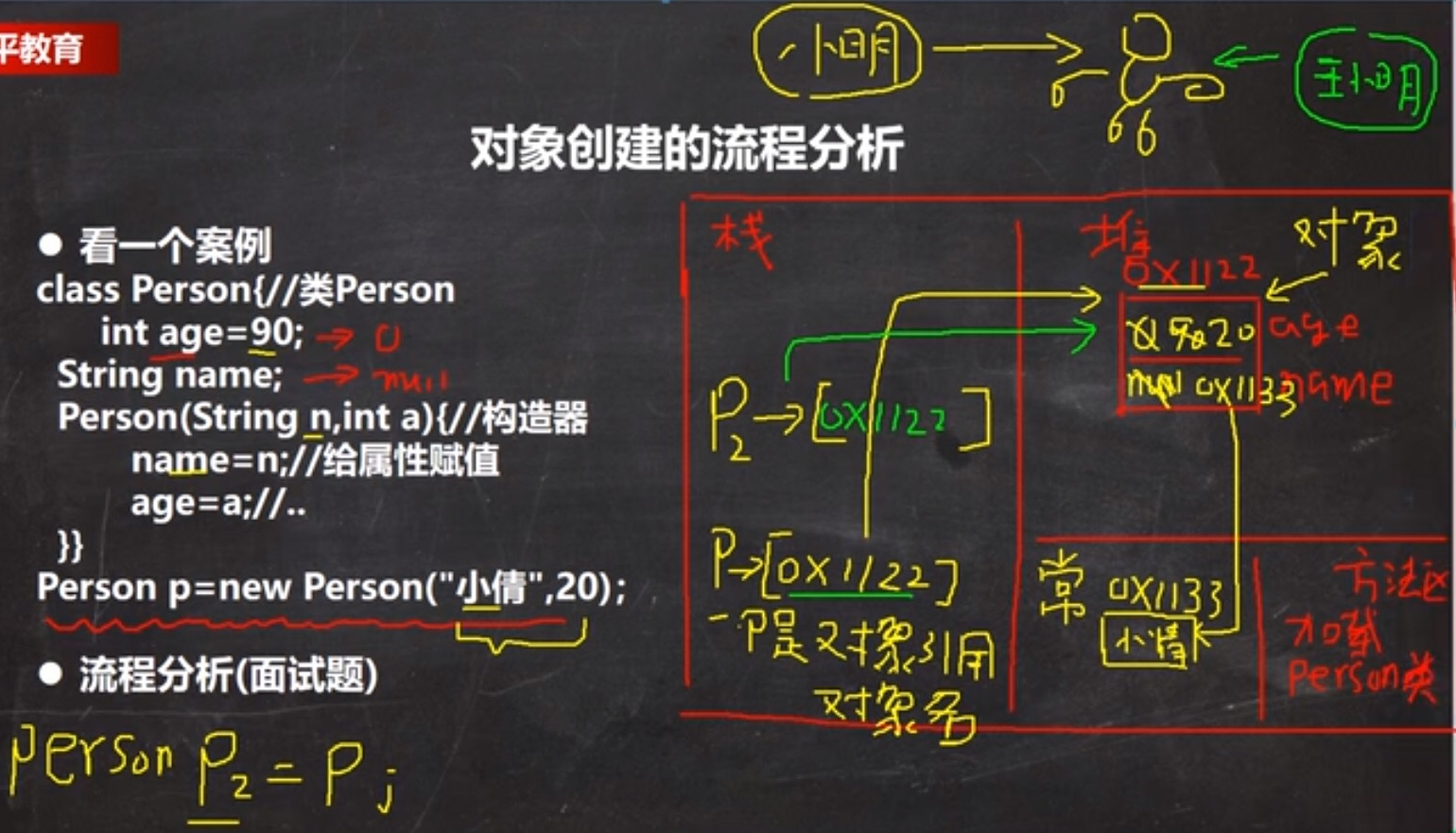
Process analysis for object creation

class Person{
    int age = 90;
    Sttring name;
    Person(String n, int a){
        name = n;
        age = a;
    }
}

Person p = new Person("Xiao Qian", 20);

1. Load the Person class information only once

2. Allocate space (address) in the heap

3. Complete object initialization: default initialization (age = 0, name = null) - > display initialization (age = 90, name = null) - > constructor initialization (age = 20, name = Xiaoqian)

4. Return the address of the object in the heap to p (p is the object name, which can also be understood as the reference of the object)

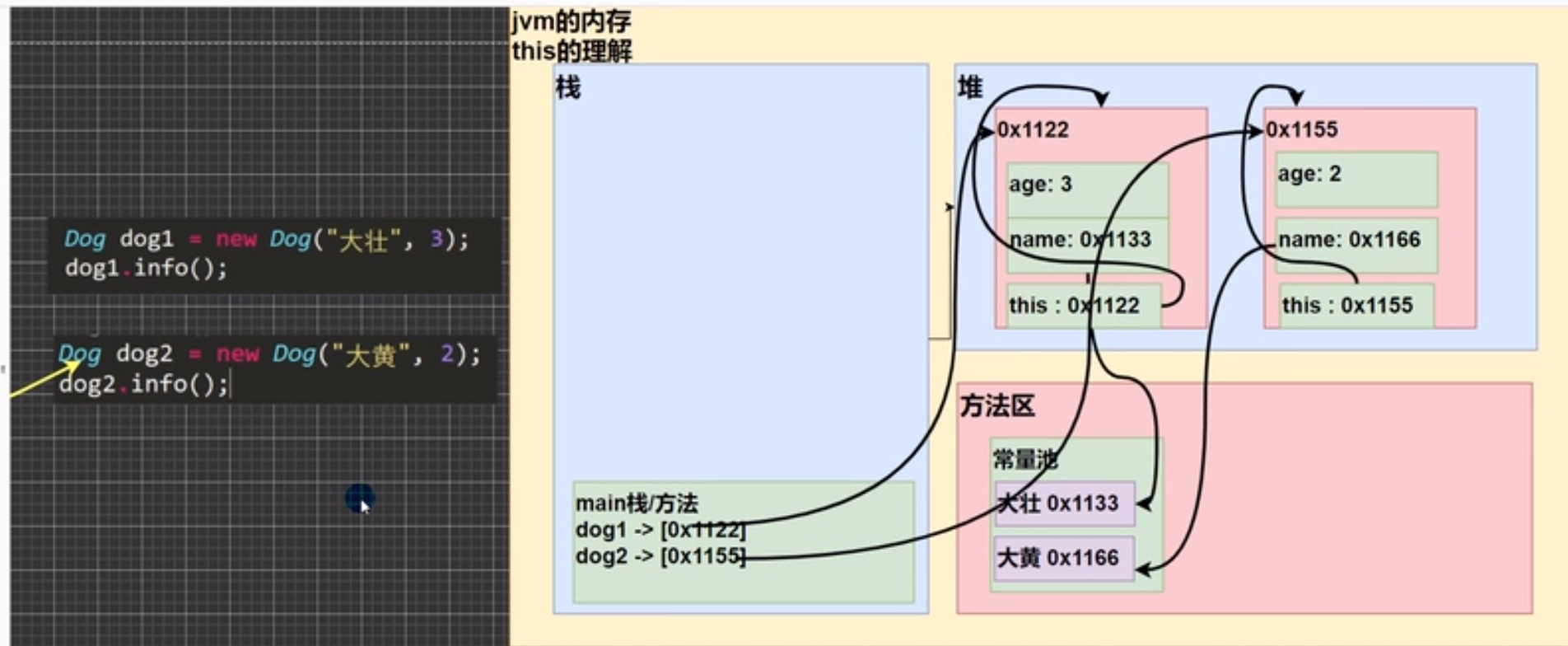
6, this

        This represents the current object (whoever is calling the constructor, this refers to which object)

class Person{
    int age;
    Sttring name;
    
    Person(String name, int age){
        this.name = name;
        this.age = age;
    }
}

Details:

         This keyword can be used to access the properties, methods and constructors of this class

Use in member methods this When you call a property, the result is the property
 However, if a variable with the same name is called directly in a member method, it may be a local variable in the method
 If there is no local variable in the method, it can not be adapted in the method this

         this is used to distinguish between properties and local variables of the current class

         Syntax for accessing member methods: this. Method name (parameter list)

public class Detail{
    public static void main(String[] args){
        T t1 = new T();
        t1.f2();
    }
}

class T{
    //Syntax for accessing member methods: this. Method name (parameter list)
    public void f1(){
        System.out.println("f1()method..");
    }
    public void f2(){
        System.out.println("f2()method..");
        //Call f1 of this class
        //The first way
        f1();
        //The second way
        this.f1();
    }
}


Output:
f2()method..
f1()method..
f1()method..

         Access constructor syntax: this (parameter list) (Note: it can only be used in the constructor and must be placed in the first statement)

public class Detail{
    public static void main(String[] args){
        T t2 = new T();
}

class T{
    //Syntax for accessing constructor: this (parameter list), which can only be used in constructor
    public T(){        
        //Access to T(String name, int age) here must be placed in the first statement
        this("jack", 100);
        System.out.println("T()constructor ");

    }
    public T(String name, int age){
        System.out.println("T(String name, int age)constructor ");
    }
}

Output:
T(String name, int age)constructor 
T()constructor 

         this cannot be used outside the class definition, but only in the method of the class definition

new Test() It is an anonymous object, and the address is not returned, so the object can only be used once
new Test().count() After the anonymous object is created, call count()