Java linked list data structure brush notes summary
This article has referred to the labuladong algorithm, and has compiled some notes and thoughts. You can pay attention to his official account. I'm a vegetable 555. I've just started to brush questions. I'll take notes here. Hey hey~

Characteristics of linked list
Types of linked lists
It is generally divided into one-way linked list, two-way linked list and ring linked list
Characteristics of linked list
- One node chains the next
- Each node contains two parts, one is the value val of the node itself, and the other is the address next pointing to the next node.
- Only sequential access, not random access
- Storage units are not necessarily continuous, and each node can be stored in different locations in memory.
- The length of the linked list is not fixed.
- The efficiency of insertion and deletion is high. Only the pointer change of adjacent nodes needs to be considered, and there is no need to move data. The time complexity is O(1).
- The efficiency of random search is low. It needs to traverse and search one node by one according to the pointer, and the time complexity is O(n).
- Compared with memory, the space consumption of linked list is large, because each node needs to store not only the data itself, but also the address of upper (lower) nodes.
The difference between linked list and array
- Linked list is a chain storage structure; An array is a sequential storage structure.
- Array is a continuous memory area in memory; Linked list is composed of discontinuous memory space;
- The insertion and deletion of elements in the linked list is relatively simple compared with the array, there is no need to move elements, and it is easy to realize length expansion, but it is difficult to find an element;
- The array has strong random access and fast search speed, but the insertion and deletion are complex. Because the maximum length needs to be specified at the beginning of programming, when the maximum length is reached, the expansion length is not as convenient as the linked list, and the memory space requirements are high. There must be enough continuous memory space.
Summary of linked list questions
Common methods for linked list topics:
-
1. Iteration, double pointer. Double pointers (such as fast and slow pointers) are used more, especially when there are two linked lists, ring linked lists, finding and deleting the k-th node.
Typical topics of this kind are:
-
2. Recursion. In fact, many iterations of the linked list can be done by recursion. Although sometimes the complexity may not be as complex as iteration, you can train recursive thinking.
Some skills of linked list problems
-
1. Set pseudo header node
Generally, in order to return the header of a linked list, you need to set a pseudo header node. Because in the iterative process, the pointer will move backward with the iterative process, so there is no way to look forward and return to the head node. Therefore, you can set the pseudo node at the beginning so that the next of the pseudo node points to the head node of the linked list, so that you can return the linked list through dummyHead.next.
//Similar situation ListNode dummyHead = new ListNode(-1); ListNode cur = dummyHead; //...cur.next = ... return dummyHead.next;
-
2. Judge whether there are links in the linked list
If there are links in the linked list, it means that the linked list will return to a previous node to continue the iteration at the end of the iteration. You can use the speed pointer to solve this problem. When the fast pointer is equal to the slow pointer, it means that the fast pointer has an entire ring more than the slow pointer, and there are rings in the linked list; If the fast pointer eventually encounters a null pointer, there is no ring.
Other questions about links in the linked list need to judge whether there are links first.
public boolean hasCycle(ListNode head) { ListNode fast = head, slow = head; while(fast != null){ fast = fast.next.next; slow = slow.next; if(fast == slow) return true; } return false; }Note: when using fast pointers, the loop termination condition should not only write fast= Null and write fast.next= Null, because fast = fast.next.next;
Analysis of hot topics in linked list
206. Reverse linked list (simple)
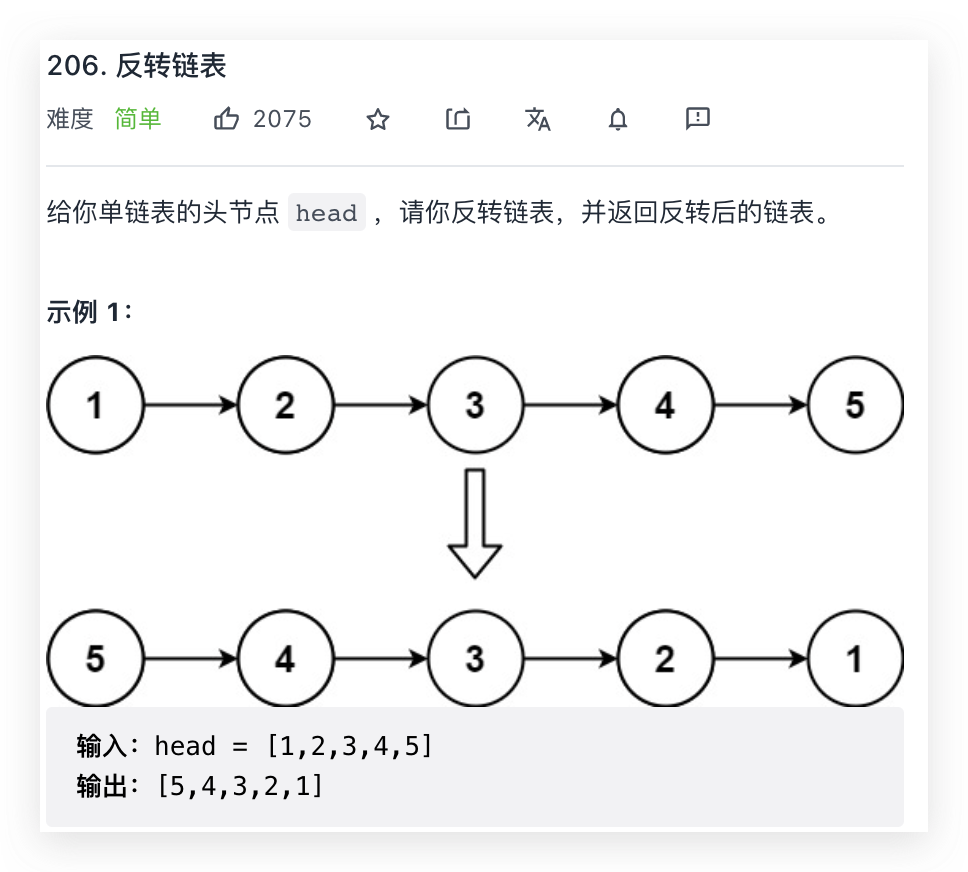
Popular linked list topics are based on this. The meaning of the question is very simple and easy to understand. Two methods can be used: iteration and recursion.
The recursion of linked list is generally tail recursion, that is, recursion to the tail for operation and then continue to operate forward. The recursive problem shows that the problem can be divided into many identical subproblems. When we clarify the same subproblem, we also clarify the definition of the recursive function. For example, the same sub problem of this problem is: * * enter a node, reverse the linked list with this node as the starting point, and return to the head node** Then, suppose we have a linked list 1 → 2 → 3 → 4 → 5. The definition of the function is to reverse the whole linked list, which is equivalent to 1 reversing with reverseList(2 → 3 → 4 → 5), that is, 1 reversing with 5 → 4 → 3 → 2 and returning 5; Then reverseList(2 → 3 → 4 → 5) is equivalent to 2 and reverseList(3 → 4 → 5)... And so on, you can understand the meaning of recursion. When recursing to base case or completing a recursive function, the entry point of the previous recursion will be returned for the operation of the core code.
Note that recursive methods should have a base case as the end point of recursion. In this question, the base case is head.next == null, that is, the last node is recursively passed in. At this time, the next bit of the node is null, so there is no need to reverse with the next bit. At the same time, it is returned as the head node after the inversion of the whole linked list. The next recursive functions return the head node last.
The core operation code of recursive inversion in this problem is head.next.next = head; head.next = null; After the recursive inversion of the linked list, the new head node is last, and the previous head becomes the last node. Don't forget to point to null at the end of the linked list.
When learning recursion, don't jump into recursion to grasp the details, but clarify the definition of recursive function and look at the role of recursion at the overall level.
The iteration of the linked list is intuitive and simple. The previous node needs to be recorded for inversion, and the latter node needs to be recorded for iteration.
//recursion
public ListNode reverseList(ListNode head) {
if(head == null || head.next == null)
return head;
ListNode last = reverseList(head.next);
head.next.next = head;
head.next = null;
return last;
}
//iteration
public ListNode reverseList(ListNode head) {
ListNode pre = null;
while(head != null){
ListNode next = head.next;
head.next = pre;
pre = head;
head = next;
}
return pre;
}
92. Reverse linked list II
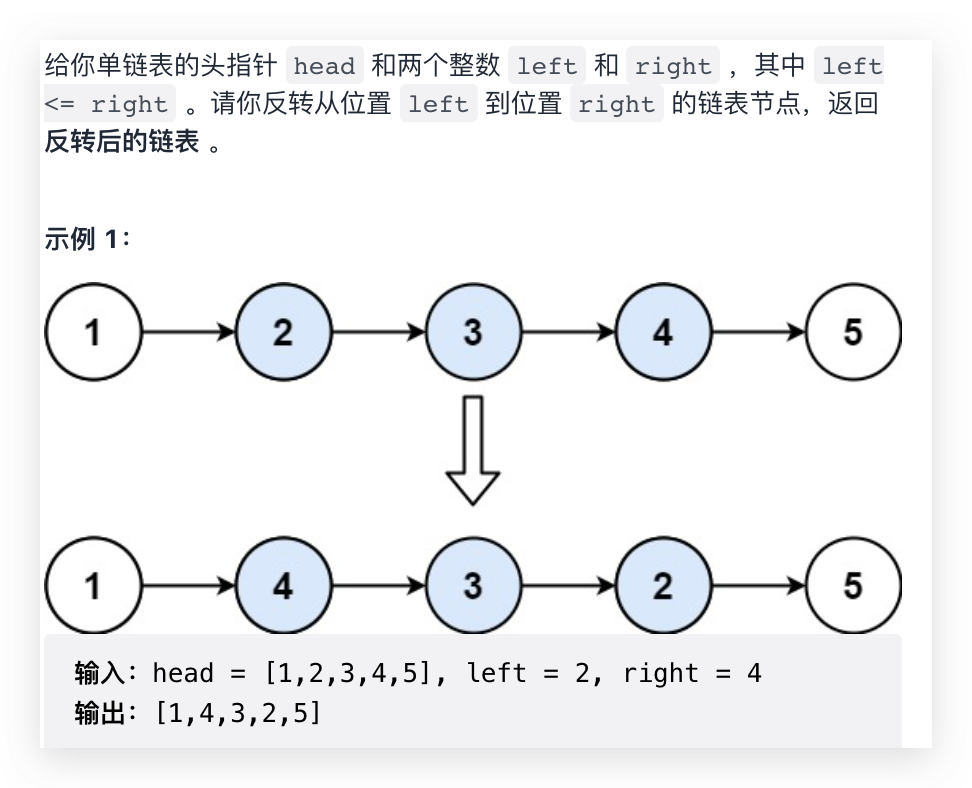
This problem is actually done on the basis of reversing the whole linked list. We just need to convert this problem to reversing the whole linked list. The difference is that it is not reversed from the beginning, so we iterate or recurse to the beginning of the inverted linked list to apply the code of the inverted linked list; In addition, after reversing the linked list, there are still the remaining linked lists. After reversing the linked list, we change from null to the remaining linked list. We only need to record the beginning of the linked list behind the inverted linked list, and then point the inverted linked list to it. The previous question is head.next = null; This question needs to become head.next = next.
Pay special attention when using the iterative method. This is slightly different from the iteration of reversing a whole linked list.
- Locate the head node 2 of the part to be reversed, head = 2; Precursor node 1, pre = 1;
- The next node 3 of the current node is adjusted to the next node 1 - > 3 - > 2 - > 4 - > 5 of the predecessor node,
- The current node is still 2 and the precursor node is still 1. Repeat the previous step...
- 1->4->3->2->5.
//recursion
class Solution {
public ListNode reverseBetween(ListNode head, int left, int right) {
if(left == 1){
head = reverse(head,right);
return head;
}
head.next = reverseBetween(head.next,left-1,right-1);
return head;
}
ListNode next = new ListNode(0);
ListNode reverse(ListNode head, int right){
if(right == 1){
next = head.next;
return head;
}
ListNode last = reverse(head.next,right-1);
head.next.next = head;
head.next = next;
return last;
}
}
//iteration
class Solution {
public ListNode reverseBetween(ListNode head, int left, int right) {
ListNode cur = head;
ListNode pre = new ListNode(0);
pre.next = cur;
for(int i = 1; i < left; i++){
cur = cur.next;
pre = pre.next;
}
for(int i = left; i < right; i++){
ListNode next = cur.next;
cur.next = next.next;
next.next = pre.next;
pre.next = next;
}
return head;
}
}
25. Turn over the linked list in groups of K
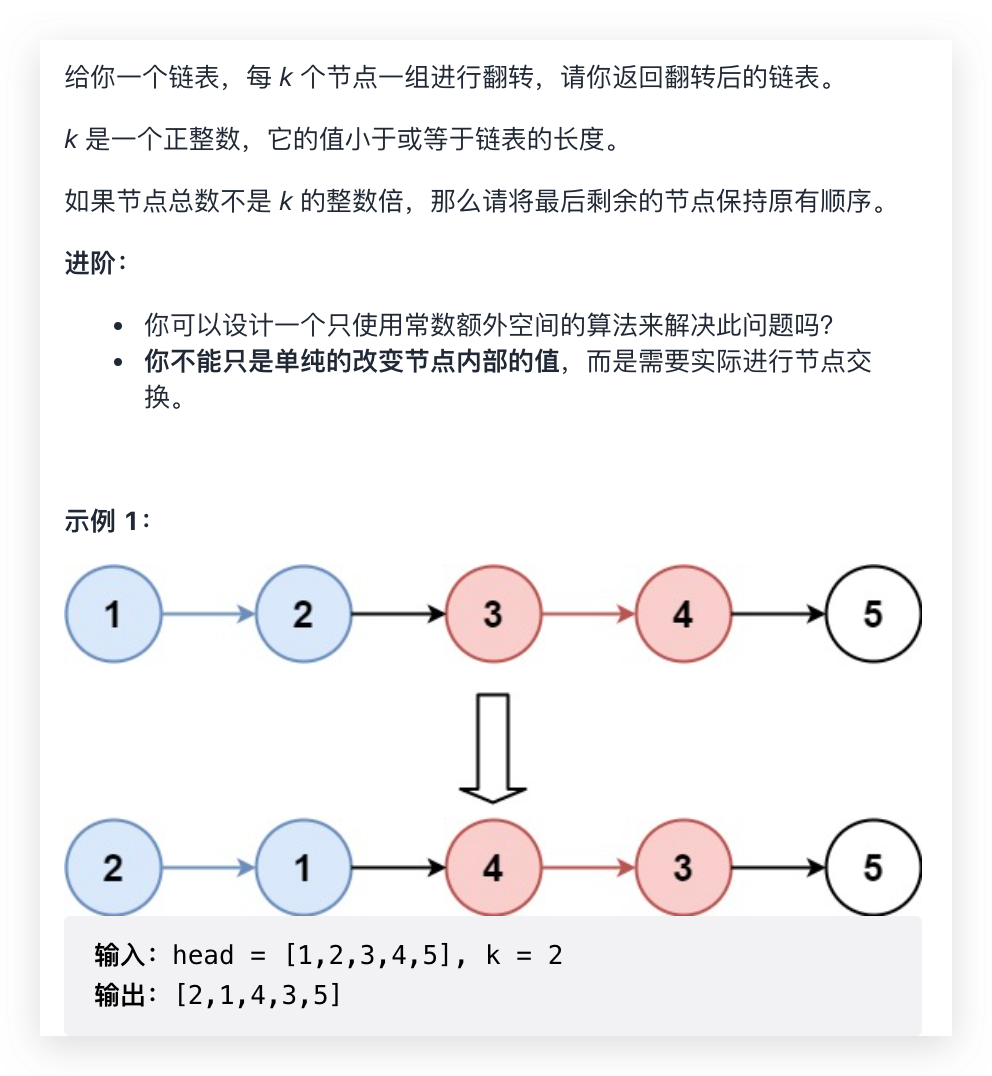
If you have the basis of the above two questions and understand the meaning of recursion, then this problem is not difficult to solve. Just pay attention to a little detail. Let's write down Ben Xiaobai's analysis ideas. If there are mistakes or better ideas, you can point them out~
Let's first look at the topic. If you flip the linked list in groups of K, it can be decomposed into a sub problem. The first k flipped linked lists plus the next K flipped linked lists are the answer - reverse(1 → 2) → reverseKGroup(3 → 4 → 5), that is, recursion can be used.
Then, after clarifying the general idea of recursion, we can define our base case. Here, there are two base cases of recursive methods. One is just divisible, so the recursive head to the bottom layer is null, and null can be returned; The other is not divisible. For example, if there is a 5 left in this example, cur == null will appear when 5 loops to the next k. This section does not need to be reversed. Then it is good to directly return the section without inversion, that is, the original head. That is, first judge whether its length is greater than or equal to k. If so, we will flip this part of the linked list, otherwise we don't need to flip it.
If you have a base case, go back to those layers that need to be reversed. Each layer is equivalent to the first k layers to be reversed, and then link to the following linked list to continue to reverse the first k layers. For example, after the bottom layer 5 returns, the current head is 3 - > 4 - > 5. After reversing the first k, it becomes 4 - > 3 - > 5, and so on. That is, each layer returns the inverted head, and the previous layer links this layer, that is, the return of the next link of the last number of the previous layer.
After clarifying the idea, the rest is the details. For example, you need to save each group of head nodes and tail nodes, and how to enter the recursive connection to the next group. I believe you can understand these by looking at the code.
Iterative method
Can refer to Official explanation
//recursion
class Solution {
public ListNode reverseKGroup(ListNode head, int k) {
if(head == null) //Just k base case s return null
return null;
ListNode pre = new ListNode(-1);
ListNode cur = head;
pre.next = cur;
for(int i = 0; i < k; i++){
if(cur == null) //If it is less than k, it will directly return to the head node, and there is no need to reverse it
return head;
cur = cur.next;
pre = pre.next; //Iterate to the last of the group first
}
pre.next = reverseKGroup(cur,k); //The last node of this group is connected to the head node of the next group
return reverseN(head,k); //Invert the first k nodes of this group and return the head node
}
ListNode next = new ListNode(0);
ListNode reverseN(ListNode head, int k){
if(k == 1){
next = head.next;
return head;
}
ListNode last = reverseN(head.next,k-1);
head.next.next = head;
head.next = next;
return last;
}
}
//iteration
class Solution {
public ListNode reverseKGroup(ListNode head, int k) {
ListNode hair = new ListNode(0);
hair.next = head;
ListNode pre = hair;
while (head != null) {
ListNode tail = pre;
// Check whether the length of the remaining part is greater than or equal to k
for (int i = 0; i < k; ++i) {
tail = tail.next;
if (tail == null) {
return hair.next;
}
}
ListNode nex = tail.next;
ListNode[] reverse = myReverse(head, tail);
head = reverse[0];
tail = reverse[1];
// Reconnect the sub linked list to the original linked list
pre.next = head;
tail.next = nex;
pre = tail;
head = tail.next;
}
return hair.next;
}
public ListNode[] myReverse(ListNode head, ListNode tail) {
ListNode prev = tail.next;
ListNode p = head;
while (prev != tail) {
ListNode nex = p.next;
p.next = prev;
prev = p;
p = nex;
}
return new ListNode[]{tail, head};
}
}
24. Exchange the nodes in the linked list

After learning the previous question, you will find that this question is really a small case, because this question is equivalent to k=2 of the previous question. Although the idea is the same, our code can be much simpler. Just look at the notes here.
//recursion
class Solution {
public ListNode swapPairs(ListNode head) {
if (head == null || head.next == null) { //Divisible or non divisible cases are included
return head;
}
ListNode last = head.next; //Record the last node of the group
head.next = swapPairs(last.next); //Exchange the next group, and connect the original head node of this group with the head node returned by the next group
last.next= head; //Both lines of code are exchanged
return last; //Returns the header node of this group
}
}
//iteration
class Solution {
public ListNode swapPairs(ListNode head) {
ListNode dummyHead = new ListNode(0);
dummyHead.next = head;
ListNode temp = dummyHead;
while (temp.next != null && temp.next.next != null) {
ListNode node1 = temp.next;
ListNode node2 = temp.next.next;
temp.next = node2;
node1.next = node2.next;
node2.next = node1;
temp = node1;
}
return dummyHead.next;
}
}
143. Rearrange the linked list

This problem is also done on the basis of the above problems. Basically, we can complete this problem by finding out the law of the problem. It is not difficult. Note that the target linked list is the result of combining the left half of the original linked list with the right half after inversion. Therefore, we only need to use the double pointer technique to find the midpoint, use the reverse linked list technique to reverse the following linked list, and then use the double pointer technique to merge the two linked lists.
class Solution {
public void reorderList(ListNode head) {
// Find the midpoint
ListNode fast = head, slow = head;
while(fast != null && fast.next != null){
fast = fast.next.next;
slow = slow.next;
}
// Linked list after reversing the midpoint
ListNode midHead = slow.next;
slow.next = null; //Remember to set the midpoint of the first chain to null, otherwise there will be rings after the merger
ListNode pre = null;
while(midHead != null){
ListNode next = midHead.next;
midHead.next = pre;
pre = midHead;
midHead = next;
}
// Merge two linked lists
ListNode next1;
ListNode next2;
ListNode cur1 = head;
ListNode cur2 = pre;
while(cur1 != null && cur2 != null){
next1 = cur1.next;
next2 = cur2.next;
cur1.next = cur2;
cur1 = next1;
cur2.next = cur1;
cur2 = next2;
}
}
}
summary
The linked list problem is relatively simple on the whole. After fully understanding the characteristics of the linked list, it can be used as the first choice for novices to brush the data structure. Through the linked list, we can learn about recursion, decomposition problems and some ideas in-depth layers, such as reversing the linked list → reversing a part of the linked list → reversing k linked lists. From the simple to the deep, we can cultivate our problem-making thinking. If we directly reverse k linked lists, it will be more difficult, but if we do the first two simple questions, it will be suddenly enlightened.
At present, the author is still in the stage of just starting to brush questions, so many codes are not written very beautiful or concise enough, or I won't have more efficient algorithms. You can point them out directly and teach me by the way, hahaha~