1. Depth First Traversal (DFS)

depth first search (DFS) is an extension of precedence traversal. We start with a vertex A and then recursively traverse all vertices adjacent to A node. When accessing a vertex A, since we had reached that point at that time, we could mark that point as visited, and recursively call DFS for all adjacent vertices that have not been marked.

Simply put: DFS is to first reach the longest path that the current traversal path can reach, once the end of the path is reached, then retrospect, and start the traversal of the new branch path from the original traversed vertex.

                                                                       

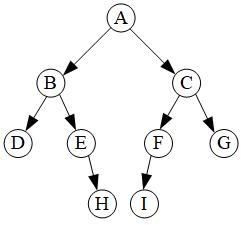
Depth first traverses each node, requiring the use of the Stack data structure. Stack is characterized by first-in-first-out, first pressing the right node into the stack, and then pressing the left node into the stack, so that the stack order is first left node and then right node.

The whole traversal process is as follows: First, the A node is pushed into the stack (A);

The A node is popped up and the sub-nodes C and B of A are pushed into the stack. At this time, B is at the top of the stack, stack(B,C).

The B node is ejected and the sub-nodes E and D of B are pushed into the stack. At this time D is at the top of the stack, stack (D,E,C).

Pop up the D node, because D has no sub-nodes to press in, then E is at the top of the stack, stack (E, C);

The E node is ejected and the sub-node H of E is pressed into stack (H,C).

The H node pops up, because H has no sub-nodes to press in, then C is at the top of the stack, while C's G, F sub-nodes are pushed into the stack, stack (C, F, G);

The traversal results are: A, B, D, E, H, C, F, I, G.

(1) Non-recursive code is implemented as follows:

/*
public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;

    public TreeNode(int val) {
        this.val = val;

    }
}
*/

public class Main1 {
    public ArrayList<Integer> DfsTree(TreeNode root) {
        ArrayList<Integer> lists = new ArrayList<I>();
        if(root == null)
            return lists;
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while(!stack.isEmpty()){
            TreeNode tree = stack.pop();
　　　　　　//Press the right node in the stack first, then the left node, and then the left node out of the stack is the left node first and then the right node.
            if(tree.right != null)
                stack.push(tree.right);
            if(tree.left != null)
                stack.push(tree.left);
            lists.add(tree.val);
        }
        return lists;
    }
}

(2) Recursive code implements DFS as follows:

      
private void DfsRecursive(TreeNode root){ 
 
     if (root != null)   
    {  
       System.out.print(root.value+"  ");  
       DfsRecursive(root.left);  
       DfsRecursive(root.right);  
    }         
}

2. breadth-first traversal (BFS)

The basic operation of breadth-first search is similar to depth-first search, but here it is realized by queue, finding a starting point A, and putting the points adjacent to A into the queue. At this time, the first element B of the queue is taken out, and the points adjacent to B that have not been visited are put into the queue, and this operation is repeated continuously until the queue is empty. At this time, the vertices visited sequentially are traversing. Sequence.

                                                                  

The breadth-first traversal tree needs to use queues to store node objects. The characteristics of queues are first-in, first-out. First insert the left node into the Queue, then insert the right node, the Queue is first out of the left node, then out of the right node.

Firstly, the A node is inserted into the queue with elements (A).

A node is ejected, and the left node B and right node C of A node are inserted into the queue in turn. B is at the head of the queue and C is at the end of the queue. (B, C) At this time, A node is obtained.

The first element B is popped up, and the left node D and the right node E of B are inserted into the queue. C is at the head of the queue and E is at the end of the queue (C, D, E), then the B node is obtained.

Then the first element C is popped up, and the left node F and the right node G of the C node are inserted into the queue in turn, (D, E, F, G), then the C node is obtained.

When D pops up, D has no sub-nodes, and the elements in the queue are (E, F, G) to get the D-nodes.

. And so on. The final traversal results are: A, B, C, D, E, F, G, H, I.

/*
public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;

    public TreeNode(int val) {
        this.val = val;

    }

}
*/

public class Main2{
    public ArrayList<Integer> BfsTree(TreeNode root) {
        ArrayList<Integer> lists = new ArrayList<>();
        if(root == null)
            return lists;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while(!queue.isEmpty()){
            TreeNode tree = queue.poll();
            if(tree.left != null)
                queue.offer(tree.left);
            if(tree.right != null)
                queue.offer(tree.right);
            lists.add(tree.val);
        }
        return lists;
    }
}