14.9 Freudian algorithm

14.9.1 introduction to Floyd algorithm

1. Like Dijkstra algorithm, Floyd algorithm is also an algorithm for finding the shortest path between vertices in a given weighted graph. The algorithm is named after Robert Freud, one of the founders, the winner of the Turing prize in 1978 and professor of computer science at Stanford University
2. Floyd algorithm calculates the shortest path between the vertices in the graph
3. Dijestra algorithm is used to calculate the shortest path from a vertex to other vertices in the graph.
4. Freud algorithm VS dijestra algorithm: dijestra algorithm finds the shortest path from the starting access vertex to other vertices through the selected accessed vertices; Every vertex in Freud's algorithm is the starting access point, so we need to treat each vertex as the accessed vertex and find the shortest path from each vertex to other vertices.

14.9.2 graphical analysis of Floyd algorithm

1. If the shortest path from vertex vi to vertex vk is known as Lik, the shortest path from vertex vk to vj is known as Lkj, and the path from vertex vi to vj is Lij, then the shortest path from vi to vj is: min((Lik+Lkj),Lij), and the value of vk is all vertices in the graph, then the shortest path from vi to vj can be obtained
2. The shortest path Lik from vi to vk or the shortest path Lkj from vk to vj is obtained in the same way
3. Graphic analysis of Floyd algorithm -- Examples

Example: Taking the shortest path as an example

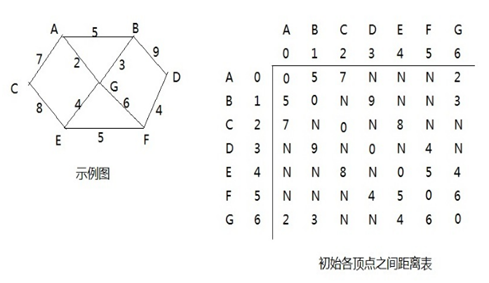
Steps of Freudian algorithm:
In the first cycle, take A (subscript: 0) as the intermediate vertex [that is, traverse all cases where A is the intermediate vertex to obtain the updated distance table and precursor relationship], and the distance table and precursor relationship are updated as follows:

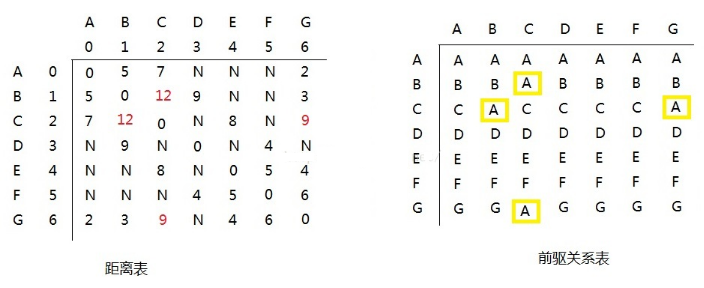
The analysis is as follows:

1. With vertex a as the middle vertex, the distance between B - > A - > C is from n - > 9, similarly, C to B; The distance between C - > A - > G is from n - > 12, similarly, G to C
2. Replace the middle vertex and cycle the operation until all vertices are updated as middle vertices, and the calculation ends

Next, we solve the shortest path problem

14.9.3 best application of Floyd algorithm - shortest path

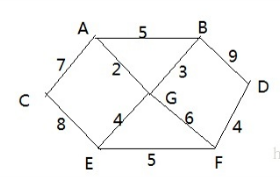
1. There are 7 villages (A, B, C, D, E, F, G) in Shengli township
2. The distance of each village is indicated by A sideline (right of way), for example, A – B is 5km away
3. Q: how to calculate the shortest distance from each village to other villages?
4. code implementation

import java.util.Arrays;
/**
 * @author zk
 * @version 1.0.0
 * @ClassName FloydAlgorithm.java
 * @Description TODO Freudian algorithm -- find the minimum distance from each vertex to each other
 * @createTime 2021 October 3, 2015 15:03:00
 */
public class FloydAlgorithm {
    public static void main(String[] args) {
        // Test to see if the diagram is created successfully
        char[] vertex = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
        //Create adjacency matrix
        int[][] matrix = new int[vertex.length][vertex.length];
        final int N = 65535;
        matrix[0] = new int[] { 0, 5, 7, N, N, N, 2 };
        matrix[1] = new int[] { 5, 0, N, 9, N, N, 3 };
        matrix[2] = new int[] { 7, N, 0, N, 8, N, N };
        matrix[3] = new int[] { N, 9, N, 0, N, 4, N };
        matrix[4] = new int[] { N, N, 8, N, 0, 5, 4 };
        matrix[5] = new int[] { N, N, N, 4, 5, 0, 6 };
        matrix[6] = new int[] { 2, 3, N, N, 4, 6, 0 };
        Graph graph = new Graph(matrix, vertex);
        graph.floyd();
        graph.show();
    }
}
class Graph{
    private char[] vertex; // Save individual vertices
    private int[][] dis; // Save the distance from each vertex to other vertices, and the final result is also saved in the array
    private int[][] pre; // Saves the precursor vertex that reached the target vertex
    // constructor 
    public Graph(int[][] dis,char[] vertex){
        int length = vertex.length;
        this.vertex = vertex;
        this.dis = dis;
        this.pre = new int[length][length];
        for (int i = 0; i < length; i++) {
            Arrays.fill(this.pre[i],i);
        }
    }

    // Freudian algorithm is easy to understand and easy to implement
    public void floyd(){
        int len = 0; //Variable save distance
        //Traversing the middle vertex, k is the subscript of the middle vertex [A, B, C, D, E,G]
        for (int k = 0; k < dis.length; k++) {
            //Starting from vertex i [A, B, C, D, E,G]
            for (int i = 0; i < dis.length; i++) {
                //Reach j vertex / / [A, B, C, D,E,G]
                for (int j = 0; j < dis.length; j++) {
                    len = dis[i][k] + dis[k][j]; // =>Find the distance from vertex i to vertex j after passing through the middle vertex of k
                    if (len<dis[i][j]){ // If len is less than dis[i][j]
                        dis[i][j] = len; // Update distance
                        pre[i][j] = pre[k][j]; // Update precursor vertices
                    }
                }
            }
        }

    }
    
    // Display pre array and dis array
    public void show(){
        for (int i = 0; i < dis.length; i++) {
            // First output a row of the pre array
            for (int j = 0; j < pre.length; j++) {
                System.out.print(vertex[pre[i][j]] + " ");
            }
            System.out.println();

            // Output a row of data of dis array
            for (int j = 0; j < dis.length; j++) {
                System.out.print(vertex[i]+"reach"+vertex[j]+"The shortest path for is"+dis[i][j] + " ");
            }
            System.out.println();
        }
        
        
    }
}