Tree structure is a very important structure in data structure. Tree is widely used in file storage, index implementation and data search. The tree's level traversal, pre order traversal, middle order traversal and post order traversal all need us to be very familiar with. For people like me, the tree's traversal was always very simple, and several lines of code were written in the recursive way. Then when it was required to use the non recursive way for pre order, middle order and post order traversal, we only knew to use the stack to realize it, just yesterday. I used to think non recursive implementation was not so difficult, and then when I really started to write, I knew it was not so simple. So after realizing these recursive and non recursive methods, I write this article, which provides you with some ideas and a summary of your own learning traversal!

1. Preamble traversal:

First, code:

    //Recursive preorder traversal
    public void preScanIt(TreeNode node){
        if (node == null){
            return;
        }
        System.out.print(node.val+" ");
        preScanIt(node.leftChild);
        preScanIt(node.rightChild);
    }
        //Non recursive preorder traversal
    public void preScan(TreeNode node){
        Stack<TreeNode> stack = new Stack<>();
        stack.add(node);
        while (!stack.isEmpty()){
            TreeNode temp = stack.pop();
            System.out.print(temp.val+" ");//Each time you visit the left and right nodes of a node, you need to output (or store) the value of the node in the final result.
            if (temp.rightChild != null){
                stack.add(temp.rightChild);
            }
            if (temp.leftChild != null){
                stack.add(temp.leftChild);
            }
        }
    }

Preorder traversal is relatively simple, because it accesses the parent node first, then the left and right child nodes. In the recursive mode, we only need to save the parent node in the traversal result sequence before each recursive visit to the left and right children. In the non recursive way, stack is used to store node values. At this time, the pre order traversal is simpler than the mid order and post order traversal, because it only needs to take one node out of the stack each time, output the node content, and then add its child nodes into the stack according to the left and right first.

2. Middle order traversal

    //Recursive middle order traversal
    public void midScanIt(TreeNode node){
        if (node == null){
            return;
        }
        midScanIt(node.leftChild);
        System.out.print(node.val+" ");
        midScanIt(node.rightChild);
    }

    //Non recursive middle order traversal
    public void midScan(TreeNode node){
        Stack<TreeNode> stack = new Stack<>();
        TreeNode p = node;

        while (!stack.isEmpty() || p != null){
            if(p != null){//Access all left nodes first
                stack.add(p);
                p = p.leftChild;
            }else {
                p = stack.pop();//If the left node is empty, or the left node has been traversed, the node value is output.
                System.out.print(p.val+" ");
                p = p.rightChild;//Then access the right node
            }
        }
    }

The recursive traversal of post order traversal is very simple.
I think the idea of non recursive traversal is very important. I can learn it.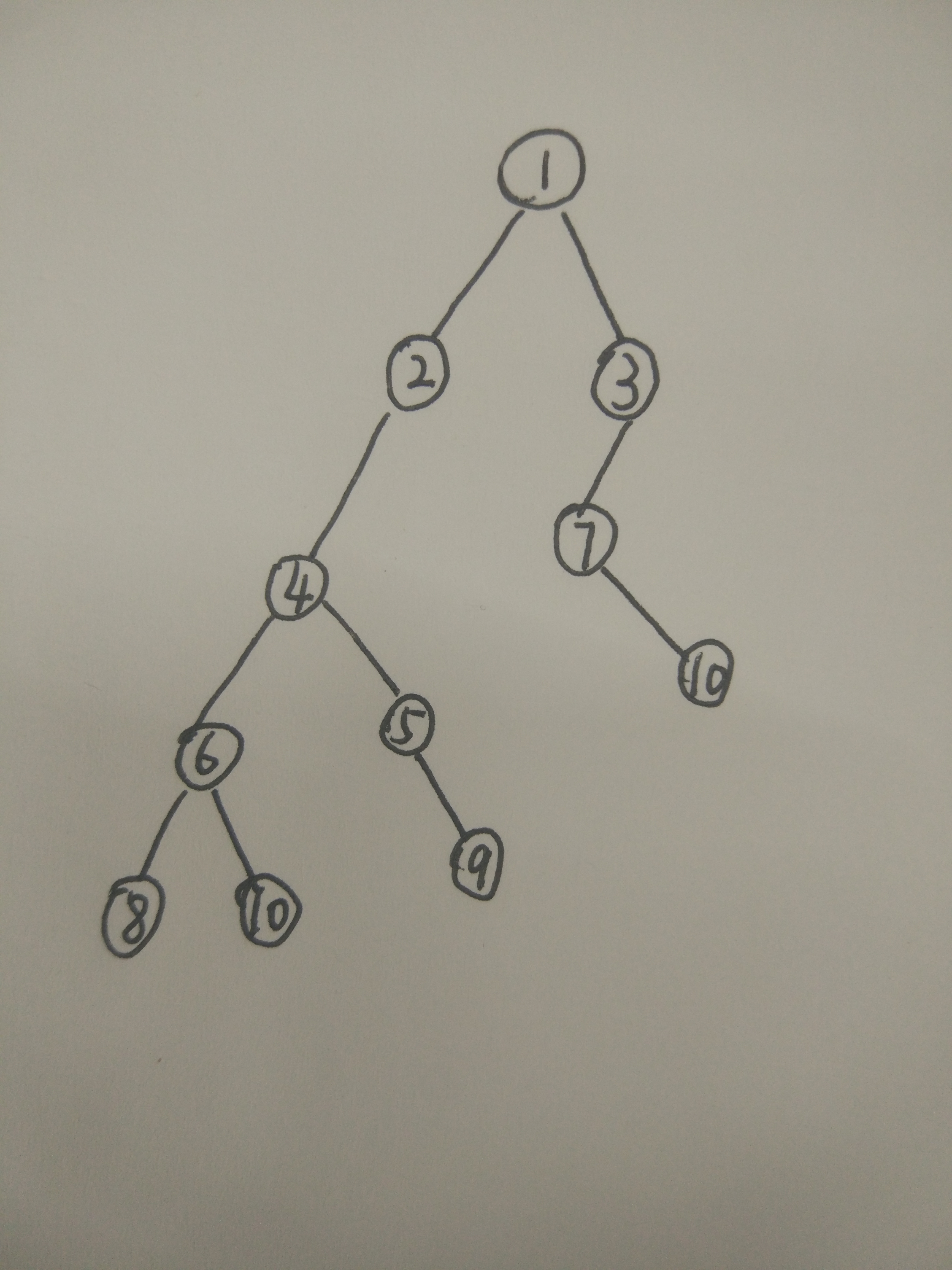

Now take a tree as an example to illustrate the steps of non recursive traversal:

Step i	Content in stack	Current node p points to	Output sequence
0	null	Node (root node)
1	1	2
2	1,2	4
3	1,2,4	6
4	1,2,4,6	8
5	1,2,4,6,8	Null (left child of 8)
6	1,2,4,6	Null (right child of 8)	8
7	1,2,4	10 (right child of 6)	8，6
8	1,2,4,10	null	8，6
9	1,2,4	null	8，6，10
10	1,2	5 (right child of 4)	8，6，10，4
11	1,2,5	Null (left child of 5)	8，6，10，4
12	1,2	9 (left child of 5)	8，6，10，4，5
13	1,2，9	null (left child of 9)	8，6，10，4，5
14	1,2	null (right child of 9)	8，6，10，4，5，9
15	1	Null (right child of 2)	8，6，10，4，5，9，2
16	null	3 (right child of 1)	8，6，10，4，5，9，2 ,1
17	3	7	8，6，10，4，5，9，2 ，1
18	3，7	Null (left child of 7)	8，6，10，4，5，9，2，1
19	3	10 (left child of 7)	8，6，10，4，5，9，2，1，7
20	3，10	Null (left child of 10)	8，6，10，4，5，9，2，1，7
21	3	Null (right child of 10)	8，6，10，4，5，9，2，1，7 ，10
22	null	Null (right child of 3)	8，6，10，4，5，9，2，1，7，10，3

This traversal method has a good idea and can be used to solve many problems related to trees.

3. Post order traversal

    //Recursive subsequent traversal
    public void nextScanIt(TreeNode node){
        if (node == null){
            return;
        }
        nextScanIt(node.leftChild);
        nextScanIt(node.rightChild);
        System.out.print(node.val+" ");
    }

      //Non recursive postorder traversal
    public void nextScan(TreeNode node){
        //Mark whether to return from left or right subtree
        Stack<Boolean> flag = new Stack<>();
        //Storage node
        Stack<TreeNode> stack = new Stack<>();
        TreeNode p = node;
        while (!stack.isEmpty() || p != null){
            if (p != null){
                stack.add(p);
                p = p.leftChild;
                flag.add(false);//Mark in left subtree
            }else {
                if (flag.pop()){//Return from the right subtree, that is, the previous node is the right subtree of the node to be accessed
                    p = stack.pop();
                    System.out.print(p.val+" ");
                    p = null;//The best way here is to set it to 0, because the subtree with p as the node has been traversed, and this tree does not know whether it is the left subtree or the right subtree of the previous node.
                }else {//Return from the left subtree. When the left subtree returns, it cannot output a node. First, access its right child.
                    p = stack.peek();
                    p = p.rightChild;
                    flag.add(true);
                }
            }
        }
    }

The idea of post order traversal is almost the same as that of middle order traversal, except that a flag is added to indicate whether the node currently pointed to is the left child or the right child node of the parent node. If it is returned from the left child node, then the parent node will not be operated to access the right child node of the father first; if it is returned from the right child node, then the value of the node will be output directly.

4. Hierarchical traversal

The hierarchical traversal is different from the pre order, middle order and post order traversal, and it adopts the way of queue to traverse.

    //level traversal
    public void levelScan(TreeNode node){
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(node);
        while (!queue.isEmpty()){
            TreeNode temp = queue.poll();
            System.out.print(temp.val + " ");
            if (temp.leftChild != null){//If the left child is not empty, join the queue
                queue.add(temp.leftChild);
            }
            if (temp.rightChild != null){//If the child is not empty, join the queue
                queue.add(temp.rightChild);
            }

        }
    }

Test procedure:

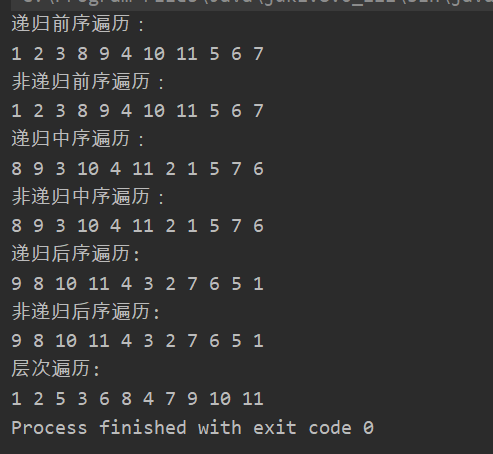
 public static void main(String[] args) {
        ScanTree scanTree = new ScanTree();
        TreeNode t1 = new TreeNode(1);
        TreeNode t2 = new TreeNode(2);
        TreeNode t3 = new TreeNode(3);
        TreeNode t4 = new TreeNode(4);
        TreeNode t5 = new TreeNode(5);
        TreeNode t6 = new TreeNode(6);
        TreeNode t7 = new TreeNode(7);
        TreeNode t8 = new TreeNode(8);
        TreeNode t9 = new TreeNode(9);
        TreeNode t10 = new TreeNode(10);
        TreeNode t11 = new TreeNode(11);
        t1.leftChild = t2;
        t1.rightChild = t5;
        t2.leftChild = t3;
        t3.leftChild = t8;
        t8.rightChild = t9;
        t3.rightChild = t4;
        t4.leftChild = t10;
        t4.rightChild = t11;
        t5.rightChild = t6;
        t6.leftChild = t7;
        System.out.println("Recursive preamble traversal:");
        scanTree.preScanIt(t1);
        System.out.println("\n Non recursive preamble traversal:");
        scanTree.preScan(t1);
        System.out.println("\n Recursive middle order traversal:");
        scanTree.midScanIt(t1);
        System.out.println("\n Non recursive middle order traversal:");
        scanTree.midScan(t1);
        System.out.println("\n Recursive postorder traversal:");
        scanTree.nextScanIt(t1);
        System.out.println("\n Non recursive postorder traversal:");
        scanTree.nextScan(t1);
        System.out.println("\n level traversal:");
        scanTree.levelScan(t1);

    }

Result: