1. piles
- Two fork pile
Binary heap is a complete binary tree (different from full binary tree)
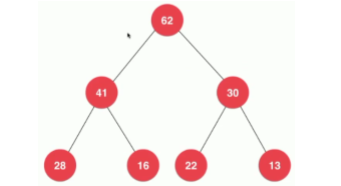
The value of a node in the heap is always no greater than the value of its parent node

Generally, this kind of heap is called the maximum heap (the corresponding minimum heap can be defined)
An element in the lower layer is not necessarily smaller than an element in the upper layer
Since it is a complete binary tree, you can define the structure with an array
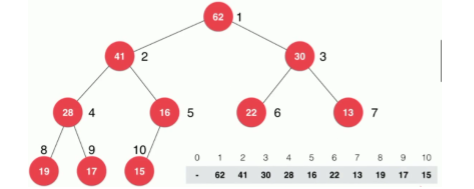
The structure is stored in the array, where the father of any node has the following logical relationship with the left and right children
When the corner of the root node is 1
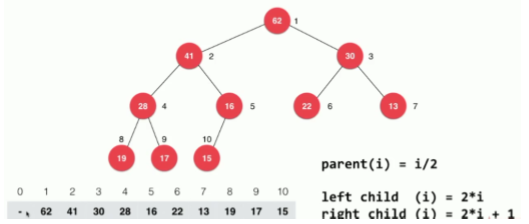
When the angle of the root node is 0
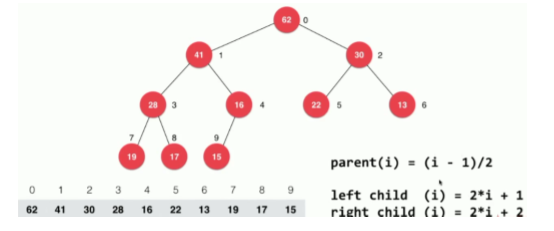
- code implementation
package Heap and priority queues;
import Dynamic array.ArrayList;
//Maximum heap / minimum heap based on array
public class MaxHeap<E extends Comparable<E>> {
private ArrayList<E> data;
public MaxHeap() {
data=new ArrayList<>();
}
public MaxHeap(int capacity){
data=new ArrayList<>(capacity);
}
//Heap: heap any array
public MaxHeap(E[] arr){
data=new ArrayList<>(arr);
for(int i=parent(data.getSize()-1);i>=0;i--){
siftDown(i);
}
}
//Returns the number of elements in the heap
public int size(){
return data.getSize();
}
//Determine if the heap is empty
public boolean isEmpty(){
return data.isEmpty();
}
//Three auxiliary functions
//Get the corner sign of the parent node
private int parent(int index){
if(index==0){
throw new IllegalArgumentException("No parent node");
}
return (index-1)/2;
}
//Get the corner sign of the left child node
private int leftChild(int index){
return 2*index+1;
}
//Get the corner sign of the right child node
private int rightChild(int index){
return 2*index+2;
}
//Add an element
public void add(E e){
data.addLast(e);
siftUp(data.getSize()-1);
}
//Element float up operation
private void siftUp(int index) {
//If index > 0 is root, there is no parent node, and the parent node is smaller than itself
while(index>0&&data.get(parent(index)).compareTo(data.get(index))<0){
data.swap(index, parent(index));
index=parent(index);
}
}
//View maximum in heap
public E findMax(){
if(data.isEmpty()){
throw new IllegalArgumentException("Heap empty");
}
return data.getFirst();
}
//Delete maximum in heap
public E extraMax(){
E e=findMax();
data.swap(0, data.getSize()-1);
data.removeLast();
siftDown(0);
return e;
}
//Sinking operation
private void siftDown(int index) {
//Just compare the value of left and right children, which one is bigger
while(leftChild(index)<data.getSize()){//Left child doesn't cross the border
//If there is no right child or there is a right child, but the value of the right child is smaller than the value of the left child, then k means the coordinate is the value of the left child
int k=leftChild(index);
//There are right children, and right children are older than left children
if(k+1<data.getSize()&&data.get(k+1).compareTo(data.get(k))>0){
//Because the right child's value is greater than the left child's, k stores the right child's corner sign
k=rightChild(index);
//At this time, data[k] is the maximum value of leftChild and rightChild
}
if(data.get(index).compareTo(data.get(k))<0){
data.swap(index, k);
index=k;
}else{
break;
}
}
}
//Take out the original maximum value and replace the new value
public E replace(E e){
E res=findMax();
data.set(0, e);
siftDown(0);
return res;
}
public void clear(){
data.clear();
}
}