Sequential search

Find in the order of the array

package bilibili.search;

public class SeqSearch {
    public static void main(String[] args) {
        int[] array = {1,3,23,45,67,-6,12};
        int index = Search(array,45);
        System.out.println("Subscript is: " + index);
    }
    public static int Search(int[] array,int values){
        for (int i = 0; i < array.length; i++) {
            if(array[i]==values){
                return i;
            }
        }
        return -1;
    }
}

Binary search

Analysis on the idea of binary search

1. First, determine the middle subscript of the array
   mid = (left + right) / 2
2. Then compare the number findVal to arr[mid]
3. 1 findval > arr [mid], indicating that the number you want to find is on the right of mid, so you need to find it recursively to the right
   2.2 findval < arr [mid], indicating that the number you want to find is on the left of mid, so you need to find it recursively to the left
   2.3 findVal == arr[mid] Description: return if found

When do we need to end recursion
(1) End recursion when found
(2) Recurse the entire array, and findVal is still not found. You also need to end the recursion. When left > right, you need to exit

package bilibili.search;

import java.util.*;

public class BinarySearch {
    public static void main(String[] args) {
        int[] array = {12, 23, 34, 56, 56, 56, 78, 98};
        int index = binarySearch(array, 0, array.length - 1, 56);
        System.out.println("Subscript is :" + index);
        List<Integer> resList = binarySearch2(array, 0, array.length - 1, 56);
        System.out.println("The subscript is: " + resList);
    }

    //Binary lookup requires the array to be ordered
    public static int binarySearch(int[] array, int left, int right, int findValue) {
        if (left > right) {
            return -1;
        }
        int mid = (left + right) / 2;
        int value = array[mid];
        if (findValue > value) {
            //Recursion to the right
            return binarySearch(array, mid + 1, right, findValue);
        } else if (findValue < value) {
            //Recursion to the left
            return binarySearch(array, left, mid - 1, findValue);
        } else {
            return mid;
        }
    }


    //The binary search is improved to find multiple numbers in the same array
    /*
    1. Do not return the mid index value immediately after it is found
     2. Scan to the left of the mid index value and add the subscripts of all elements satisfying 1000 to the set ArrayList
     3. Scan to the right of the mid index value and add the subscripts of all elements satisfying 1000 to the set ArrayList
      4. Return Arraylist to
     */
    public static List<Integer> binarySearch2(int[] array, int left, int right, int findValue) {
        if (left > right) {
            return new ArrayList<Integer>();
        }

        int mid = (left + right) / 2;
        int value = array[mid];
        if (findValue > value) {
            //Recursion to the right
            return binarySearch2(array, mid + 1, right, findValue);
        } else if (findValue < value) {
            //Recursion to the left
            return binarySearch2(array, left, mid - 1, findValue);
        } else {
            List<Integer> resIndexlist = new ArrayList<Integer>();
            int tmp = mid - 1;
            while (true) {
                if (tmp < 0 || array[tmp] != findValue) {
                    break;
                }
                resIndexlist.add(tmp);
                tmp--;
            }
            resIndexlist.add(mid);
            int tmp2 = mid + 1;
            while (true) {
                if (tmp > right || array[tmp2] != findValue) {
                    break;
                }
                resIndexlist.add(tmp2);
                tmp2++;
            }
            return resIndexlist;
        }
    }
}

Interpolation lookup

The interpolation search algorithm is similar to binary search, except that the interpolation search starts from the adaptive mid each time. Interpolation lookup also requires the array to be ordered.

package bilibili.search;

public class InsertSearch {
    public static void main(String[] args) {
        int[] array = {1,2,3,4,5,6,8,14,25,35};
        int index = insertSearch(array,0, array.length-1,6);
        System.out.println("The subscript is: " + index);
    }
    public static int insertSearch(int[] arr,int left,int right,int findVal){
        if(left>right||findVal<arr[0]||findVal>arr[arr.length-1]){
            //The reasons for the latter two conditions should be provided here. If the value to be found is large or small, mid will be affected
            //This affects the array assignment
            return -1;
        }
        int mid = left + (findVal-arr[left])/(arr[right]-arr[left])*(right-left);
        int tmp = arr[mid];
        if(findVal>tmp){
            return insertSearch(arr,mid+1,right,findVal);
        }else if(findVal<tmp){
            return insertSearch(arr,left,mid-1,findVal);
        }else {
            return mid;
        }
    }

}

Precautions for interpolation search:
(1) For the lookup table with large amount of data and uniform keyword distribution, interpolation search is faster

(2) in the case of uneven keyword distribution, this method is not necessarily better than half search

fibonacci search

The Fibonacci search principle is similar to the first two, only changing the position of the intermediate node (MID). The mid is no longer obtained by intermediate or interpolation, but located near the golden section point, that is, mid=low+F(k-1)-1 (f represents Fibonacci sequence), as shown in the figure below

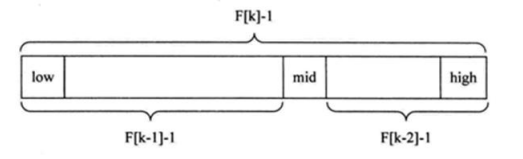
(1) From the properties of Fibonacci sequence F[k]=F[k-1]+F[k-2], we can get (F[k]-1) = (F[k-1]-1) + (F[k-2]-1) + 1. Description of the formula: as long as the length of the sequence table is F[k]-1, the table can be divided into two sections with the length of F[k-1]-1 and F[k-2]-1, as shown in the above figure. Thus, the middle position is mid=low+F(k-1)-1

(2) Similarly, each sub segment can be divided in the same way

(3) However, the length n of the sequence table is not necessarily equal to F[k]-1, so the length n of the original sequence table needs to be increased to F[k]-1. As long as the K value here can make F[k]-1 exactly greater than or equal to N, it can be obtained from the following code. After the length of the sequence table increases, the new positions (from n+1 to F[k]-1) can be assigned as the value of n position.
while(n>fib(k)-1)
k++;

package bilibili.search;
import java.util.Arrays;
public class FibSearch {
    public static void main(String[] args) {
        int[] array = {12, 23, 34, 56, 67, 78, 89};
        int index = fibSearch(array, 56);
        System.out.println("The subscript is: " + index);
    }
    //First construct a Fibonacci sequence
    public static int[] fib() {
        int maxSize = 20;
        int[] fib = new int[maxSize];
        fib[0] = 1;
        fib[1] = 1;
        for (int i = 2; i < maxSize; i++) {
            fib[i] = fib[i - 1] + fib[i - 2];
        }
        return fib;
    }
    //fibonacci search 
    public static int fibSearch(int[] array, int findVal) {
        int right = array.length - 1;
        int left = 0;
        int k = 0;//k represents the subscript of Fibonacci sequence
        int[] f = fib();
        while (array.length > f[k] - 1) {
            k++;
        }
        //At this time f[k]-1, it may be greater than the length of the array
        int[] tmp = Arrays.copyOf(array, f[k] - 1);
        for (int i = right + 1; i < f[k] - 1; i++) {
            tmp[i] = array[right];
        }
        while (left <= right) {
            int mid = f[k - 1] - 1 + left;
            if (findVal < tmp[mid]) {
                right = mid - 1;
                k = k - 1;
            } else if (findVal > tmp[mid]) {
                left = mid + 1;
                k = k - 2;
            } else {
                if (mid < right) {
                    return mid;
                } else {
                    return right;
                }

            }
        }
        return -1;
    }
}