On the right side of the page, there is a directory index, which can jump to the content you want to see according to the title
If not on the right, look for the left

Main article: https://blog.csdn.net/grd_java/article/details/120526149

Why is there a map

1. Linear table and tree, linear table is limited to a direct precursor and a direct successor, and the tree has only one direct precursor (parent node)
2. When we need many to many relationships, we need the data structure of graph

What is a graph

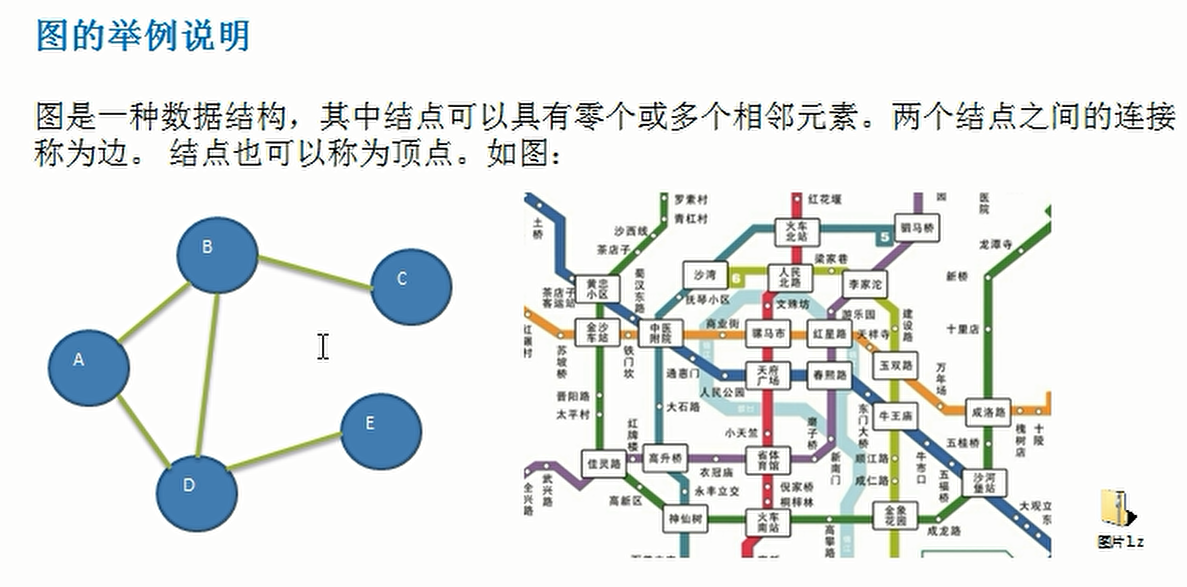
1. An edge is a connection between two nodes
2. Vertices are nodes
3. Undirected graph, the connection between vertices has no direction. A-B can be from a to B and from B to a, while a directed graph can only have one direction
4. Path, the path from one vertex to another. For example, the path of D - > C has D-B-C and D-A-B-C
   
5. Directed graph, the connection between vertices has direction
6. Weighted graph, the direct connection of vertices with weights, is also known as net

Representation of Graphs

1. Adjacency matrix (two-dimensional array representation)
   

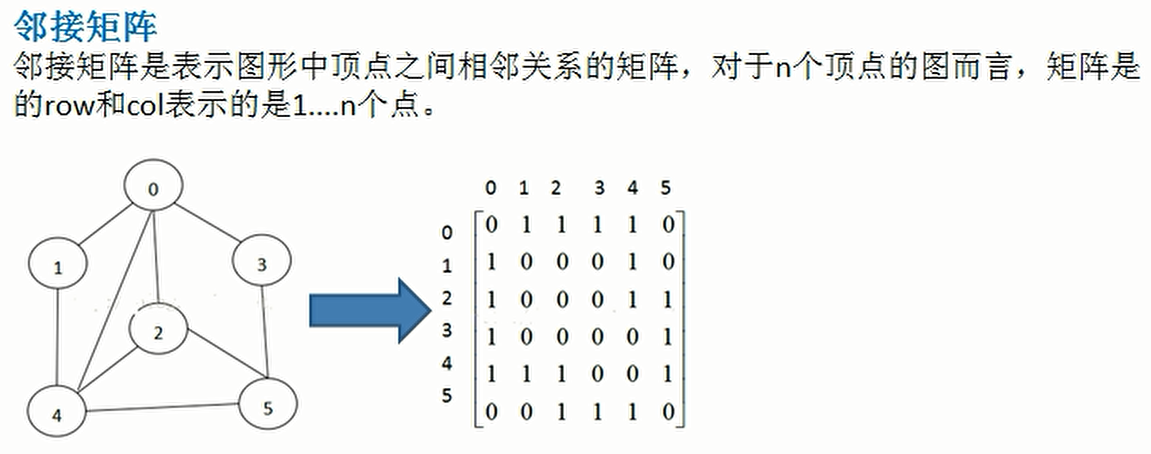
1. 1 and 0 indicate whether there is a direct connection between the two vertices. For example, arr[0][1]=1, then 0 and 1 are connected to each other

1. Adjacency list (linked list)
   

1, Code implementation

1. Create drawing

1. thinking

1. Save vertices through a List,
2. The connection relationship between vertices is represented by two-dimensional array, that is, the adjacency matrix

1. Operation effect
   
   3. Code

import java.util.ArrayList;
import java.util.Arrays;

public class Test {

    public static void main(String[] args) {
        String[] arr = {"0","1","2","3","4","5"};
        Graph graph = new Graph(arr.length);
        graph.insertVertexs(arr);
        graph.insetEdge(0,1);
        graph.insetEdge(0,4);
        graph.insetEdge(0,3);
        graph.insetEdge(0,2);
        graph.insetEdge(1,4);
        graph.insetEdge(2,4);
        graph.insetEdge(2,5);
        graph.insetEdge(3,5);
        graph.insetEdge(4,5);
        graph.showGraph();

    }

}

/**
 * Undirected graph
 */
class Graph{
    private ArrayList<String> vertexList;//Store a collection of vertices
    private int[][] edges;//Adjacency matrix for storing the connection relationship between vertices of a graph
    private int numOfEdges;//Represents the number of edges

    /**
     * Initialize construction diagram
     * @param n Number of nodes
     */
    public Graph(int n){
        edges = new int[n][n];
        vertexList = new ArrayList<>(n);
        numOfEdges = 0;
    }

    /**
     * Get the number of vertices
     */
    public int getNumOfVertex(){
        return vertexList.size();
    }

    /**
     * Get the number of edges
     */
    public int getNumOfEdges(){
        return numOfEdges;
    }

    /**
     * Get vertex based on subscript
     * @param i subscript
     */
    public String getValueByIndex(int i){
        return vertexList.get(i);
    }

    /**
     * Gets the weight of the edge that specifies two vertices
     * @param v1 First vertex
     * @param v2 Second vertex
     * @return Weight 
     */
    public int getFlag(int v1,int v2){
        return edges[v1][v2];
    }

    /**
     * Insert Knot 
     * @param vertex A node here uses a string to facilitate code writing
     */
    public void insertVertex(String vertex){
        vertexList.add(vertex);
    }

    /**
     * Insert multiple nodes at a time
     * @param vertexs Character array
     */
    public void insertVertexs(String[] vertexs){
        for (String s : vertexs){
            vertexList.add(s);
        }
    }

    /**
     * Add edges to connect the two vertices
     * @param v1 First vertex subscript
     * @param v2 Second vertex subscript
     * @param flag What is the representation? Two nodes are connected to each other, which is the weight of the edge
     */
    public void insertEdge(int v1,int v2,int flag){
        //Because it is an undirected graph, edges can be from v1 to v2 or from v2 to v1
        edges[v1][v2]=flag;//A-B can be connected
        edges[v2][v1]=flag;//B-A can be connected
        numOfEdges++;//Number of sides++
    }
    //Overload. If flag is not passed in, 1 is used by default to indicate that the two vertices are connected with each other, and the edge weight of the two vertices is 1
    public void insetEdge(int v1,int v2){
        insertEdge(v1,v2,1);
    }


    public void showGraph(){
        System.out.println("The leading matrix of the figure is:");
        for (int[] row : edges){
            System.out.println(Arrays.toString(row));
        }
    }
}

2. Graph traversal

1. The graph has two traversal modes, depth first (DFS) traversal and breadth first (BFS) traversal

1. Depth first traversal

Depth first traversal

1. Depth First Search
   

1. Depth first traversal: starting from the initial node, access the first adjacent node, and then access the next adjacent node with the accessed node. After each access to the current node, mark that this node has been accessed, and then access the first adjacent node of the current node
2. This access strategy is to give priority to mining down, not to access all adjacent nodes of a node horizontally. Obviously, depth first search is a recursive process

1. Operation results
   
2. code
   

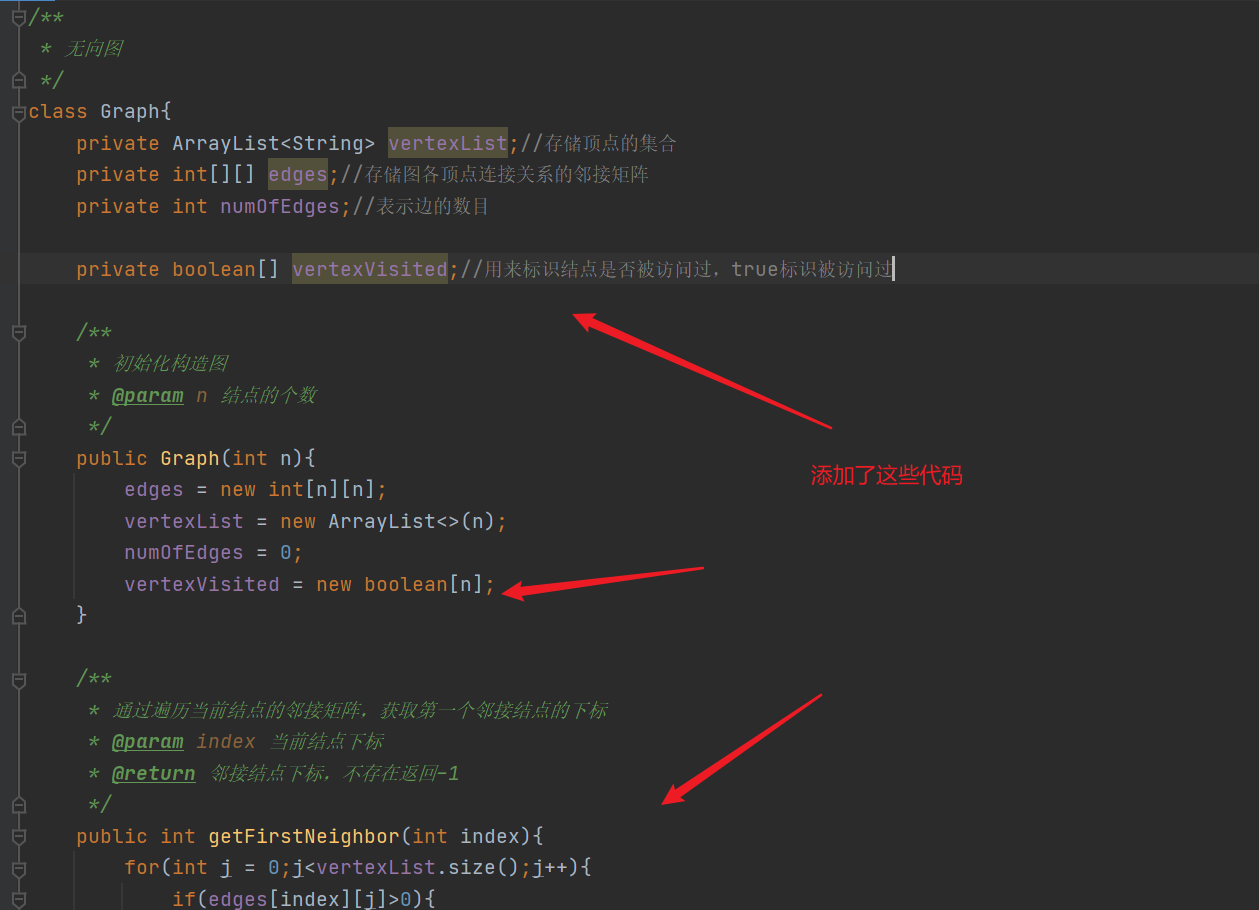
private boolean[] vertexVisited;//It is used to identify whether the node has been accessed. true indicates that it has been accessed

    /**
     * Initialize construction diagram
     * @param n Number of nodes
     */
    public Graph(int n){
        edges = new int[n][n];
        vertexList = new ArrayList<>(n);
        numOfEdges = 0;
        vertexVisited = new boolean[n];
    }

    /**
     * By traversing the adjacency matrix of the current node, the subscript of the first adjacency node is obtained
     * @param index Current node subscript
     * @return If the adjacent node subscript does not exist, return - 1
     */
    public int getFirstNeighbor(int index){
        for(int j = 0;j<vertexList.size();j++){
            if(edges[index][j]>0){
                return j;
            }
        }
        return -1;
    }

    /**
     * Find the next adjacent node according to the subscript of the first adjacent node of the current node
     * @param v1 Current node subscript
     * @param v2 Subscript of the first adjacent node of the current node
     * @return The subscript of the second adjacent node of the current node does not exist, and - 1 is returned
     */
    public int getNextNeighbor(int v1,int v2){
        for(int j = v2+1;j<vertexList.size();j++){
            if(edges[v1][j]>0){
                return j;
            }
        }
        return -1;
    }

    /**
     * Depth first traversal entry, backtracking algorithm, traversing all nodes in turn
     */
    public void dfs(){
        for (int i = 0;i<getNumOfVertex();i++){
            //If it has been accessed, skip directly
            if(!vertexVisited[i]){
                dfs(vertexVisited,i);//Not accessed, enter recursion, depth first
            }
        }
    }
    /**
     * Depth first traversal
     * @param isVisited Have you been visited
     * @param i Current node subscript
     */
    public void dfs(boolean[] isVisited,int i){
        //Output current node
        System.out.println(getValueByIndex(i));
        //Indicates that the current node has been accessed
        isVisited[i] = true;
        //Gets the subscript of the first neighbor of the current node
        int w = getFirstNeighbor(i);
        while(w != -1){//If w == -1, there are no neighbors
            //Deep recursion
            if(!isVisited[w]){//If this neighbor node has not been accessed
                dfs(isVisited,w);//Recursively traverse it
            }
            //After the deep recursion is completed, go to the next neighbor and continue the deep recursion traversal
            w = getNextNeighbor(i,w);//Get next neighbor subscript
        }
    }

2. Breadth first traversal

1. Broad first search: similar to hierarchical search, queues need to be used to ensure the order of accessing nodes, so as to access the adjacent nodes of these nodes in order
   

1. Access the initial node, mark it as accessed, and enter the queue.
2. Then out of the queue until the queue is empty and the algorithm ends
3. When a node leaves the queue, find the first adjacent node. If it does not exist, continue to leave the queue. If it exists, access the adjacent node, and then mark it as accessed and enter the queue
4. Then continue to find the next adjacent node of the inner node just out of the queue. If not, continue out of the queue

1. Operation results
   
2. Code (the array and some methods used are in the code block of depth first traversal)

	/**
     * Breadth first traversal entry, backtracking algorithm, traversing all nodes in turn
     */
    public void bfs(){
        for (int i = 0;i<getNumOfVertex();i++){
            //If it has been accessed, skip directly
            if(!vertexVisited[i]){
                bfs(vertexVisited,i);//Not accessed, enter recursion, depth first
            }
        }
        vertexVisitedInit();//The traversal is completed and the access state is initialized
    }

    /**
     * breadth-first search 
     * @param isVisited Have you been visited
     * @param i Current node subscript
     */
    public void bfs(boolean[] isVisited,int i){
        int u;//Queue header subscript
        int w;//Adjacency node
        LinkedList queue = new LinkedList<>();//queue

        System.out.print(getValueByIndex(i)+"=>");//Access the current node output first
        isVisited[i] = true;//Mark as to access
        queue.addLast(i);//Queue

        //Traverse all neighbors
        while(!queue.isEmpty()){//If the queue is not empty, it is always executed
            u = (Integer)queue.removeFirst();//Get the queue header node
            w = getFirstNeighbor(u);//Get the first neighbor of the head node
            while(w!=-1){//If the first neighbor exists
                if(!isVisited[w]){//And has not been visited
                    System.out.print(getValueByIndex(w)+"=>");//Access this node and output
                    isVisited[w] = true;//Then mark as accessed
                    queue.addLast(w);//Queue
                }
                w = getNextNeighbor(u,w);//Then traverse the breadth to get the next neighbor
            }
        }
    }

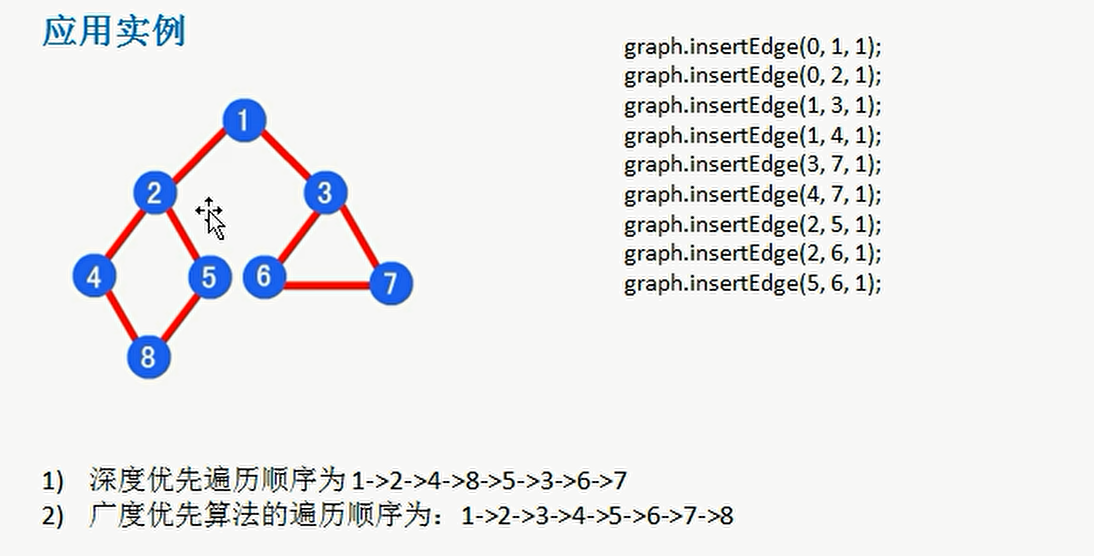
You can use this example to try the difference between depth and breadth