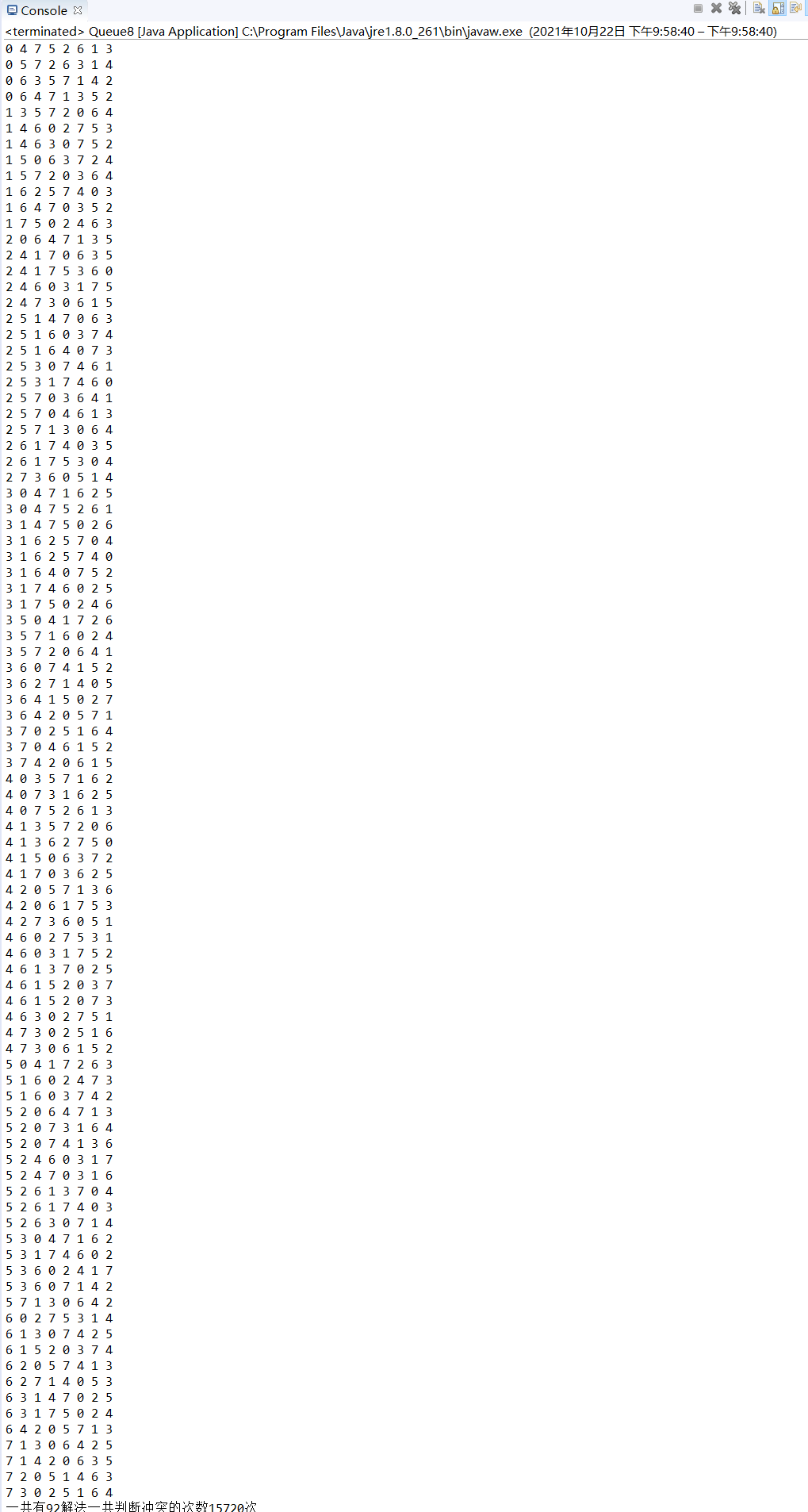catalogue
Explanation of recursive call mechanism
What kind of problems can recursion solve
What kind of problem is recursion used to solve
Analysis and implementation of maze backtracking problem (1)
Analysis and implementation of maze backtracking problem (2)
Recursive eight queens problem (backtracking algorithm)
Analysis on the algorithm of eight queens problem
Introduction and classification of sorting algorithms
Time complexity of the algorithm
2) Method of ex ante estimation
recursion
The concept of recursion
In short, recursion is a method that calls itself and passes in different variables each time. Recursion helps programmers solve complex problems and makes code concise.
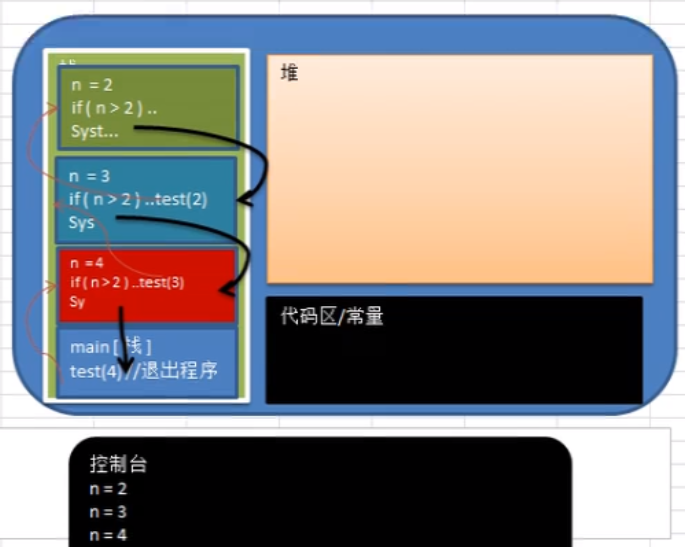
Recursive call mechanism
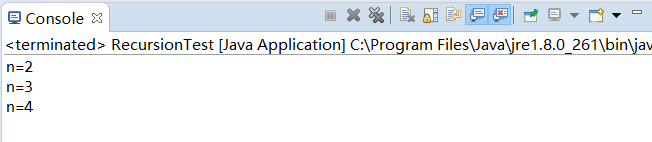
Print problem code
package recursion;
public class RecursionTest {
public static void main(String[] args) {
//Review the recursive call mechanism through the printing problem
test(4);
}
//Output what?
public static void test(int n){
if(n>2){
test(n-1);
}
System.out.println("n="+n);
}
}Operation results
Factorial problem
//Factorial
public static int factorial(int n){
if(n==1){
return 1;
}else{
return factorial(n-1)*n;
}}Operation results

Explanation of recursive call mechanism
Recursive call rule
1. When the program executes a method, it will open up an independent space (stack)
2. The data (local variables) of each space are independent.
What kind of problems can recursion solve
What kind of problem is recursion used to solve
1) Various mathematical problems: 8 queen problem, Hanoi Tower, factorial problem, maze problem, ball and basket problem (google programming competition)
2) Recursion will also be used in various algorithms, such as fast sorting, merge sorting, binary search, divide and conquer algorithm, etc
3) Problems to be solved with stack - > recursive code is relatively concise
Important rules for recursion
1) When a method is executed, a new protected independent space (stack space) is created
2) The local variables of the method are independent and will not affect each other, such as n variables
3) If a reference type variable (such as an array) is used in the method, the data of the reference type will be shared
4) Recursion must approach the condition of exiting recursion, otherwise it is infinite recursion, and StackOverflowError is dead
5) When a method is executed or returns, it will return. The result will be returned to the person who calls it. At the same time, when the method is executed or returned, the method will also be executed.
Analysis and implementation of maze backtracking problem (1)
Maze problem

code implementation
package recursion;
public class MiGong {
public static void main(String[] args) {
// First create a two-dimensional array to simulate the maze
//Map
int[][] map=new int[8][7];
//Use 1 for walls
//Set up and down to 1
for (int i = 0; i < 7; i++) {
map[0][i]=1;
map[7][i]=1;
}
//All left and right are set to 1
for (int i = 0; i < 8; i++) {
map[i][0]=1;
map[i][6]=1;
}
//Set baffle, 1 indicates
map[3][1]=1;
map[3][2]=1;
map[1][2]=1;
map[2][2]=1;
//Output map
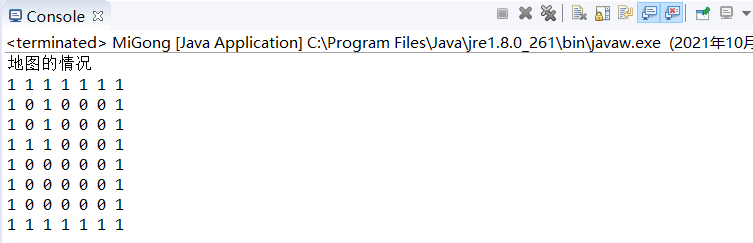
System.out.println("Map situation");
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 7; j++) {
System.out.print(map[i][j]+" ");
}
System.out.println();
}
//Use recursive backtracking to find the way for the ball
setWay( map, 1,1);
//Output a new map, the ball passes, and identifies the situation of the map
}
//Use recursive backtracking to find the way for the ball
//explain
//1.map represents a map
//2.i,j indicates where to start from on the map (1,1)
//3. If the ball can reach the map[6][5], it means that the path is found
//4. Agreement: when map[i][j] is 0, it means that the point has not passed; when map[i][j] is 1, it means that the wall, 2 means that the passage can be passed; 3 means that the point has passed, and 3 means that the point has passed, but it can not be passed
//5. When walking through the maze, you need to determine a strategy (method): down - > right - > up - > left, which means that the point can't go through, and then go back
/*
* map Represent map
* i Where do you start
* j
* If the path is found, it returns true; otherwise, it returns false
* */
public static boolean setWay(int[][] map,int i,int j) {
if (map[6][5]==2) {//The path has been found, ok
return true;
}else {
if (map[i][j]==0) {//If the current point has not passed
//According to the strategy, go down - > right - > up - > left
map[i][j]=2;//It is assumed that this point can go through
if (setWay(map, i+1, j)) {//Go down
return true;
}else if (setWay(map, i, j+1)) {//turn right
return true;
}else if (setWay(map, i-1, j)) {//Up
return true;
}else if (setWay(map, i, j-1)) {//turn left
return true;
}else {
//It means that this point is impassable and dead end
map[i][j]=3;
return false;
}
}else {
//If map [i] [J]= 0, possibly 1, 2, 3
return false;
}
}
}
}Operation results
Analysis and implementation of maze backtracking problem (2)
code implementation
package recursion;
public class MiGong {
public static void main(String[] args) {
// First create a two-dimensional array to simulate the maze
//Map
int[][] map=new int[8][7];
//Use 1 for walls
//Set up and down to 1
for (int i = 0; i < 7; i++) {
map[0][i]=1;
map[7][i]=1;
}
//All left and right are set to 1
for (int i = 0; i < 8; i++) {
map[i][0]=1;
map[i][6]=1;
}
//Set baffle, 1 indicates
map[3][1]=1;
map[3][2]=1;
// map[1][2]=1;
// map[2][2]=1;
//Output map
System.out.println("Map situation");
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 7; j++) {
System.out.print(map[i][j]+" ");
}
System.out.println();
}
//Use recursive backtracking to find the way for the ball
//setWay( map, 1,1);
setWay2(map, 1, 1);
//Output a new map, the ball passes, and identifies the situation of the map
System.out.println("The ball walked past and marked the map");
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 7; j++) {
System.out.print(map[i][j]+" ");
}
System.out.println();
}
}
//Use recursive backtracking to find the way for the ball
//explain
//1.map represents a map
//2.i,j indicates where to start from on the map (1,1)
//3. If the ball can reach the map[6][5], it means that the path is found
//4. Agreement: when map[i][j] is 0, it means that the point has not passed; when map[i][j] is 1, it means that the wall, 2 means that the passage can be passed; 3 means that the point has passed, and 3 means that the point has passed, but it can not be passed
//5. When walking through the maze, you need to determine a strategy (method): down - > right - > up - > left, which means that the point can't go through, and then go back
/*
* map Represent map
* i Where do you start
* j
* If the path is found, it returns true; otherwise, it returns false
* */
public static boolean setWay(int[][] map,int i,int j) {
if (map[6][5]==2) {//The path has been found, ok
return true;
}else {
if (map[i][j]==0) {//If the current point has not passed
//According to the strategy, go down - > right - > up - > left
map[i][j]=2;//It is assumed that this point can go through
if (setWay(map, i+1, j)) {//Go down
return true;
}else if (setWay(map, i, j+1)) {//turn right
return true;
}else if (setWay(map, i-1, j)) {//Up
return true;
}else if (setWay(map, i, j-1)) {//turn left
return true;
}else {
//It means that this point is impassable and dead end
map[i][j]=3;
return false;
}
}else {
//If map [i] [J]= 0, possibly 1, 2, 3
return false;
}
}
}
//Modify the route finding strategy to top - > right - > bottom - > left
public static boolean setWay2(int[][] map,int i,int j) {
if (map[6][5]==2) {//The path has been found, ok
return true;
}else {
if (map[i][j]==0) {//If the current point has not passed
//According to the strategy, go down - > right - > up - > left
map[i][j]=2;//It is assumed that this point can go through
if (setWay2(map, i-1, j)) {//Go up
return true;
}else if (setWay(map, i, j+1)) {//turn right
return true;
}else if (setWay(map, i-1, j)) {//down
return true;
}else if (setWay(map, i, j-1)) {//turn left
return true;
}else {
//It means that this point is impassable and dead end
map[i][j]=3;
return false;
}
}else {
//If map [i] [J]= 0, possibly 1, 2, 3
return false;
}
}
}
}
Operation effect

Recursive eight queens problem (backtracking algorithm)
The eight queens problem is an ancient and famous problem and a typical case of backtracking algorithm. The problem was proposed by international chess player Max Bethel in 1848: put eight queens on an 8 * 8 grid chess so that they can not attack each other, that is, any two Queens can not be in the same row, column or slash. Ask how many kinds of pendulum methods there are.
Using backtracking algorithm
Analysis on the algorithm of eight queens problem
1) The first queen puts the first row and the first column first
2) The second queen is placed in the first column of the second row, and then judge whether it is OK. If it is not OK, continue to put it in the second column and the third column, finish all the columns in turn, and find a suitable one.
3) Continue the third queen, or the first and second columns... Until the eighth queen can also be placed in a non conflict position, it can be regarded as finding a correct solution
4) When a correct solution is obtained, when the stack returns to the previous stack, it will start backtracking, that is, the first queen will get all the correct solutions put in the first column.
5) Then go back and continue the first queen to put the second column, and then continue to cycle through steps 1, 2, 3 and 4
Note: theoretically, a two-dimensional array should be created to represent the chessboard, but in fact, the problem can be solved by using a one-dimensional array through the algorithm. arr[8]={0,4,7,5,2,6,1,3} / / the corresponding arr subscript represents the row, that is, the queen. arr[i]=val represents the i+1 Queen, which is placed in the row i+1.
code implementation
package recursion;
public class Queue8 {
//Define a max to indicate how many queens there are
int max=8;
//Define the array array and save the results of the Queen's placement position, such as arr={0,4,7,5,2,6,1,3}
int[] array=new int[max];
static int count=0;
static int judgeCount=0;
public static void main(String[] args) {
//Test whether the 8 Queen is correct
Queue8 queue8=new Queue8();
queue8.check(0);
System.out.printf("Altogether%d solution",count);
System.out.printf("Total number of conflicts judged%d second",judgeCount);//1.5w
}
//Write a method to place the n th queen
//Special note: check means that for (int i = 0; I < max; I + +) will be entered into the check during each recursion, so there will be backtracking
private void check(int n) {
if (n==max) {//n=8, in fact, since the eight queens are ready
print();
return;
}
//Put the queen in turn and judge whether there is conflict
for (int i = 0; i < max; i++) {
//First, put the current queen n in the first column of the row
array[n]=i;
//Judge whether there is a conflict when placing the nth queen to column i
if (judge(n)) {//Never conflict
//Then put n+1 queens and start recursion
check(n+1);//
}
//If there is a conflict, continue to execute array[n]=i; That is, the nth queen is placed in the back of the line and moved to a position
}
}
//Check that when we place the nth queen, we will check whether the queen conflicts with the queen already placed in front
private boolean judge(int n) {
judgeCount++;
for (int i = 0; i <n; i++) {
//explain
//1.array[i]==array[n] indicates whether the nth queen is in the same column as the previous n-1 queens
//2.Math.abs(n-i)==Math.abs(array[n]-array[i]) indicates whether the nth queen and the ith queen are in the same slash
//n=1 place the second column 1 n=1 array[1]=1
//Math.abs(1-0)==1 Math.abs(array[n]-array[i])=Math.abs(1-0)=1
//3. It is not necessary to judge whether it is in the same line. n increases every time
if (array[i]==array[n]||Math.abs(n-i)==Math.abs(array[n]-array[i])) {
return false;
}
}
return true;
}
//Write a method to output the position of the queen
private void print() {
count++;
for (int i = 0; i < array.length; i++) {
System.out.print(array[i]+" ");
}
System.out.println();
}
}Operation results
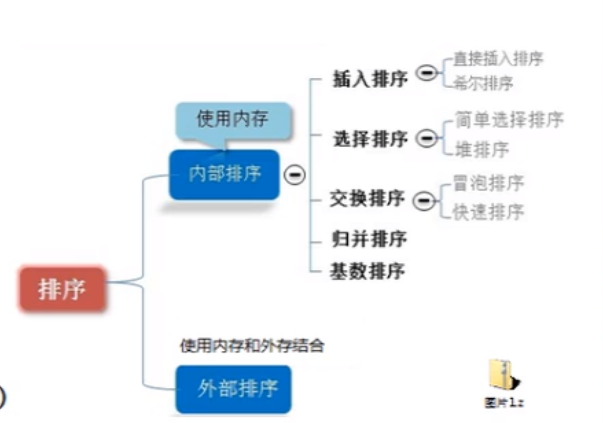
Introduction and classification of sorting algorithms
Sorting is also called sorting algorithm. Sorting is the process of sorting a group of data in a specified order.
Sorted classification
1) Internal sorting:
It refers to loading all data to be processed into internal memory for sorting
2) External sort method:
The amount of data is too large to be loaded into memory, so it needs to be sorted with the help of external storage
3) Classification of common sorting algorithms
Time complexity of the algorithm
Two methods to measure the execution time of a program (algorithm)
1) Post statistical method
This method is feasible, but there are two problems: first, to evaluate the performance of the designed algorithm, we need to actually run the program; Second, the statistics of the obtained time depend on the computer's hardware, software and other environmental factors. In this way, it is necessary to run in the same state of the same computer in order to compare the speed of that algorithm.
2) Method of ex ante estimation
The time complexity of an algorithm is analyzed to determine which algorithm changes
Time frequency
The time spent by an algorithm is in direct proportion to the execution times of the statements in the algorithm. Whichever algorithm has more execution times of the statements, it takes more time. The execution times of the statements in an algorithm are called statement frequency or time frequency. Record as T(n)
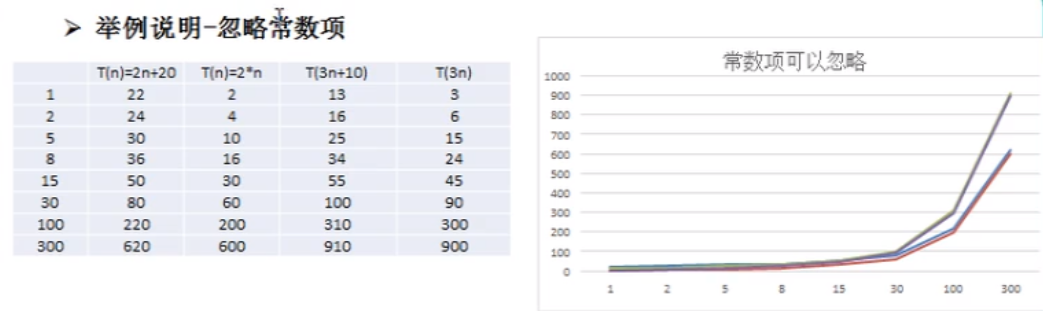
Conclusion: 1) with the increase of N, the executive curves of 2n+20 and 2n are infinitely close, and 20 can be ignored
2)3n+10 and 3n as n becomes larger, the execution curve is infinitely close, and 10 can be ignored