A Probe into the Principle of Priority BlockingQueue

_PriorityBlockingQueue is an unbounded blocking queue with priority. Each time a queue comes out, it returns the element with the highest or lowest priority. Internally, it is implemented using a balanced binary tree heap, so traversing the queue elements directly is not guaranteed to be ordered.Mouth.

(1). Structure

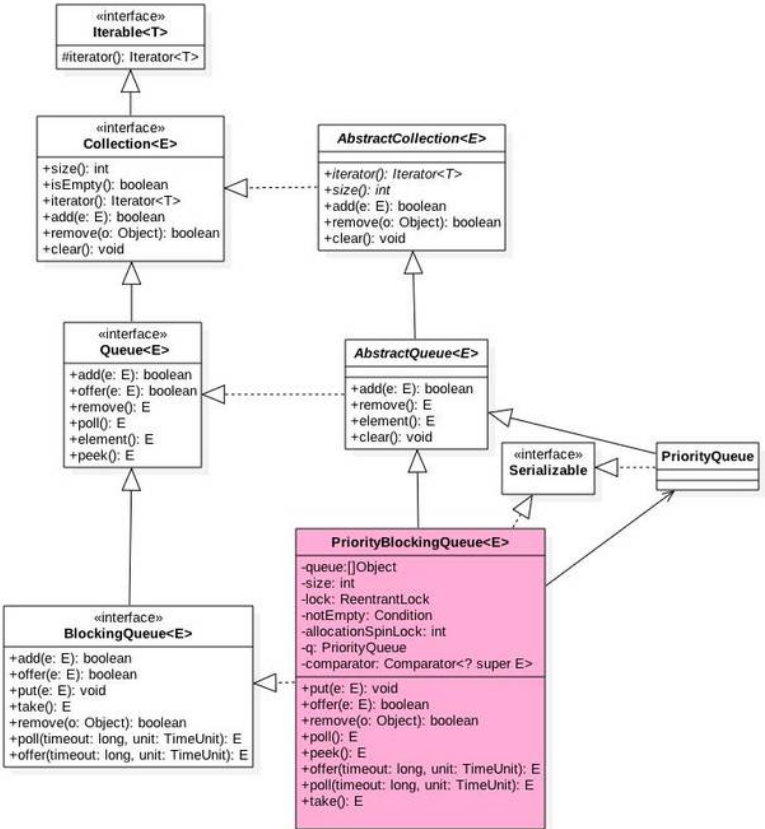
_PriorityBlockingQueue has an array queue inside it to store queue elements and size to store the number of elements. AlloionSpinLock is a spin lock that uses CAS operations to ensure that only one thread can operate on the queue with a state of 0 or 1.

_There is no notFull conditional variable because the queue is unbound and the queue entry operation is non-blocking.

(2). Principle introduction of PriorityBlockingQueue

1). offer operation

_Insert an element into the queue, because it is an unbound queue, so it must return true.

public boolean offer(E e) {
    // Make a non-empty judgment on the elements in the queue
    if (e == null)
        throw new NullPointerException();
    // Locking
    final ReentrantLock lock = this.lock;
    lock.lock();
    int n, cap;
    Object[] array;
    // Expansion if current number of elements >=queue capacity
    while ((n = size) >= (cap = (array = queue).length))
        tryGrow(array, cap);
    try {
        // Comparator, if there is an incoming comparator, use a custom comparator, if there is no default
        Comparator<? super E> cmp = comparator;
        if (cmp == null)
            // n is the first empty slot in the original queue, e is the queued element, and array is the queue
            siftUpComparable(n, e, array);
        else
            siftUpUsingComparator(n, e, array, cmp);
        // Number of queue elements + 1
        size = n + 1;
        // Unlock all conditional blockages due to an empty queue pending
        notEmpty.signal();
    } finally {
        lock.unlock();
    }
    return true;
}
// Expansion operation
private void tryGrow(Object[] array, int oldCap) {
    // Release lock
    // Only one thread can successfully expand with CAS control, releasing locks to allow other threads to queue and queue, reducing concurrency
    lock.unlock();
    Object[] newArray = null;
    // This is also a lock, allowing only one thread to expand
    if (allocationSpinLock == 0 &&
        UNSAFE.compareAndSwapInt(this, allocationSpinLockOffset, 0, 1)) {
        try {
            // If oldCap is less than 64, expansion is 2 times+2, if greater, expansion is 50%
            int newCap = oldCap + ((oldCap < 64) ? (oldCap + 2) : (oldCap >> 1));
            // Capacity expanded according to previous algorithm If overflow, minimum capacity expanded is original capacity+1
            if (newCap - MAX_ARRAY_SIZE > 0) {
                int minCap = oldCap + 1;
                // If the minimum expansion overflows or is less than 0, then expansion fails
                if (minCap < 0 || minCap > MAX_ARRAY_SIZE)
                    throw new OutOfMemoryError();
                newCap = MAX_ARRAY_SIZE; // Expand to Limit Size
            }
            // If there is no overflow under normal capacity expansion, create a new array of expanded size
            if (newCap > oldCap && queue == array)
                newArray = new Object[newCap];
        } finally {
            allocationSpinLock = 0;// Unlock
        }
    }
    // After the first thread acquires the lock, the second thread comes here directly, freeing up CPU resources to the first thread
    if (newArray == null)
        Thread.yield();
    // Lock, determine and copy arrays
    lock.lock();
    if (newArray != null && queue == array) {
        queue = newArray;
        System.arraycopy(array, 0, newArray, 0, oldCap);
    }
}
// Build Heap
private static <T> void siftUpComparable(int k, T x, Object[] array) {
    Comparable<? super T> key = (Comparable<? super T>) x;
    while (k > 0) {
        // Find the parent node of k and replace it with k if k is less than the value of the parent node
        // Until k is greater than or equal to the value of the parent node, a minimal heap is constructed (all parent nodes are less than child nodes)
        int parent = (k - 1) >>> 1;
        Object e = array[parent];
        if (key.compareTo((T) e) >= 0)
            break;
        array[k] = e;
        k = parent;
    }
    array[k] = key;
}

2). poll operation

_Gets the element of the internal root node, returns null if the queue is empty

public E poll() {
    final ReentrantLock lock = this.lock;
    lock.lock();
    try {
        return dequeue();
    } finally {
        lock.unlock();
    }
}
// Gets the element of the internal root node, returns null if the queue is empty
private E dequeue() {
    // Determine if the queue is empty
    int n = size - 1;
    if (n < 0)
        return null;
    else {
        // Remove the nth element as x
        // Remove element 0 as result
        Object[] array = queue;
        E result = (E) array[0];
        E x = (E) array[n];
        array[n] = null;
        Comparator<? super E> cmp = comparator;
        if (cmp == null)
            siftDownComparable(0, x, array, n);
        else
            siftDownUsingComparator(0, x, array, n, cmp);
        size = n;
        return result;
    }
}
// k is the free position, x is the tail element, array is the heap, n is the heap size
// Make up the parent node with the younger child until the last level, and make up with the last node
private static <T> void siftDownComparable(int k, T x, Object[] array, int n) {
    if (n > 0) {
        Comparable<? super T> key = (Comparable<? super T>)x;
        int half = n >>> 1;// unsigned right shift
        while (k < half) {
            // Child node defaults to left child
            int child = (k << 1) + 1;
            Object c = array[child];
            // Right Child
            int right = child + 1;
            // If the right child is in the heap & the left child is larger than the right child, then the right child replaces the left child as the child node, and c is the value of the child
            if (right < n && ((Comparable<? super T>) c).compareTo((T) array[right]) > 0)
                c = array[child = right];
            // Exit when tail element is smaller than child
            if (key.compareTo((T) c) <= 0)
                break;
            // Replace idle parent node with child node up
            array[k] = c;
            k = child;
        }
        array[k] = key;
    }
}

3). take operation

_Get the root node element if the queue is empty and blocked

public E take() throws InterruptedException {
    final ReentrantLock lock = this.lock;
    lock.lockInterruptibly();
    E result;
    try {
        // Loop to get root node element, suspend if queue is empty
        // Loop prevents multiple threads from being suspended at the same time
        while ( (result = dequeue()) == null)
            notEmpty.await();
    } finally {
        lock.unlock();
    }
    return result;
}

(3). Summary

Internally, the binary tree heap is used to maintain element priority, and an expandable array is used as the data structure for element storage. When queuing, ensure that the queued element is the root node, and reset the entire heap to a very small heap.

_An exclusive lock is used internally to control concurrency. Only one conditional variable notEmpty is used instead of notFull because the queue is unbounded and there is no full queue.