Concurrent SkipListMap is actually a concurrent version of TreeMap. TreeMap uses red and black trees and is sorted in the order of key s (natural order, custom order), but it is non-thread-safe. In concurrent environments, it is recommended to use Concurrent HashMap or ConcurrentSkipListMap.

Concurrent SkipListSet is actually a concurrent version of TreeSet. TreeSet uses a red-black tree at the bottom and is sorted in the order of key s (natural order, custom order), but it is non-thread-safe if it is Concurrent SkipListSet in a concurrent environment.

The bottom layer of Concurrent SkipListMap and Concurrent SkipListSet is implemented by using jump table data structure. The jump table is called jump table. It is a randomized data structure and can be regarded as a variant of binary tree. By using "jump" lookup, the complexity of inserting and reading data becomes O (logn). . It has the same performance as red-black tree and AVL tree, but the principle of jump table is very simple, and it is used in Redis and LeveIDB at present.

Jump table is a typical "space for time" algorithm, which improves the efficiency of search by adding forward pointers to each node. The basis of implementing jump table is to ensure the orderliness of elements.

Structural drawing

As can be seen from the figure, the jump table is mainly composed of the following parts:

• head: The node pointer responsible for maintaining the jump table.
• Jump table nodes: Keep element values, as well as multiple layers.
• Layer: Keep pointers to other elements. The number of elements crossed by high-level pointers is greater than or equal to that of low-level pointers. In order to improve the efficiency of searching, the program always starts from high-level, and then slowly reduces the level as the range of element values shrinks.
• End of the table: All of them are made up of NULL, which indicates the end of the jump table.

Source Code Analysis of Concurrent SkipListMap

Concurrent SkipListMap Class Diagram

Search node

Let's look at the process of finding 9: head(4)->4(4)->4(3)->4(2)->7(2)->7(1)->9

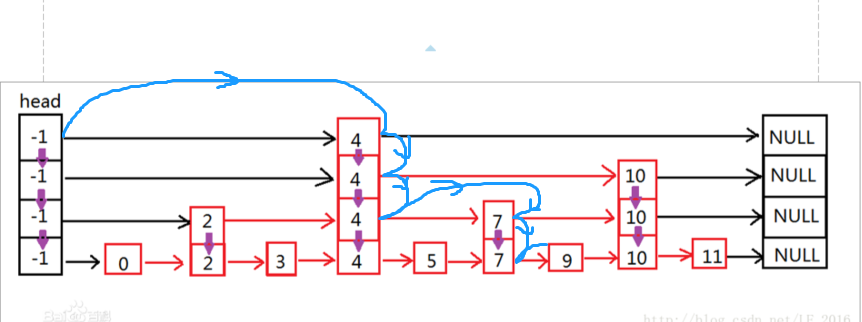
ConcurrentSkipListMap.findPredecessor()

Find the nearest point to the key, if no header node is found

    // Find the nearest point to the key, if no header node is found
    private Node<K,V> findPredecessor(Object key, Comparator<? super K> cmp) {
        if (key == null)
            throw new NullPointerException(); // don't postpone errors
        for (;;) {
            // From the beginning, q is the node to look for, r is the right node of the same level of q, d is the next level of Q.
            for (Index<K,V> q = head, r = q.right, d;;) {
                if (r != null) {
                    // n is the data node of r
                    Node<K,V> n = r.node;
                    K k = n.key;
                    if (n.value == null) {
                        if (!q.unlink(r))
                            break;           // restart
                        r = q.right;         // reread r
                        continue;
                    }
                    // Comparing the size of key, q refers to the right node of q when key > K. Continue the next cycle.
                    if (cpr(cmp, key, k) > 0) {
                        q = r;
                        r = r.right;
                        continue;
                    }
                }
                // That means we're at the bottom.
                if ((d = q.down) == null)
                    return q.node;
                // If r== null | key <= k, q points to the node at the next level of q
                q = d;
                r = d.right;
            }
        }
    }

ConcurrentSkipListMap.get()

private V doGet(Object key) {
        if (key == null)
            throw new NullPointerException();
        Comparator<? super K> cmp = comparator;
        outer: for (;;) {
            for (Node<K,V> b = findPredecessor(key, cmp), n = b.next;;) {
                Object v; int c;
                if (n == null)
                    break outer;
                Node<K,V> f = n.next;
                if (n != b.next)                // inconsistent read
                    break;
                if ((v = n.value) == null) {    // n is deleted
                    n.helpDelete(b, f);
                    break;
                }
                if (b.value == null || v == n)  // b is deleted
                    break;
                if ((c = cpr(cmp, key, n.key)) == 0) {
                    @SuppressWarnings("unchecked") V vv = (V)v;
                    return vv;
                }
                if (c < 0)
                    break outer;
                b = n;
                n = f;
            }
        }
        return null;
    }

Insert Knot

After understanding the principle of search, insertion and deletion will be easy to understand. In order to preserve the orderliness of the jump table, there are three steps: find the appropriate location - insert / delete - update the pointer of the jump table, and maintain the hierarchy.

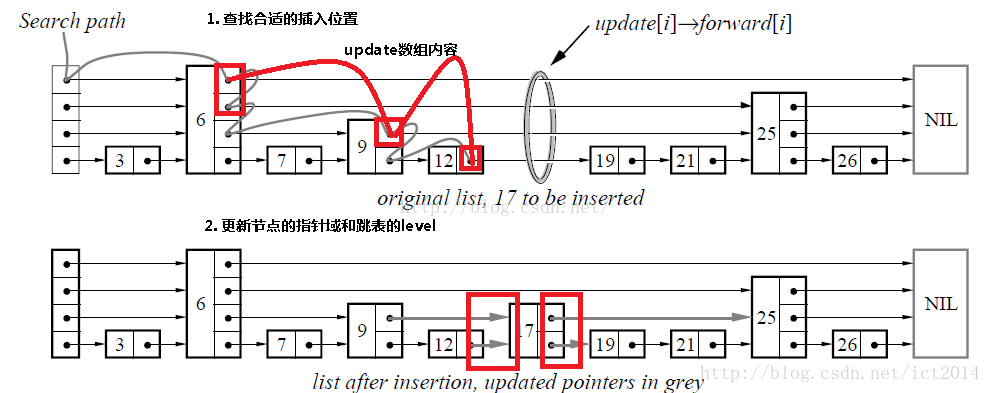
ConcurrentSkipListMap.doPut()

    private V doPut(K key, V value, boolean onlyIfAbsent) {
        Node<K,V> z;             // added node
        if (key == null)
            throw new NullPointerException();
        Comparator<? super K> cmp = comparator;
        outer: for (;;) {
            for (Node<K,V> b = findPredecessor(key, cmp), n = b.next;;) {
                if (n != null) {
                    Object v; int c;
                    Node<K,V> f = n.next;
                    if (n != b.next)               // inconsistent read
                        break;
                    if ((v = n.value) == null) {   // n is deleted
                        n.helpDelete(b, f);
                        break;
                    }
                    if (b.value == null || v == n) // b is deleted
                        break;
                    if ((c = cpr(cmp, key, n.key)) > 0) {
                        b = n;
                        n = f;
                        continue;
                    }
                    if (c == 0) {
                        if (onlyIfAbsent || n.casValue(v, value)) {
                            @SuppressWarnings("unchecked") V vv = (V)v;
                            return vv;
                        }
                        break; // restart if lost race to replace value
                    }
                    // else c < 0; fall through
                }

                z = new Node<K,V>(key, value, n);
                if (!b.casNext(n, z))
                    break;         // restart if lost race to append to b
                break outer;
            }
        }

Delete Vertex

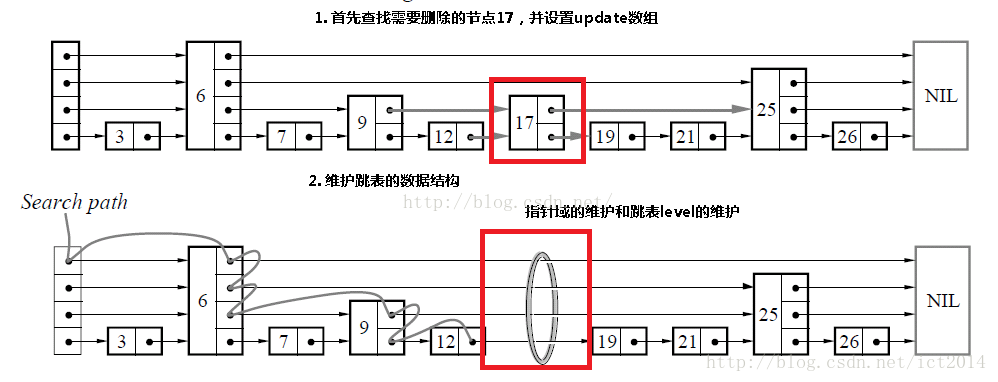
Reference resources: https://www.cnblogs.com/ygj0930/p/6543901.html