For example: int []arr= {25,69,80,57,13,};

Basic idea of bubble sorting (from small to large): compare a[0] with a[1]. If the former is greater than the latter, exchange it before and after, otherwise no operation will be done. After this step, the larger value will be in the latter, that is, a[1]. Now we need to continue to compare to the back, and the last maximum value will be placed in the last, that is, a[4]; Then find the next largest value from the previous data and put it in the penultimate position...

First round:

Because a [0] < a [1], there will be no change in the first comparison: 25, 69, 80, 57, 13

Because a [1] < a [2], there will be no change in the second comparison: 25, 69, 80, 57, 13

Because a [2] > a [3], the third comparison needs to exchange positions:     25，69，57，80，13

Because a [3] > a [4], the fourth comparison needs to exchange positions:     25，69，57，13，80

In the first round of comparison, the contents of this array will become: 25, 69, 57, 13, 80

In the second round of comparison, the contents of this array will change to: 25, 57, 13, 69, 80

In the third round of comparison, the contents of this array will become: 25, 13, 57, 69, 80

In the fourth round of comparison, the contents of this array will become: 13, 25, 57, 69, 80

The code implements the following:

	int []arr= {25,69,80,57,13};
		int tmp;
		for(int i=0;i<4;i++) {
			if(arr[i]>arr[i+1]) {
				tmp=arr[i];
				arr[i]=arr[i+1];
				arr[i+1]=tmp;
			}
		}
		for(int i=0;i<arr.length;i++) {
		System.out.print(arr[i]+" ");
		}

Arr.length retrieves the length / size of the array, where arr.length=5;

If is compared, and if it is satisfied, it is exchanged.

This only completes the first round of exchange and finds the maximum value:

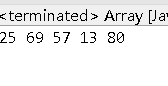
Round 2: do the for loop again as above

int []arr= {25,69,80,57,13};
		int tmp;
		for(int i=0;i<4;i++) {
			if(arr[i]>arr[i+1]) {
				tmp=arr[i];
				arr[i]=arr[i+1];
				arr[i+1]=tmp;
			}
		}
		System.out.print("first round:");
		for(int i=0;i<arr.length;i++) {
		System.out.print(arr[i]+" ");
		}
		System.out.println();
		for(int i=0;i<3;i++) {
			if(arr[i]>arr[i+1]) {
				tmp=arr[i];
				arr[i]=arr[i+1];
				arr[i+1]=tmp;
			}
		}
		System.out.print("Second round:");
		for(int i=0;i<arr.length;i++) {
		System.out.print(arr[i]+" ");
		}

The operation result is:

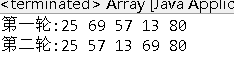
  It can be seen from this that if you continue to write two for loops, the sorting will be completed. A total of four for loops are required for four rounds of comparison. Therefore, if you carry out another for outside, there will be no need to duplicate the code. The most detailed point is the termination value in the for loop of the second layer. It can be seen from the above analysis, The value inside will change, and the changed value is just related to the value of the for loop outside. Of course, the premise is that the outer for loop is increasing. If it is decreasing, you need to find another layer of logical relationship. If you find this layer of logical relationship, you can write the bubble sorting code.

		int []arr= {25,69,80,57,13};
		int tmp;
	for(int j=0;j<4;j++) {
		for(int i=0;i<4-j;i++) {
			if(arr[i]>arr[i+1]) {
				tmp=arr[i];
				arr[i]=arr[i+1];
				arr[i+1]=tmp;
			}
			
		}
		System.out.print("The first"+(j+1)+"round:");
		for(int i=0;i<arr.length;i++) {
			System.out.print(arr[i]+" ");
			}
			System.out.println();
	}

The result is

  At this point, the operation process from simple to complex is completed, and it is simple from death to life

Look closely at the values in the code that change in different arrays

Only the number of rounds and the number of times the inner layer is compared

Slight improvement and array modification

		int []arr= {25,69,80,57,13,50,40};
		int tmp;
	for(int j=0;j<arr.length-1;j++) {//Number of rounds performed
		for(int i=0;i<arr.length-1-j;i++) {//Compare
			if(arr[i]>arr[i+1]) {//Exchange
				tmp=arr[i];
				arr[i]=arr[i+1];
				arr[i+1]=tmp;
			}
			
		}
		System.out.print("The first"+(j+1)+"round:");//Output according to the number of rounds
		for(int i=0;i<arr.length;i++) {
			System.out.print(arr[i]+" ");
			}
			System.out.println();
	}
	

results of enforcement

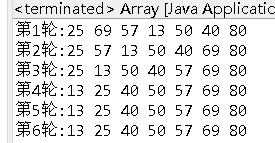
  Thus, the code is complete

The most difficult point is to write the number of cycles and the number of comparisons.

The basic idea of bubble sorting is like this. It can also be used in different programming languages. Everything is difficult at the beginning, and persistence is the most valuable