When describing DP algorithm, a classic example is the data tower problem, which is described as follows: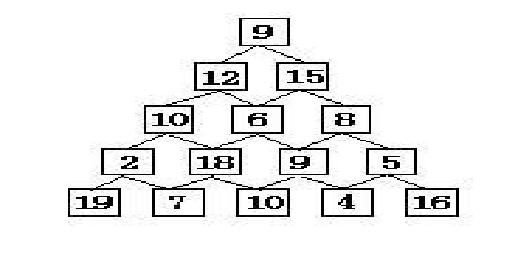

There are several towers as shown below. It is required to go from the top layer to the bottom layer. If each step can only go to the adjacent nodes, what is the maximum sum of the number of nodes passing through?

I've told you that it's a DP topic. Can you AC?
Input
The input data first includes an integer C, which represents the number of test instances. The first line of each test instance is an integer n (1 < = n < = 100), which represents the height of the data tower. Next, the number of N lines represents the data tower, where the i line has i integers, and all integers are in the range [0,99].
Output
For each test instance, the maximum sum of the possible outputs is one line per instance.
Sample Input
1
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
Sample Output
30
At the beginning of the lecture, the student listened to muddleheaded and came back to study it for himself, and found that it was OK. It's mainly to have a sense of bottom-up. There are two ways to do this: memorized search and dp. Let's start with memorized word search
The code is as follows:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int mp[101][101];
int mk[101][101];
int dp[101][101];
int d[][2]={{1,0},{1,1}};//Write the direction according to the topic.
int n;
int dfs(int x,int y)
{
	if(dp[x][y]!=-1) return dp[x][y];
	if(x==n) dp[x][y]=mp[x][y];//When you get to the bottom, you need to update dp[x][y] to mp[x][y]
	int max_=0;
	for(int i=0;i<2;i++)
	{
		int tx=x+d[i][0];
		int ty=y+d[i][1];
		//if(tx>n||ty>tx) continue;
		if(mk[tx][ty]) continue;
		mk[tx][ty]=1;
		max_=max(max_,dfs(tx,ty)+mp[x][y]);
		mk[tx][ty]=0;
	}
	return dp[x][y]=max_;
	/*else
	{
		int tx=dfs(x+1,y);
		int ty=dfs(x+1,y+1);
		dp[x][y]=max(tx,ty)+mp[x][y];
	}
	return dp[x][y];*/
}
int main()
{
	int m;
	cin>>m;
	while(m--)
	{
		cin>>n;
		for(int i=1;i<=n;i++)
		for(int j=1;j<=i;j++)
		cin>>mp[i][j];
		memset(dp,-1,sizeof(dp));//Because it might be 0, it's all - 1 at first.
		cout<<dfs(1,1)<<endl;
	}
	return 0;
}

Then there's dp thinking.. In fact, it is simpler than memory search, and it is a dynamic planning.
The code is as follows:

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int a[1010][1010];
int dp[1010][1010];
int n;
int main()
{
	cin>>n;
	for(int i=0;i<n;i++)
	{
		for(int j=0;j<=i;j++)
		cin>>a[i][j];
	}
	for(int i=0;i<n;i++)
	dp[n-1][i]=a[n-1][i];
	for(int i=n-2;i>=0;i--)
	{
		for(int j=0;j<=i;j++)
		{
			dp[i][j]=max(dp[i][j],dp[i+1][j]+a[i][j]);
			dp[i][j]=max(dp[i][j],dp[i+1][j+1]+a[i][j]);
		}
	}
	cout<<dp[0][0]<<endl;
	return 0;
}

The idea is similar to memory search. The second is personal recommendation, which is easier and more thoughtful than memory search. Hey
Work hard a, (o)/~