Today, I learned tree dp, and found that tree dp is more difficult to get started, so I decided to send a blog about tree dp.
I'm sure you all know the concept of tree dp, so we won't talk about it any more. Go straight to the example.
1, General tree DP
Title Description
A university has N employees, numbered 1-N. There is a subordinate relationship between them, that is to say, their relationship is like a tree with the principal as its root, and the parent node is the direct superior of the child node. Now there is an anniversary party. Every staff member invited to the party will increase their happiness index Ri. However, if the boss of a staff member comes to the dance, the staff member will not come to the dance in any case. So, please program and calculate, which staff can be invited to make the happiness index the largest, and find the largest happiness index.
This is a very classic tree dp. First, analyze the problem. If the boss goes, then all his subordinates can't go. If the boss doesn't go, it doesn't matter whether all his subordinates go or not, but the maximum value should be taken. Next is the state transition equation:
We set f[i][0] as the case of I not going, f[i][1] as the case of I going, then
f[i][0]+=max(f[i's company] [1],f[i's company] [0]);
f[i][1]+=f[i's company] [0];
Initialization, I f I go, then obviously f[i][1]=i's happiness index, if I don't go then f[i][1]=0;
Code at the end
1 #include<iostream> 2 #include<cstring> 3 #include<cmath> 4 #include<string> 5 #include<cstdio> 6 using namespace std; 7 struct edge 8 { 9 int num,child[6001]; 10 }g[6001]; 11 int n; 12 int a[10000]; 13 int tree[10000]; 14 int f[6001][2]; 15 int aa,bb,root; 16 void dp(int t) 17 { 18 f[t][1]=a[t];//initialization 19 f[t][0]=0;//initialization 20 for(int i=1;i<=g[t].num;i++) 21 { 22 dp(g[t].child[i]); 23 f[t][0]+=max(f[g[t].child[i]][1],f[g[t].child[i]][0]);//state transition 24 f[t][1]+=f[g[t].child[i]][0];//state transition 25 } 26 } 27 int main() 28 { 29 cin>>n; 30 for(int i=1;i<=n;i++) 31 { 32 scanf("%d",&a[i]); 33 } 34 while(scanf("%d%d",&aa,&bb)) 35 { 36 if(aa==0&&bb==0) break; 37 g[bb].num++;//Record the number of child nodes 38 g[bb].child[g[bb].num]=aa;//Save child node 39 tree[aa]=bb;//Record parent node 40 } 41 root=1; 42 while(tree[root]) root++;//Find the root 43 dp(root);//From the root dp 44 int ans=max(f[root][1],f[root][0]); 45 cout<<ans; 46 return 0; 47 }
Title Description
Bob likes playing computer games, especially strategy games. But he often can't find a way to play games quickly. Now he has a question.
He wants to build an ancient castle, and the road in the castle forms a tree. He wanted to place the least number of soldiers on the node of the tree so that they could see all the way.
Note that when a soldier is on a node, all sides connected to the node will be visible.
Please program a tree to help Bob figure out the minimum number of soldiers he needs
As like as two peas, the difference between initialization and the last question is that each person has different weights, and the weight of each question is 1.
State transition is as like as two peas; initialization, f[i][1]=1, f[i][1]=0;
Last code
1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<string> 5 #include<cstring> 6 using namespace std; 7 struct edge 8 { 9 int num,child[1501]; 10 }g[1501]; 11 int a[1501]; 12 int f[1501][2]; 13 int x,y; 14 int n; 15 void dp(int t) 16 { 17 f[t][1]=1;//Initialize to 1 18 f[t][0]=0; 19 for(int i=1;i<=g[t].num;i++) 20 { 21 dp(g[t].child[i]); 22 f[t][0]+=f[g[t].child[i]][1];//state transition 23 f[t][1]+=min(f[g[t].child[i]][1],f[g[t].child[i]][0]);//state transition 24 } 25 } 26 int main() 27 { 28 cin>>n; 29 for(int i=1;i<=n;i++) 30 { 31 scanf("%d",&x); 32 scanf("%d",&g[x].num);//Record the number of children in this node 33 for(int j=1;j<=g[x].num;j++) 34 { 35 scanf("%d",&g[x].child[j]);//Store the children of this node 36 a[j]=i;//Record father 37 } 38 } 39 int root=0; 40 while(a[root]) root++;//Find the root node 41 dp(root); 42 int ans=min(f[root][1],f[root][0]); 43 cout<<ans; 44 return 0; 45 }
Luogu P2458 [SDOI2006] security guard station
Title Description
On May 1st, in order to facilitate the evacuation and command of intensive personnel and vehicles, in order to avoid confusion and congestion in the supermarket, some security personnel are prepared to temporarily transfer from external units to maintain traffic order.
It is known that all channels of the whole underground supermarket are in the shape of a tree; some channels can be seen from each other. The general manager requires that each end point (the top of the tree) of all channels should be guarded by someone all day long. The cost of arranging security at different end points of channels is different.
Once a security guard stands at one of the endpoints of a channel, he can see not only the endpoint he is standing at, but also another endpoint of the channel. Therefore, a security guard may be able to see multiple endpoints (tree nodes) at the same time, so it is not necessary to arrange security guards at the endpoints of each channel.
Programming tasks:
Please help the supermarket manager to plan and arrange to minimize the cost under the premise of being able to guard all channel endpoints.
The difficulty is increased. If you can't understand it, you can put it first
analysis:
We find that there are only three states for all points to be finally covered:
(all of the following are for any subtree with x as the root to be covered) (we set y node as the son of y and fa as the father of x) 1.x node is covered by itself, that is, select x point to cover x point 2. The x node is covered by the son y, that is, select the Y point to cover the x point 3. The x node is covered by the father fa, that is, select the fa point to cover the x point
With these three states, we can set f[x][0/1/2] as the minimum cost when all nodes in the subtree with X as root are covered and the coverage of X point is 1 / 2 / 3
For convenience, we may set these three situations as follows:
1.f[x][0] - corresponding to 1 above
2.f[x][1] - corresponding to 2 above
3.f[x][2] - corresponding to 3 above
Since it's DP, there are always transfer equations. Let's think about how to design DP equation
Design state transfer equation:
(1) : corresponding to 1
f[x][0]=∑ min(f[y][0],f[y][1],f[y][2]) + val[x]
Where val[x] is the cost of selecting point x
It's easy for us to think that after node x is selected, we can be free (clam?), that is to say, we can ignore the state of node y of son x, because node y will be covered in any case after node x is selected, so we can take min from all States of son y and add it up
(2) : corresponding to the 3 above (3 first, because 2 is difficult to understand, put it later)
f[x][2]=∑ min(f[y][0],f[y][1])
Why is the transfer equation for case 3 written like this?
Let's understand as follows: for the x node, we want its father node fa to cover it. Then, according to our state design, at this time, we must satisfy that all points in the subtree whose root is y son of x have been covered
Then it will be transformed into a subproblem. There are only two kinds of decisions to make y subtree satisfy the conditions: either y is covered by Y's son, or Y is covered by Y itself (i.e. y node is selected). Only min accumulation is needed in these two states of Y
(3) : corresponding to 2 above
f[x][1] = ∑ min(f[y][0],f[y][1]), if all the selected are f[y][1], add min(f[y][0]-f[y][1])
At this point, we will review the dp state we designed:
Let f[x][0/1/2] be the minimum cost when all nodes in the subtree with X as root are covered and the coverage of X point is 1 / 2 / 3
First of all, if you understand the following, then the question is very simple.. If you don't understand, go back here and have a look. I'll wait for you here
For the state at this time, f[x][1] represents that for node x, let X be covered by its own son. Then, as in analysis (2), it is necessary to satisfy the condition that the subtree of Y at this time has been met before the transfer. This is the previous part: the calendar of Σ min(f[y][0],f[y][1]), so what's the next long string?
We can understand that since we want to ensure that x point is covered by our own son, then if y subtree has been covered completely at this time, but the covered state of Y is achieved through y node's own son, then x is not covered by son y, then we can generalize it. If all the decisions made by son y of X are not made through selection If we choose y point to satisfy the condition, then we must choose a child node y of X, where y satisfies the minimum of f[y][0]-f[y][1], and add the minimum difference to f[x][1], so that x point can be covered by its own son, and the state f[x][1] can be transferred reasonably
Well, if you still don't understand the design process of (3), please go back to it and read it carefully several times
If you have understood the above, Congratulations, you have lost A
Because now that we have the transfer equation, we just need the final answer
Because the topic doesn't say which is the root node of this tree, you can default 1 as the root, or open an array to record the entry of each point when adding edges, and the last point without entry is the root (but it seems that there is no difference, after all, I lost A)
The final answer is min(f[root][0],f[root][1])
1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<string> 5 #include<cstring> 6 using namespace std; 7 struct edge 8 { 9 int num,child[6001]; 10 }g[6001]; 11 int a[6001]; 12 int dp[6001][3]; 13 int root[6001]; 14 int n,aa; 15 void dfs(int x) 16 { 17 dp[x][0]=a[x]; 18 int cc=1000000000; 19 int num=0; 20 for(int i=1;i<=g[x].num;i++) 21 { 22 dfs(g[x].child[i]); 23 int t=min(dp[g[x].child[i]][0],dp[g[x].child[i]][1]); 24 dp[x][0]+=min(t,dp[g[x].child[i]][2]); 25 dp[x][1]+=t; 26 dp[x][2]+=t; 27 if(dp[g[x].child[i]][0]<dp[g[x].child[i]][1]) num++; 28 else cc=min(cc,dp[g[x].child[i]][0]-dp[g[x].child[i]][1]); 29 } 30 if(num==0) dp[x][1]+=cc; 31 } 32 int main() 33 { 34 scanf("%d",&n); 35 for(int i=1;i<=n;i++) 36 { 37 scanf("%d",&aa); 38 scanf("%d",&a[aa]); 39 scanf("%d",&g[aa].num); 40 for(int j=1;j<=g[aa].num;j++) 41 { 42 scanf("%d",&g[aa].child[j]); 43 root[g[aa].child[j]]=aa; 44 } 45 } 46 aa=1; 47 while(root[aa]) aa++; 48 dfs(aa); 49 cout<<min(dp[aa][0],dp[aa][1]); 50 return 0; 51 }
2, Tree knapsack problem (Group knapsack processing on tree)
This kind of problem is to let you choose a specified number of points on the tree to satisfy the problem of the greatest value. Generally, f[i][j] can be set to represent the optimal solution of selecting j points on this subtree.
Luogu P2015 binary apple tree
Title Description
There is an apple tree. If the branch has a fork, it must have two branches (that is, there is no node with only one son)
This tree has n nodes (leaf points or branch points), numbered 1-N, and the root number must be 1.
We describe the position of a branch by the number of nodes connected at both ends of a branch. Here is a tree with four branches
2 5
\ /
3 4
\ /
1Now there are too many branches. We need to cut them. But some branches have apples on them.
Given the number of branches that need to be kept, find out how many apples can be kept at most.
A typical tree dp problem. We set dp[i][j] as the maximum value of j points on the subtree with I as the root, because the apple tree is a binary tree, so if it is on the left subtree
Take k points, then take j-k points on the right subtree, and the state transition equation is:
dp[i][j]=max(dp[i][j],dp[i][k]+dp[v][j-k]); where V represents the child node of I.
The code is as follows:
1 #include<iostream> 2 #include<cmath> 3 #include<cstdio> 4 #include<string> 5 #include<cstring> 6 using namespace std; 7 struct edge 8 { 9 int next; 10 int to; 11 int dis; 12 }g[100000]; 13 int n,m; 14 int last[10000]; 15 int dp[1001][1001]; 16 int num; 17 int aa,bb,cc; 18 void dfs(int x,int fa) 19 { 20 for(int i=last[x];i;i=g[i].next) 21 { 22 int v=g[i].to; 23 if(v!=fa) 24 { 25 dp[v][1]=g[i].dis; 26 dfs(v,x); 27 for(int j=m;j>=1;j--) 28 for(int k=1;k<=j;k++) 29 { 30 dp[x][j]=max(dp[x][j],dp[x][k]+dp[v][j-k]);//state transition 31 } 32 } 33 } 34 } 35 void add(int from,int to,int dis) 36 { 37 g[++num].next=last[from]; 38 g[num].to=to; 39 g[num].dis=dis; 40 last[from]=num; 41 } 42 int main() 43 { 44 scanf("%d%d",&n,&m); 45 m++;//Since the topic gives the number of branches, the number of knots is equal to the number of branches plus one. 46 for(int i=1;i<n;i++) 47 { 48 scanf("%d%d%d",&aa,&bb,&cc); 49 add(aa,bb,cc); 50 add(bb,aa,cc); 51 } 52 dfs(1,1);//Search from root 53 cout<<dp[1][m]; 54 return 0; 55 }
Luogu P2014 course selection
Title Description
In order to achieve certain credits, every student in the university must choose some courses from many courses to study. In the course, some courses must be studied before some courses, such as advanced mathematics, which is always studied before other courses. Now there are N courses, each course has a credit, and each course has one or no direct prerequisite (if course a is the prerequisite of course B, then only after course a is completed can we learn course b). A student should choose M courses from these courses and ask what is the maximum credit he can get?
The general idea is the same as the previous question, but the data of this question is a forest structure. We can add a node as the whole forest
Root node, so a forest becomes a tree. For a virtual root, we only need to add 1 to the selected nodes.
Other places are exactly the same as the last question. I will not talk about it any more here, but go to the code directly:
1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<string> 5 #include<cstring> 6 using namespace std; 7 struct edge 8 { 9 int next; 10 int to; 11 }g[10000]; 12 int last[1000]; 13 int aa; 14 int n,m; 15 int num; 16 int a[1000]; 17 int dp[1000][1000]; 18 void dfs(int x,int fa) 19 { 20 dp[x][1]=a[x];//Initialize to select x Credits for this course 21 for(int i=last[x];i;i=g[i].next) 22 { 23 int v=g[i].to; 24 if(v!=fa) 25 { 26 dfs(v,x); 27 for(int j=m;j>=1;j--) 28 for(int k=1;k<=j;k++) 29 { 30 dp[x][j]=max(dp[x][j],dp[x][k]+dp[v][j-k]);//state transition 31 } 32 } 33 } 34 } 35 void add(int from,int to) 36 { 37 g[++num].next=last[from]; 38 g[num].to=to; 39 last[from]=num; 40 } 41 int main() 42 { 43 scanf("%d%d",&n,&m); 44 m++;//Because a virtual root is added, the number of nodes must be added to 1, and attention must be paid here!!! 45 for(int i=1;i<=n;i++) 46 { 47 scanf("%d%d",&aa,&a[i]);//use a Array to represent selection i Credits for this course 48 add(aa,i); 49 add(i,aa); 50 } 51 dfs(0,0);//Search from virtual heel 52 cout<<dp[0][m]; 53 return 0; 54 }
Almost the same as the previous question, you should add a virtual root node. After adding, remember to add the summary points to 1. This question is multi group data
So remember to empty as like as two peas.
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<string> 5 #include<cmath> 6 using namespace std; 7 struct edge 8 { 9 int next; 10 int to; 11 }g[1000]; 12 int last[205]; 13 int a[205]; 14 int dp[205][205]; 15 int aa; 16 int num; 17 int n,m; 18 void add(int from,int to) 19 { 20 g[++num].next=last[from]; 21 g[num].to=to; 22 last[from]=num; 23 } 24 void dfs(int x,int fa) 25 { 26 dp[x][1]=a[x]; 27 for(int i=last[x];i;i=g[i].next) 28 { 29 int v=g[i].to; 30 if(v!=fa) 31 { 32 dfs(v,x); 33 for(int j=m;j>=1;j--) 34 for(int k=1;k<=j;k++) 35 { 36 dp[x][j]=max(dp[x][j],dp[x][k]+dp[v][j-k]); 37 } 38 } 39 } 40 } 41 int main() 42 { 43 while(1) 44 { 45 scanf("%d%d",&n,&m); 46 if(n==0&&m==0) return 0; 47 m++;//One more here. 48 num=0; 49 memset(a,0,sizeof(a));//Remember to empty the array!!! 50 memset(dp,0,sizeof(dp)); 51 memset(last,0,sizeof(last)); 52 memset(g,0,sizeof(g)); 53 for(int i=1;i<=n;i++) 54 { 55 scanf("%d%d",&aa,&a[i]); 56 add(aa,i); 57 add(i,aa); 58 } 59 dfs(0,0); 60 printf("%d\n",dp[0][m]); 61 } 62 }
Killing all bug s is always easier than grabbing their brains. Make a map for you. All rooms are marked with the number of internal insects and the possibility of including the brain. The structure of the cave is like a tree, with a unique path to each room from the entrance. In order to finish the battle as soon as possible, you don't want to wait for the troops to clean up the room before moving to the next room, but you have to leave some soldiers in each room to fight against all the insects inside. The soldiers never reentered the rooms they had visited before.
Starship soldiers can fight 20 bugs. Since you don't have enough soldiers, you can only occupy some rooms and let the nerve gas do the rest of the work. At the same time, you should maximize the possibility of capturing the brain. To simplify the problem, just maximize the sum of all possible rooms containing the brain. Making such a plan is a difficult task. You need the help of a computer.
The last test case is followed by two - 1.
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<string> 5 #include<cmath> 6 using namespace std; 7 struct edge 8 { 9 int next; 10 int to; 11 }g[1000]; 12 int last[205]; 13 int a[205]; 14 int b[205]; 15 int dp[205][205]; 16 int aa,bb; 17 int num; 18 int n,m; 19 void add(int from,int to) 20 { 21 g[++num].next=last[from]; 22 g[num].to=to; 23 last[from]=num; 24 } 25 void dfs(int x,int fa) 26 { 27 for(int i=a[x];i<=m;i++)//The initialization here is different from the above topic because it has a little power. 28 dp[x][i]=b[x];//When we have a[x]When there are so many players,We can get at least b[x]Brain 29 for(int i=last[x];i;i=g[i].next) 30 { 31 int v=g[i].to; 32 if(v!=fa) 33 { 34 dfs(v,x); 35 for(int j=m;j>=a[x];j--)//We should pay attention to the boundary conditions here 36 for(int k=a[x];k<j;k++) 37 { 38 dp[x][j]=max(dp[x][j],dp[x][k]+dp[v][j-k]);//The same equation of state transition 39 } 40 } 41 } 42 } 43 int main() 44 { 45 while(1) 46 { 47 scanf("%d%d",&n,&m); 48 if(n==-1&&m==-1) return 0; 49 num=0; 50 memset(a,0,sizeof(a)); 51 memset(b,0,sizeof(b)); 52 memset(dp,0,sizeof(dp)); 53 memset(last,0,sizeof(last)); 54 memset(g,0,sizeof(g));//Empty array, basic operation 55 for(int i=1;i<=n;i++) 56 { 57 scanf("%d%d",&aa,&bb); 58 aa=(aa+19)/20; 59 a[i]=aa;//Read in point right 60 b[i]=bb; 61 } 62 for(int i=1;i<n;i++) 63 { 64 scanf("%d%d",&aa,&bb); 65 add(aa,bb); 66 add(bb,aa); 67 } 68 if(m==0)//It's a hole if m=0 Be sure to output 0; 69 printf("0\n"); 70 else //Otherwise, start searching 71 { 72 dfs(1,1); 73 printf("%d\n",dp[1][m]); 74 } 75 } 76 }
Title Description
A pay cable network plans to broadcast an important football match. Their broadcast network and user terminal form a tree structure. The root node of the tree is located in the scene of football match. The leaves are each user terminal, and other relay stations are the internal nodes of the tree.
The signal transmission cost from the relay station to the relay station and from the relay station to all user terminals is known. The total cost of a relay is equal to the total cost of the transmission signal.
Now that every user has prepared a fee to watch this wonderful football match, the cable TV network has the right to decide which users to provide signals instead of which users.
Write a program to find out a scheme to make the cable network as many users as possible without losing money.
I / O format
Input format:
The first line of the input file contains two integers N and M separated by spaces, where 2 ≤ N ≤ 3000, 1 ≤ m ≤ N-1, N is the total number of nodes in the whole cable TV network, and M is the number of user terminals.
The root node number of the first relay station is 1, the number of other relay stations is 2 to N-M, and the number of user terminals is N-M+1 to n.
The next N-M lines represent the data of one relay station, and the i+1 lines represent the data of the i relay station, with the format as follows:
K A1 C1 A2 C2 ... Ak Ck
K refers to the K nodes (relay station or user) under the relay station. Each node corresponds to A pair of integers A and C, A refers to the node number, and C refers to the cost of transmitting signals from the current relay station to node A. The last line in turn indicates the amount of money all users are prepared to pay to watch the game.
Output format:
The output file has only one line and contains an integer indicating the maximum number of users required by the above problem.
Example of input and output
2
Some difficult tree knapsack problems. First of all, it should be clear that the number of users required by the topic is the number of leaf nodes, not non leaf nodes, so when we search
By the way, you can record that when making a backpack, you only need to cycle the number of leaf nodes on this subtree.
We set dp[i][j] as the maximum benefit of selecting j leaf nodes on the subtree with I as the root. And the income value is equal to the point weight minus the edge weight, so we can deduce the state
Transfer equation: dp[x][j]=max(dp[x][j],dp[x][k]+dp[v][j-k]-g[i].dis); where V represents the child node of X
Then we enumerate the maximum number of leaf nodes on the tree with 1 as the root, which can be non negative.
Since the return may be negative, the array should be cleared as negative infinity.
Last code:
1 #include<iostream> 2 #include<cstdio> 3 #include<string> 4 #include<cmath> 5 #include<cstring> 6 using namespace std; 7 struct edge 8 { 9 int next; 10 int to; 11 int dis; 12 }g[10000]; 13 int last[10000]; 14 int a[10000]; 15 int dp[3001][3001]; 16 int aa,bb,cc; 17 int n,m,num; 18 void add(int from,int to,int dis) 19 { 20 g[++num].next=last[from]; 21 g[num].to=to; 22 g[num].dis=dis; 23 last[from]=num; 24 } 25 int dfs(int x,int fa) 26 { 27 if(x>=n-m+1)//If x It is a leaf node, so it is initialized to the point weight of this point 28 { 29 dp[x][1]=a[x]; 30 return 1;//Record the number of leaf nodes 31 } 32 int t,sum=0; 33 for(int i=last[x];i;i=g[i].next) 34 { 35 int v=g[i].to; 36 if(v!=fa) 37 { 38 t=dfs(v,x);//t Indicated by v The number of leaf nodes of the root tree 39 sum+=t;//sum Indicated by x The number of leaf nodes of the root tree 40 for(int j=sum;j>=1;j--) 41 for(int k=0;k<=j;k++) 42 { 43 dp[x][j]=max(dp[x][j],dp[x][k]+dp[v][j-k]-g[i].dis);//state transition 44 } 45 } 46 } 47 return sum; 48 } 49 int main() 50 { 51 scanf("%d%d",&n,&m); 52 memset(dp,~0x3f,sizeof(dp));//Clear for negative infinity 53 for(int i=1;i<=n-m;i++) 54 { 55 scanf("%d",&aa); 56 for(int j=1;j<=aa;j++) 57 { 58 scanf("%d%d",&bb,&cc);//Read in edge weight 59 add(i,bb,cc); 60 add(bb,i,cc); 61 } 62 } 63 for(int i=n-m+1;i<=n;i++) 64 { 65 scanf("%d",&a[i]);//Read in point right 66 } 67 for(int i=1;i<=n;i++) dp[i][0]=0;//It's very important here. If you choose 0 sub node, the revenue must be 0; 68 dfs(1,1); 69 for(int i=m;i>=1;i--) 70 { 71 if(dp[1][i]>=0)//If the return value is not negative, then the first i That's the maximum. 72 { 73 cout<<i; 74 return 0; 75 } 76 } 77 }
Luogu P1270 "visit" Art Museum
Title Description
After months of careful preparation, Peer Brelstet, a famous painter, is ready to start his next action. The structure of the museum, each corridor is either divided into two corridors, or led to an exhibition room. Peer knows the number of paintings in each exhibition room, and he accurately measures the time of passing through each corridor. Because of his experience, it takes him five seconds to get a picture. Your task is to make a program to calculate the maximum number of paintings he can steal before the police arrive.
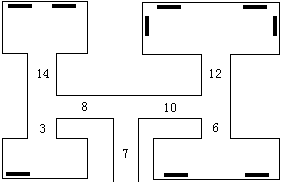
I / O format
Input format:
Line 1 is the time the police arrived, in seconds. The second line describes the structure of the art museum. It is a series of non negative integers, which appear in pairs: the first number of each pair is the time to walk through a corridor, and the second number is the number of paintings at its end; if the second number is 0, then the corridor is divided into two other corridors. The data is given in depth first order, see the example.
There are at most 20 paintings in one exhibition room. The time for passing through each corridor shall not exceed 20s. The art gallery has a maximum of 100 exhibition rooms. The police arrived within 10 minutes.
Output format:
Output the number of stolen paintings
Example of input and output
2
The reading of this question is quite poisonous. It needs to be handed back for reading. If you read the room, you can save the pictures in the room. Everything else was OK.
Let's set dp[i][j] to represent the maximum number of paintings that can be stolen by using j's time on a subtree with I as its root,
dp[i][j]=max(dp[i][j],dp[i][k]+dp[v][j-k-g[i].dis); where V is the child node of I,
g[i].dis is the distance from I to v. Because it needs to come out after stealing the painting, it needs to multiply the edge weight by 2, and it needs to run out before the police arrive, so the total time should be reduced by 1.
The code is as follows:
1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<string> 5 #include<cstring> 6 using namespace std; 7 struct edge 8 { 9 int next; 10 int to; 11 int dis; 12 }g[10000]; 13 int last[10000]; 14 int dp[2000][2000]; 15 int num,aa,bb,cc; 16 int a=1; 17 int s; 18 void add(int,int,int); 19 void dfs(int x) 20 { 21 for(int i=last[x];i;i=g[i].next) 22 { 23 int v=g[i].to; 24 dfs(v); 25 for(int j=s;j>=1;j--) 26 for(int k=0;k<=j;k++) 27 { 28 if(j-k-g[i].dis>=0) 29 dp[x][j]=max(dp[x][j],dp[x][k]+dp[v][j-k-g[i].dis]);//state transition 30 } 31 32 } 33 } 34 void read(int faa) 35 { 36 scanf("%d%d",&aa,&bb); 37 add(faa,a+1,aa*2); 38 a++; 39 if(bb==0) 40 { 41 faa=a; 42 read(faa); 43 read(faa); 44 } 45 else 46 { 47 for(int i=1;i<=bb;i++) 48 { 49 dp[a][i*5]=i; 50 } 51 } 52 } 53 void add(int from,int to,int dis) 54 { 55 g[++num].next=last[from]; 56 g[num].to=to; 57 g[num].dis=dis; 58 last[from]=num; 59 } 60 int main() 61 { 62 scanf("%d",&s); 63 s--;//Since it is necessary to come out before the police arrive, the total time is reduced by 1. 64 read(1);//Cancer reading 65 dfs(1);//Search from root 66 cout<<dp[1][s]; 67 return 0; 68 }
In fact, a God in our computer room has a unique way of thinking. He uses f[i][j] to express the time he spent stealing j pictures from a subtree with I as its root.
I have to say it's really strong.
Attach Code:
1 #include<iostream> 2 #include<cmath> 3 #include<cstdio> 4 #include<string> 5 #include<cstring> 6 using namespace std; 7 struct edge 8 { 9 int next; 10 int to; 11 int dis; 12 }g[10000]; 13 int s; 14 int aa,bb; 15 int x=1; 16 int last[10000]; 17 int dp[2001][2001]; 18 int tree[10000]; 19 int num,faa; 20 void add(int from,int to,int dis) 21 { 22 g[++num].next=last[from]; 23 g[num].to=to; 24 g[num].dis=dis; 25 last[from]=num; 26 } 27 int dfs(int y,int fa) 28 { 29 if(tree[y]==1) 30 { 31 dp[y][1]=0; 32 return 1; 33 } 34 int t,sum=0; 35 for(int i=last[y];i;i=g[i].next) 36 { 37 int v=g[i].to; 38 if(v!=fa) 39 { 40 t=dfs(v,y); 41 sum+=t; 42 for(int j=sum;j>=1;j--) 43 for(int k=0;k<j;k++) 44 { 45 dp[y][j]=max(dp[y][j],dp[y][k]+dp[v][j-k]-g[i].dis); 46 } 47 } 48 } 49 return sum; 50 } 51 void read(int faa) 52 { 53 scanf("%d%d",&aa,&bb); 54 add(faa,x+1,2*aa); 55 add(x+1,faa,2*aa); 56 x++; 57 if(bb==0) 58 { 59 faa=x; 60 read(faa); 61 read(faa); 62 } 63 else 64 { 65 int fa=x; 66 for(int i=1;i<=bb;i++) 67 { 68 tree[x+1]=1; 69 add(fa,x+1,5); 70 add(x+1,fa,5); 71 x++; 72 } 73 } 74 } 75 int main() 76 { 77 scanf("%d",&s); 78 memset(dp,~0x3f,sizeof(dp)); 79 for(int i=1;i<=2000;i++) 80 dp[i][0]=0; 81 read(1); 82 int tot=dfs(1,1); 83 for(int i=tot;i>=0;i--) 84 { 85 if(dp[1][i]+s>0) 86 { 87 cout<<i; 88 return 0; 89 } 90 } 91 return 0; 92 }
Topic background
The thief is salivating over the famous paintings in the art museum and is ready to make a big profit.
Title Description
The art gallery consists of several exhibition halls and corridors. The end of every corridor is not an exhibition hall, just
It is divided into two corridors. There are several paintings in each exhibition hall, and each painting has a value. Through the corridor and stealing paintings
It takes time.
The police will arrive at the entrance in n seconds, the most value you can get without being arrested.
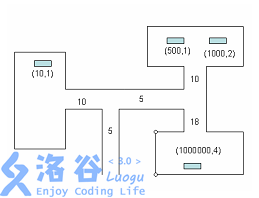
I / O format
Input format:
The first line is an integer n(n ≤ 600).
In the second line, there are several groups of integers. For each group of integers (t,x), t means it will cost t to enter the exhibition hall or pass through the corridor
In seconds, if x > 0 means there are x paintings in the exhibition hall leading to the corridor, next
x to integer (w,c) indicates that it takes C seconds to steal a painting with a value of w. if
x=0 means the corridor is divided in two. (t,c≤5; x≤30)
The input is given in depth first. No more than 300 rooms and corridors.
Output format:
Only an integer representing the maximum value that can be obtained.
Example of input and output
1500
The enhanced version of the previous question, read more cancer, but also use 01 backpack.
Read as like as two peas in each room, and then it will be exactly the same as the last 01.
The code is as follows:
1 #include<iostream> 2 #include<cstring> 3 #include<cmath> 4 #include<string> 5 #include<cstdio> 6 using namespace std; 7 struct edge 8 { 9 int next; 10 int to; 11 int dis; 12 }g[10000]; 13 int n,a=1; 14 int num; 15 int aa,bb,cc; 16 int b[10000]; 17 int dp[2001][2001]; 18 int c[10000]; 19 int last[10000]; 20 void add(int,int,int); 21 void read(int faa) 22 { 23 scanf("%d%d",&aa,&bb); 24 add(faa,a+1,aa*2); 25 a++; 26 if(bb==0) 27 { 28 faa=a; 29 read(faa); 30 read(faa); 31 } 32 else 33 { 34 for(int i=1;i<=bb;i++) 35 { 36 scanf("%d%d",&b[i],&c[i]); 37 } 38 for(int i=1;i<=bb;i++) 39 for(int j=n;j>=c[i];j--) 40 { 41 dp[a][j]=max(dp[a][j],dp[a][j-c[i]]+b[i]);//01 knapsack 42 } 43 } 44 } 45 void add(int from,int to,int dis) 46 { 47 g[++num].next=last[from]; 48 g[num].to=to; 49 g[num].dis=dis; 50 last[from]=num; 51 } 52 void dfs(int x) 53 { 54 for(int i=last[x];i;i=g[i].next) 55 { 56 int v=g[i].to; 57 dfs(v); 58 for(int j=n;j>=1;j--) 59 for(int k=0;k<=j;k++) 60 { 61 dp[x][j]=max(dp[x][j],dp[x][k]+dp[v][j-k-g[i].dis]); 62 } 63 } 64 } 65 int main() 66 { 67 scanf("%d",&n); 68 n--; 69 read(1); 70 dfs(1); 71 cout<<dp[1][n]; 72 return 0; 73 }
3, The center of gravity of trees
Definition
- The center of mass of a tree: also called the center of mass of a tree. Find a point with the largest number of subtrees and the least number of nodes. Then this point is the center of gravity of the tree. After the center of gravity is deleted, the generated trees are as balanced as possible.
Nature
-
Property 1: the sum of the distances from all points to the center of gravity in a tree is the smallest. A tree has at most two centers of gravity (for example, two points are connected to one side).
-
Property 2: add one edge to two trees to get a new tree. The center of gravity of the new tree must be the path connecting the centers of gravity of the original two trees.
-
Property 3: when a tree adds or removes a node, the center of gravity of the tree can only move one edge at most.
(the position of the center of gravity has nothing to do with the edge weight) it can't be proved, but just remember, after all, it won't be tested
Title Description
There are n villagers living in one village, and there are n-1 paths to connect the homes of these n villagers. The length of each path is 1. Now the village head wants to hold a meeting in a certain villager's home. The village head wants the sum of the distances from all the villagers to the meeting place to be the smallest. Then the village head should set the meeting place in which villager's home, and what is the minimum sum of the distances? If more than one node meets the condition, select the point with the lowest node number.
I / O format
Input format:
The first line. A number n indicates that there are n villagers.
Next n-1 lines, two numbers a and b in each line, indicate that there is a path between the home of villager A and the home of villager b.
Output format:
One line outputs two numbers x and y
x indicates in which villager's house will the village head hold the meeting
y is the minimum of the sum of distances
Example of input and output
2 4
This problem is to find the single source shortest path of the tree's center of gravity. I believe you will all know the shortest path. I will not repeat here, but the key is how to find the tree's center of gravity.
First, according to the order of dfs, a rootless tree is transformed into a rooting tree
The number of nodes of the sub book whose root is u is s[u] (including itself)
Then the largest number of subtree nodes in all subtrees of point u is
max{max{s[v]}(v is the child node of U), n-s[u] (this is because there is no "parent node" in front of the root tree, which is considered here)}
1 void dfs(int fa,int x) 2 { 3 s[x]=1; 4 for(int i=last[x];i;i=g[i].next) 5 { 6 int v=g[i].to; 7 if(v!=fa) 8 { 9 dfs(x,v); 10 s[x]+=s[v]; 11 maxx[x]=max(maxx[x],s[v]); 12 } 13 } 14 maxx[x]=max(maxx[x],n-s[x]); 15 }
Then enumerate all nodes to find the center of gravity. After that, the shortest way is to run
The code is as follows:
1 #include<iostream> 2 #include<cmath> 3 #include<cstdio> 4 #include<string> 5 #include<cstring> 6 #include<queue> 7 #define p pair<int,int> 8 #define pp make_pair 9 using namespace std; 10 priority_queue<p,vector< p >,greater< p > >q; 11 struct edge 12 { 13 int next; 14 int to; 15 int dis; 16 }g[100000]; 17 int num,aa,bb,cc,an; 18 int ans; 19 int last[100000]; 20 int s[100000]; 21 int c[100000]; 22 int d[100000]; 23 int t,dd; 24 int n,m=100000000; 25 int maxx[100000]; 26 void dfs(int fa,int x) 27 { 28 s[x]=1; 29 for(int i=last[x];i;i=g[i].next) 30 { 31 int v=g[i].to; 32 if(v!=fa) 33 { 34 dfs(x,v); 35 s[x]+=s[v]; 36 maxx[x]=max(maxx[x],s[v]); 37 } 38 } 39 maxx[x]=max(maxx[x],n-s[x]); 40 } 41 void add(int from,int to,int dis) 42 { 43 g[++num].next=last[from]; 44 g[num].to=to; 45 g[num].dis=dis; 46 last[from]=num; 47 } 48 int main() 49 { 50 cin>>n; 51 for(int i=1;i<n;i++) 52 { 53 scanf("%d%d",&aa,&bb); 54 add(aa,bb,1); 55 add(bb,aa,1); 56 } 57 dfs(1,1); 58 for(int i=1;i<=n;i++) 59 if(maxx[i]<m) 60 { 61 m=maxx[i]; 62 an=i; 63 } 64 cout<<an; 65 memset(c,0x7f,sizeof(c)); 66 c[an]=0; 67 q.push(pp(0,an)); 68 while(q.size()) 69 { 70 int t=q.top().second; 71 int dd=q.top().first; 72 q.pop(); 73 if(d[t]) continue; 74 d[t]=1; 75 for(int i=last[t];i;i=g[i].next) 76 { 77 int v=g[i].to; 78 int m=g[i].dis+dd; 79 if(c[v]>m) 80 { 81 c[v]=m; 82 q.push(pp(c[v],v)); 83 } 84 } 85 } 86 for(int i=1;i<=n;i++) 87 { 88 ans+=c[i]; 89 } 90 cout<<" "<<ans; 91 return 0; 92 }
Logue P2986 [USACO10MAR] Great Cow Gat
This problem is almost the same as the previous one, that is, there are more points of power and edge power, and some small changes need to be made.
First of all, let's find out the center of gravity of the tree, but there is a little power here. What can we do? In fact, we just need to add the point weight during initialization.
1 void dfs(int x,int fa) 2 { 3 s[x]=a[x];//Point weight initialized to current point 4 for(int i=last[x];i;i=g[i].next) 5 { 6 int v=g[i].to; 7 if(v!=fa) 8 { 9 dfs(v,x); 10 s[x]+=s[v]; 11 maxx[x]=max(maxx[x],s[v]); 12 } 13 } 14 maxx[x]=max(maxx[x],sum-s[x]);//Here we use the sum of point weights of all points as the difference 15 }
In fact, we have changed two places. Finally, the shortest path can be calculated and multiplied by the corresponding point weight.
The code is as follows:
1 #include<iostream> 2 #include<cmath> 3 #include<string> 4 #include<cstring> 5 #include<cstdio> 6 #include<queue> 7 #define p pair<long long,int> 8 #define pp make_pair 9 using namespace std; 10 priority_queue<p,vector< p >,greater< p > >q; 11 struct edge 12 { 13 int next; 14 int to; 15 int dis; 16 }g[200005]; 17 int n; 18 long long anss; 19 int ans=1000000000; 20 int an; 21 int last[100005]; 22 int s[100005]; 23 int maxx[100005]; 24 long long c[100005]; 25 int d[100005]; 26 long long a[100005]; 27 int num,t; 28 int sum; 29 long long dd; 30 int aa,bb,cc; 31 void dfs(int x,int fa) 32 { 33 s[x]=a[x];//Point weight initialized to current point 34 for(int i=last[x];i;i=g[i].next) 35 { 36 int v=g[i].to; 37 if(v!=fa) 38 { 39 dfs(v,x); 40 s[x]+=s[v]; 41 maxx[x]=max(maxx[x],s[v]); 42 } 43 } 44 maxx[x]=max(maxx[x],sum-s[x]);//Here we use the sum of point weights of all points as the difference 45 } 46 void add(int from,int to,int dis) 47 { 48 g[++num].next=last[from]; 49 g[num].to=to; 50 g[num].dis=dis; 51 last[from]=num; 52 } 53 int main() 54 { 55 scanf("%d",&n); 56 for(int i=1;i<=n;i++) 57 { 58 scanf("%lld",&a[i]); 59 sum+=a[i]; 60 } 61 for(int i=1;i<n;i++) 62 { 63 scanf("%d%d%d",&aa,&bb,&cc); 64 add(aa,bb,cc); 65 add(bb,aa,cc); 66 } 67 dfs(1,1); 68 for(int i=1;i<=n;i++) 69 { 70 if(maxx[i]<ans) 71 { 72 ans=maxx[i]; 73 an=i; 74 } 75 } 76 memset(c,0x7f,sizeof(c)); 77 c[an]=0; 78 q.push(pp(0,an)); 79 while(q.size()) 80 { 81 t=q.top().second; 82 dd=q.top().first; 83 q.pop(); 84 if(d[t]) continue; 85 d[t]=1; 86 for(int i=last[t];i;i=g[i].next) 87 { 88 int v=g[i].to; 89 long long m=g[i].dis+dd; 90 if(c[v]>m) 91 { 92 c[v]=m; 93 q.push(pp(c[v],v)); 94 } 95 } 96 } 97 for(int i=1;i<=n;i++) 98 { 99 anss+=a[i]*c[i]; 100 } 101 cout<<anss; 102 return 0; 103 }
I will write here for the introduction of tree dp. I hope this article can help you. If you have any comments or suggestions, please comment on them below. If you have any shortcomings, please correct them.