Parser is a program that converts strings into AST (Abstract Syntax Tree)

First of all, we start from the simple analysis of tree class, assuming that there is a tree node (it is a binary tree node):

class Tr:
    def __init__(self, val, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

We use this tree node to construct a tree:

t_root = Tr(5, Tr(3, Tr(4), Tr(6)),
               Tr(1, Tr(2), Tr(7)))

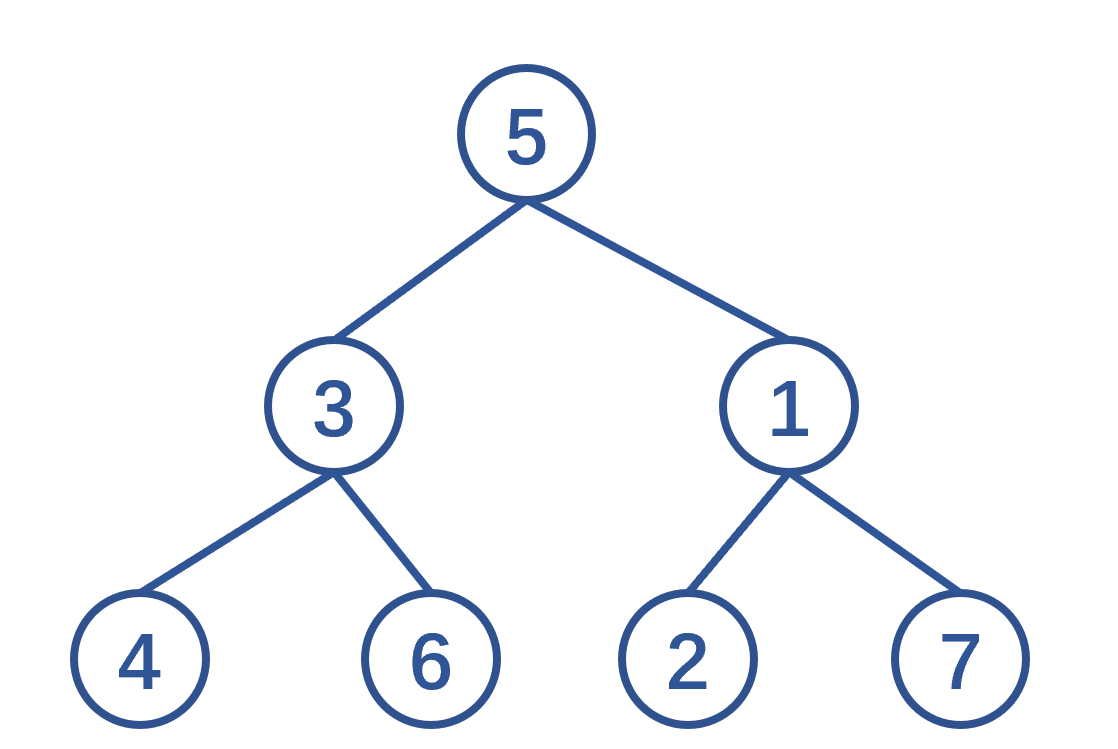
Its structure is as shown in the figure. What should we do if we want to print the path from the root node to each leaf node? Traversal tree can think of using recursion in general, but what is recursion? How to choose the parameters of recursive function? Back to what?

When thinking about recursion, we can start from the point of view of the problem and find the conditions for stopping recursion. We need to print the path from the root node to each leaf node, so the stop condition is to reach the leaf node. You can write it in code first:

def print_leaf(tr_in):
    # type: (Tr) -> None
    if tr_in.left is None and tr_in.right is None:
        # todo: stop here and do something

What do we need to do to reach the stop condition? Print required. Print what? Prints the path from the root node to the leaf node. OK, now we have reached the leaf node. The function has val of the node tr_in, but we haven't got the value of the path before. We need to have one. Let's suppose we have one. How does this come from? According to our thinking, the value of the previous path is certainly passed in by traversing nodes along the way. Then it naturally needs to be passed in as a function input:

def print_leaf(tr_in, str_in):
    # type: (Tr, str) -> None
    if tr_in.left is None and tr_in.right is None:
        print(str_in + str(tr_in.val))

Then we think about what we need to do when we don't reach the leaf node. Arriving at the leaf node is a stop flag, so not arriving at the leaf node is a recursive flag. We construct left node or right node with leaves:

def print_leaf(tr_in, str_in=""):
    # type: (Tr, str) -> None
    if tr_in.left is not None:
        print_leaf(tr_in.left, str_in + str(tr_in.val))

    if tr_in.right is not None:
        print_leaf(tr_in.right, str_in + str(tr_in.val))

    if tr_in.left is None and tr_in.right is None:
        print(str_in + str(tr_in.val))

In this way, the whole code is written. We have implemented a recursive function, which recursively calls itself when there is a child node, saves the values along the way to str_in, stops when it reaches the deepest leaf, and prints out the path. The complete code is as follows:

class Tr:

    def __init__(self, val, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right


def print_leaf(tr_in, str_in=""):
    # type: (Tr, str) -> None
    if tr_in.left is not None:
        print_leaf(tr_in.left, str_in + str(tr_in.val))

    if tr_in.right is not None:
        print_leaf(tr_in.right, str_in + str(tr_in.val))

    if tr_in.left is None and tr_in.right is None:
        print(str_in + str(tr_in.val))


if __name__ == "__main__":
    t_root = Tr(5, Tr(3, Tr(4), Tr(6)),
                   Tr(1, Tr(2), Tr(7)))
    print_leaf(t_root)

The printing effect is as follows:

534
536
512
517