this is the second article on the introduction to PyTorch. It will be continuously updated as a series of PyTorch articles.
this paper will introduce how to use PyTorch to build a simple MLP (Multi-layer Perceptron) model to realize two classification and multi classification tasks.
Data set introduction
the second classification data set is ionosphere.csv (ionosphere data set), which is UCI machine learning dataset Classical binary dataset in. It has 351 observations, 34 independent variables and 1 dependent variable (category). The category values are g(good) and b(bad). In the ionosphere.csv file, there are 351 lines. The first 34 columns are used as arguments (input X) and the last column is used as category value (output y).

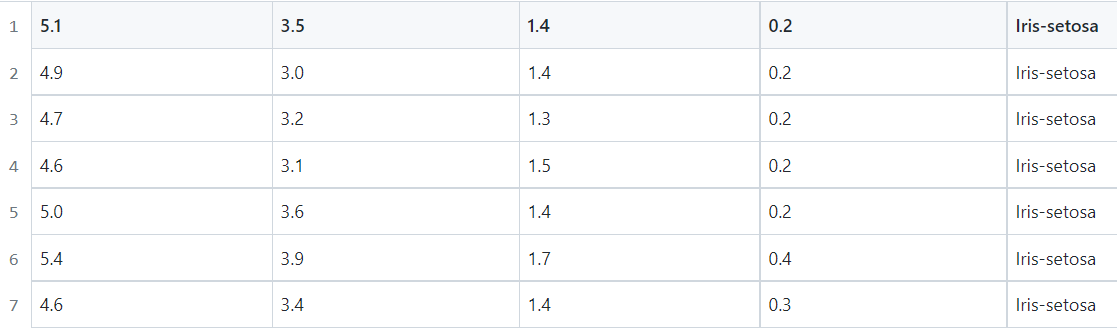
The multi classification dataset is iris.csv (iris dataset), which is UCI machine learning dataset Classical multi classification dataset in. It has a total of 150 observations, 4 independent variables (sepal length, sepal width, petal length, petal width) and 1 dependent variable (category). The category values are iris setosa, iris versicolor and iris virgin. In the iris.csv file, there are 150 lines. The first four columns are used as arguments (input X) and the last column is used as category value (output y). The first few lines of data are shown in the figure below:
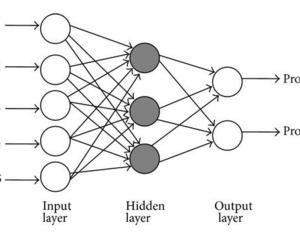
Classification model process
the basic process of using PyTorch to build a neural network model to solve the classification problem is as follows:
Among them, loading data set and dividing data set are the data processing part, building model and selecting loss function and optimizer are the part of creating model. The goal of model training is to select appropriate optimizer and training step to make the value of loss function very small. Model prediction is the prediction on model test set or new data.
Binary classification model
use PyTorch to build an MLP model to realize the secondary classification task. The model results are as follows:
The Python code for implementing the MLP model is as follows:
# -*- coding: utf-8 -*-
# pytorch mlp for binary classification
from numpy import vstack
from pandas import read_csv
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import accuracy_score
from torch import Tensor
from torch.optim import SGD
from torch.utils.data import Dataset, DataLoader, random_split
from torch.nn import Linear, ReLU, Sigmoid, Module, BCELoss
from torch.nn.init import kaiming_uniform_, xavier_uniform_
# dataset definition
class CSVDataset(Dataset):
# load the dataset
def __init__(self, path):
# load the csv file as a dataframe
df = read_csv(path, header=None)
# store the inputs and outputs
self.X = df.values[:, :-1]
self.y = df.values[:, -1]
# ensure input data is floats
self.X = self.X.astype('float32')
# label encode target and ensure the values are floats
self.y = LabelEncoder().fit_transform(self.y)
self.y = self.y.astype('float32')
self.y = self.y.reshape((len(self.y), 1))
# number of rows in the dataset
def __len__(self):
return len(self.X)
# get a row at an index
def __getitem__(self, idx):
return [self.X[idx], self.y[idx]]
# get indexes for train and test rows
def get_splits(self, n_test=0.3):
# determine sizes
test_size = round(n_test * len(self.X))
train_size = len(self.X) - test_size
# calculate the split
return random_split(self, [train_size, test_size])
# model definition
class MLP(Module):
# define model elements
def __init__(self, n_inputs):
super(MLP, self).__init__()
# input to first hidden layer
self.hidden1 = Linear(n_inputs, 10)
kaiming_uniform_(self.hidden1.weight, nonlinearity='relu')
self.act1 = ReLU()
# second hidden layer
self.hidden2 = Linear(10, 8)
kaiming_uniform_(self.hidden2.weight, nonlinearity='relu')
self.act2 = ReLU()
# third hidden layer and output
self.hidden3 = Linear(8, 1)
xavier_uniform_(self.hidden3.weight)
self.act3 = Sigmoid()
# forward propagate input
def forward(self, X):
# input to first hidden layer
X = self.hidden1(X)
X = self.act1(X)
# second hidden layer
X = self.hidden2(X)
X = self.act2(X)
# third hidden layer and output
X = self.hidden3(X)
X = self.act3(X)
return X
# prepare the dataset
def prepare_data(path):
# load the dataset
dataset = CSVDataset(path)
# calculate split
train, test = dataset.get_splits()
# prepare data loaders
train_dl = DataLoader(train, batch_size=32, shuffle=True)
test_dl = DataLoader(test, batch_size=1024, shuffle=False)
return train_dl, test_dl
# train the model
def train_model(train_dl, model):
# define the optimization
criterion = BCELoss()
optimizer = SGD(model.parameters(), lr=0.01, momentum=0.9)
# enumerate epochs
for epoch in range(100):
# enumerate mini batches
for i, (inputs, targets) in enumerate(train_dl):
# clear the gradients
optimizer.zero_grad()
# compute the model output
yhat = model(inputs)
# calculate loss
loss = criterion(yhat, targets)
# credit assignment
loss.backward()
print("epoch: {}, batch: {}, loss: {}".format(epoch, i, loss.data))
# update model weights
optimizer.step()
# evaluate the model
def evaluate_model(test_dl, model):
predictions, actuals = [], []
for i, (inputs, targets) in enumerate(test_dl):
# evaluate the model on the test set
yhat = model(inputs)
# retrieve numpy array
yhat = yhat.detach().numpy()
actual = targets.numpy()
actual = actual.reshape((len(actual), 1))
# round to class values
yhat = yhat.round()
# store
predictions.append(yhat)
actuals.append(actual)
predictions, actuals = vstack(predictions), vstack(actuals)
# calculate accuracy
acc = accuracy_score(actuals, predictions)
return acc
# make a class prediction for one row of data
def predict(row, model):
# convert row to data
row = Tensor([row])
# make prediction
yhat = model(row)
# retrieve numpy array
yhat = yhat.detach().numpy()
return yhat
# prepare the data
path = './data/ionosphere.csv'
train_dl, test_dl = prepare_data(path)
print(len(train_dl.dataset), len(test_dl.dataset))
# define the network
model = MLP(34)
print(model)
# train the model
train_model(train_dl, model)
# evaluate the model
acc = evaluate_model(test_dl, model)
print('Accuracy: %.3f' % acc)
# make a single prediction (expect class=1)
row = [1, 0, 0.99539, -0.05889, 0.85243, 0.02306, 0.83398, -0.37708, 1, 0.03760, 0.85243, -0.17755, 0.59755, -0.44945,
0.60536, -0.38223, 0.84356, -0.38542, 0.58212, -0.32192, 0.56971, -0.29674, 0.36946, -0.47357, 0.56811, -0.51171,
0.41078, -0.46168, 0.21266, -0.34090, 0.42267, -0.54487, 0.18641, -0.45300]
yhat = predict(row, model)
print('Predicted: %.3f (class=%d)' % (yhat, yhat.round()))
In the above code, CSVDataset class is the loading class of csv dataset, which is processed into the data format suitable for the model, and divided into training set and test set with a ratio of 7:3. The MLP class is an MLP model. The output layer of the model adopts Sigmoid function, the loss function adopts BCELoss, and the optimizer adopts SGD. A total of 100 times of training is performed. evaluate_ The model function is the performance of the model on the test set, and the predict function is the prediction result on the new data. The PyTorch output of MLP model is as follows:
MLP( (hidden1): Linear(in_features=34, out_features=10, bias=True) (act1): ReLU() (hidden2): Linear(in_features=10, out_features=8, bias=True) (act2): ReLU() (hidden3): Linear(in_features=8, out_features=1, bias=True) (act3): Sigmoid() )
Run the above code and the output results are as follows:
epoch: 0, batch: 0, loss: 0.7491992712020874 epoch: 0, batch: 1, loss: 0.750106692314148 epoch: 0, batch: 2, loss: 0.7033759355545044 ...... epoch: 99, batch: 5, loss: 0.020291464403271675 epoch: 99, batch: 6, loss: 0.02309396117925644 epoch: 99, batch: 7, loss: 0.0278386902064085 Accuracy: 0.924 Predicted: 0.989 (class=1)
It can be seen that the final training loss value of the MLP model is 0.02784, and the Accuracy on the test set is 0.924. The prediction on the new data is completely correct.
Multi classification model
Next, let's create an MLP model to implement the three classification tasks of iris dataset. The Python code is as follows:
# -*- coding: utf-8 -*-
# pytorch mlp for multiclass classification
from numpy import vstack
from numpy import argmax
from pandas import read_csv
from sklearn.preprocessing import LabelEncoder, LabelBinarizer
from sklearn.metrics import accuracy_score
from torch import Tensor
from torch.optim import SGD, Adam
from torch.utils.data import Dataset, DataLoader, random_split
from torch.nn import Linear, ReLU, Softmax, Module, CrossEntropyLoss
from torch.nn.init import kaiming_uniform_, xavier_uniform_
# dataset definition
class CSVDataset(Dataset):
# load the dataset
def __init__(self, path):
# load the csv file as a dataframe
df = read_csv(path, header=None)
# store the inputs and outputs
self.X = df.values[:, :-1]
self.y = df.values[:, -1]
# ensure input data is floats
self.X = self.X.astype('float32')
# label encode target and ensure the values are floats
self.y = LabelEncoder().fit_transform(self.y)
# self.y = LabelBinarizer().fit_transform(self.y)
# number of rows in the dataset
def __len__(self):
return len(self.X)
# get a row at an index
def __getitem__(self, idx):
return [self.X[idx], self.y[idx]]
# get indexes for train and test rows
def get_splits(self, n_test=0.3):
# determine sizes
test_size = round(n_test * len(self.X))
train_size = len(self.X) - test_size
# calculate the split
return random_split(self, [train_size, test_size])
# model definition
class MLP(Module):
# define model elements
def __init__(self, n_inputs):
super(MLP, self).__init__()
# input to first hidden layer
self.hidden1 = Linear(n_inputs, 5)
kaiming_uniform_(self.hidden1.weight, nonlinearity='relu')
self.act1 = ReLU()
# second hidden layer
self.hidden2 = Linear(5, 6)
kaiming_uniform_(self.hidden2.weight, nonlinearity='relu')
self.act2 = ReLU()
# third hidden layer and output
self.hidden3 = Linear(6, 3)
xavier_uniform_(self.hidden3.weight)
self.act3 = Softmax(dim=1)
# forward propagate input
def forward(self, X):
# input to first hidden layer
X = self.hidden1(X)
X = self.act1(X)
# second hidden layer
X = self.hidden2(X)
X = self.act2(X)
# output layer
X = self.hidden3(X)
X = self.act3(X)
return X
# prepare the dataset
def prepare_data(path):
# load the dataset
dataset = CSVDataset(path)
# calculate split
train, test = dataset.get_splits()
# prepare data loaders
train_dl = DataLoader(train, batch_size=1, shuffle=True)
test_dl = DataLoader(test, batch_size=1024, shuffle=False)
return train_dl, test_dl
# train the model
def train_model(train_dl, model):
# define the optimization
criterion = CrossEntropyLoss()
# optimizer = SGD(model.parameters(), lr=0.01, momentum=0.9)
optimizer = Adam(model.parameters())
# enumerate epochs
for epoch in range(100):
# enumerate mini batches
for i, (inputs, targets) in enumerate(train_dl):
targets = targets.long()
# clear the gradients
optimizer.zero_grad()
# compute the model output
yhat = model(inputs)
# calculate loss
loss = criterion(yhat, targets)
# credit assignment
loss.backward()
print("epoch: {}, batch: {}, loss: {}".format(epoch, i, loss.data))
# update model weights
optimizer.step()
# evaluate the model
def evaluate_model(test_dl, model):
predictions, actuals = [], []
for i, (inputs, targets) in enumerate(test_dl):
# evaluate the model on the test set
yhat = model(inputs)
# retrieve numpy array
yhat = yhat.detach().numpy()
actual = targets.numpy()
# convert to class labels
yhat = argmax(yhat, axis=1)
# reshape for stacking
actual = actual.reshape((len(actual), 1))
yhat = yhat.reshape((len(yhat), 1))
# store
predictions.append(yhat)
actuals.append(actual)
predictions, actuals = vstack(predictions), vstack(actuals)
# calculate accuracy
acc = accuracy_score(actuals, predictions)
return acc
# make a class prediction for one row of data
def predict(row, model):
# convert row to data
row = Tensor([row])
# make prediction
yhat = model(row)
# retrieve numpy array
yhat = yhat.detach().numpy()
return yhat
# prepare the data
path = './data/iris.csv'
train_dl, test_dl = prepare_data(path)
print(len(train_dl.dataset), len(test_dl.dataset))
# define the network
model = MLP(4)
print(model)
# train the model
train_model(train_dl, model)
# evaluate the model
acc = evaluate_model(test_dl, model)
print('Accuracy: %.3f' % acc)
# make a single prediction
row = [5.1, 3.5, 1.4, 0.2]
yhat = predict(row, model)
print('Predicted: %s (class=%d)' % (yhat, argmax(yhat)))
It can be seen that the multi category code is similar to the two category code, and is slightly different in loading data set, model structure and model training (the training batch value is 1). Run the above code and the output results are as follows:
105 45 MLP( (hidden1): Linear(in_features=4, out_features=5, bias=True) (act1): ReLU() (hidden2): Linear(in_features=5, out_features=6, bias=True) (act2): ReLU() (hidden3): Linear(in_features=6, out_features=3, bias=True) (act3): Softmax(dim=1) ) epoch: 0, batch: 0, loss: 1.4808106422424316 epoch: 0, batch: 1, loss: 1.4769641160964966 epoch: 0, batch: 2, loss: 0.654313325881958 ...... epoch: 99, batch: 102, loss: 0.5514447093009949 epoch: 99, batch: 103, loss: 0.620153546333313 epoch: 99, batch: 104, loss: 0.5514482855796814 Accuracy: 0.933 Predicted: [[9.9999809e-01 1.8837408e-06 2.4509615e-19]] (class=0)
It can be seen that the final training loss value of the MLP model is 0.5514 and the Accuracy on the test set is 0.933. The prediction on the new data is completely correct.
summary
the model code introduced in this article is open source. Github address is: https://github.com/percent4/PyTorch_Learning . In the follow-up, we will continue to introduce the content of PyTorch. Welcome to pay attention~