
1. Title
1. Title Description
Given two arrays of integers nums1 and nums2 in ascending order, and an integer
k
k
k. Define a pair of values
(
u
,
v
)
(u,v)
(u,v), where the first element is from nums1 and the second element is from nums2. Find and minimize
k
k
k pairs
(
u
1
,
v
1
)
(u1,v1)
(u1,v1),
(
u
2
,
v
2
)
(u2,v2)
(u2,v2) ...
(
u
k
,
v
k
)
(uk,vk)
(uk,vk).
_Sample input: nums1 = [1,7,11], nums2 = [2,4,6], k = 3
_Sample output: [1,2], [1,4], [1,6]
2. Infrastructure
- The basic framework code given in the C language version is as follows:
int** kSmallestPairs(int* nums1, int nums1Size, int* nums2, int nums2Size, int k, int* returnSize, int** returnColumnSizes){
}

3. Topic Link
LeetCode 373.Find and Minimum K Pair Number
Swordfinger Offer II 061.And minimum k pairs
2. Problem-solving Report
1. Idea Analysis
The structure of the_heap element stores two subscripts and a sum value, respectively. Initially, the ( 0 , 0 , s u m ) (0, 0, sum) (0,0,sum) crammed into the heap. Then one pop-up element pops up, and if duplicates are found, they need to be weighted. For pop-up elements ( i , j , s u m ) (i, j, sum) (i,j,sum), will ( i , j + 1 , s u m ) (i, j+1, sum) (i,j+1,sum), ( i , j + 2 , s u m ) (i, j+2, sum) (i,j+2,sum),...Into the heap until it encounters something smaller than the heap element. ( i + 1 , j , s u m ) (i+1, j, sum) (i+1,j,sum), ( i + 2 , j , s u m ) (i+2, j, sum) (i+2,j,sum),... Into the heap, the same thing happens. When the pop-up element reaches k k k-hour end algorithm.
2. Time Complexity
There may be at most one element in the_heap k 2 k^2 k2, so the time complexity is O ( k 2 l o g 2 k ) O(k^2log_2k) O(k2log2k) .
3. Code Details
/**********************************Small Top Heap Template******************************************/
#define lson(idx) (idx << 1|1)
#define rson(idx) ((idx + 1) << 1)
#define parent(idx) ((idx - 1) >> 1)
#define root 0
typedef struct {
int val[2];
int sum;
}DataType;
// Exchange of -1 and 1 becomes a big heap
int compareData(const DataType* a, const DataType* b) {
if(a->sum != b->sum) {
return a->sum < b->sum ? -1 : 1;
}
if (a->val[0] != b->val[0]) {
return a->val[0] < b->val[0] ? -1 : 1;
}
if (a->val[1] != b->val[1]) {
return a->val[1] < b->val[1] ? -1 : 1;
}
return 0;
}
void swap(DataType* a, DataType* b) {
DataType tmp = *a;
*a = *b;
*b = tmp;
}
typedef struct {
DataType *data;
int size;
int capacity;
}Heap;
// Internal interface, lower case hump
// The heapShiftDown interface is an internal interface, so it is distinguished by lowercase humps to adjust for sinking while deleting elements from the heap.
void heapShiftDown(Heap* heap, int curr) {
int son = lson(curr);
while(son < heap->size) {
if( rson(curr) < heap->size ) {
if( compareData( &heap->data[rson(curr)], &heap->data[son] ) < 0 ) {
son = rson(curr); // Always select nodes with smaller values
}
}
if( compareData( &heap->data[son], &heap->data[curr] ) < 0 ) {
swap(&heap->data[son], &heap->data[curr]); // If the value of the child node is less than the parent node, the exchange is performed.
curr = son;
son = lson(curr);
}else {
break; // The value of the child node is greater than that of the parent node, indicating that it is properly positioned, that the sink operation ends and that it jumps out of the cycle.
}
}
}
// The heapShiftUp interface is an internal interface, so it is distinguished by lowercase humps to adjust for the float when elements in the heap are inserted.
void heapShiftUp(Heap* heap, int curr) {
int par = parent(curr);
while(par >= root) {
if( compareData( &heap->data[curr], &heap->data[par] ) < 0 ) {
swap(&heap->data[curr], &heap->data[par]); // If the value of the child node is less than the parent node, the exchange is performed.
curr = par;
par = parent(curr);
}else {
break; // The value of the child node is larger than the parent node, indicating that it has been positioned correctly, the floating operation ends, and the cycle jumps out.
}
}
}
bool heapIsFull(Heap *heap) {
return heap->size == heap->capacity;
}
// External interface, capitalized hump
// Empty heap
bool HeapIsEmpty(Heap *heap) {
return heap->size == 0;
}
// Insertion of heap
// Insert in the last position and keep floating up
bool HeapPush(Heap* heap, DataType data) {
if( heapIsFull(heap) ) {
return false;
}
heap->data[ heap->size++ ] = data;
heapShiftUp(heap, heap->size-1);
return true;
}
// Heap Delete
// 1. When deleting the top element of a heap, place the element with the largest subscript at the bottom of the heap on the top of the pair;
// 2. Then invoke shift Down to sink this element;
// For small-top heaps, the path from root to leaf must be monotonic, so the sink operation must end at some point in the path and ensure that all heap paths remain monotonic.
bool HeapPop(Heap *heap) {
if(HeapIsEmpty(heap)) {
return false;
}
heap->data[root] = heap->data[ --heap->size ];
heapShiftDown(heap, root);
return true;
}
DataType HeapTop(Heap *heap) {
assert(!HeapIsEmpty(heap));
return heap->data[root];
}
// Create Heap
Heap* HeapCreate(DataType *data, int dataSize, int maxSize) {
int i;
Heap *h = (Heap *)malloc( sizeof(Heap) );
h->data = (DataType *)malloc( sizeof(DataType) * maxSize );
h->size = 0;
h->capacity = maxSize;
for(i = 0; i < dataSize; ++i) {
HeapPush(h, data[i]);
}
return h;
}
// Destroy heap
void HeapFree(Heap *heap) {
free(heap->data);
free(heap);
}
/**********************************Small Top Heap Template******************************************/
int** kSmallestPairs(int* nums1, int nums1Size, int* nums2, int nums2Size, int k, int* returnSize, int** returnColumnSizes){
Heap *h = HeapCreate(NULL, 0, 100000);
DataType d, tmp;
int l, r, sum;
int retSize = 0;
int first;
int **ret = (int **) malloc( sizeof(int *) * k); // (1)
*returnColumnSizes = (int *) malloc( sizeof(int) * k); // (2)
d.val[0] = 0;
d.val[1] = 0;
d.sum = nums1[0] + nums2[0];
HeapPush(h, d); // (3)
while(k-- && !HeapIsEmpty(h)) {
d = HeapTop(h); // (4)
HeapPop(h);
while(!HeapIsEmpty(h)) { // (5)
tmp = HeapTop(h);
if( compareData(&d, &tmp) == 0 ) {
HeapPop(h);
}else break;
}
ret[ retSize ] = (int *) malloc( sizeof(int) * 2 ); // (6)
ret[ retSize ][0] = nums1[ d.val[0] ];
ret[ retSize ][1] = nums2[ d.val[1] ];
(*returnColumnSizes)[retSize] = 2; // (7)
retSize++;
l = d.val[0] + 1;
r = d.val[1];
first = 1;
while(l < nums1Size && r < nums2Size) { // (8)
sum = nums1[l] + nums2[r];
if( HeapIsEmpty(h) || sum <= HeapTop(h).sum || first ) {
tmp.val[0] = l;
tmp.val[1] = r;
tmp.sum = sum;
HeapPush(h, tmp);
++r;
first = 0;
}else break;
}
l = d.val[0];
r = d.val[1] + 1;
first = 1;
while(l < nums1Size && r < nums2Size) { // (9)
sum = nums1[l] + nums2[r];
if( HeapIsEmpty(h) || sum <= HeapTop(h).sum || first ) {
tmp.val[0] = l;
tmp.val[1] = r;
tmp.sum = sum;
HeapPush(h, tmp);
++l;
first = 0;
}else break;
}
}
*returnSize = retSize;
HeapFree(h);
return ret;
}
- ( 1 ) (1) (1) Apply for a two-dimensional array;
- ( 2 ) (2) (2) Apply for a one-dimensional array;
- ( 3 ) (3) (3) Put the initial elements in the heap;
- ( 4 ) (4) (4) Pop up an element with the smallest value;
- ( 5 ) (5) (5) weight removal;
- ( 6 ) (6) (6) Fill in the list of results;
- ( 7 ) (7) (7) The length of the result list to be filled in;
- ( 8 ) (8) (8) A candidate solution is inserted;
- ( 9 ) (9) (9) A candidate solution is inserted;
3. Small knowledge of the subject
The elements of a_heap can be structured, and any structured heap operation can be accomplished by modifying the comparison function.

4. Notice for Adding Groups
_I believe most of my articles are "college students" and "elites" who can go to university, so we naturally want to "lean". If you are still a freshman, that's great. You have plenty of time. Of course, you can choose "brush opera". However, after "learning algorithms", three years you will naturally "not be in the same language".
_Then here, I have sorted out the classification of "dozens of basic algorithms" and click on Open:
_If the link is blocked or you have permission issues, you can chat with the author privately to resolve them.

_Overview of the general problem set:
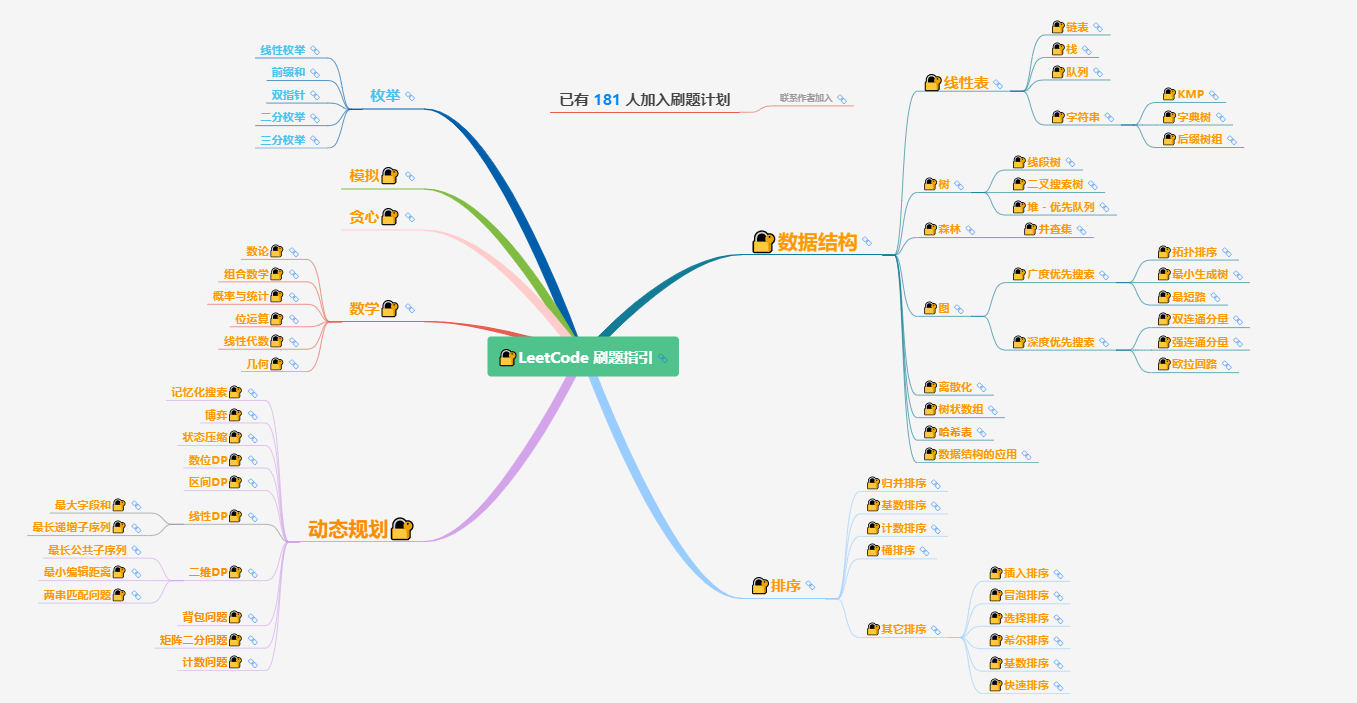
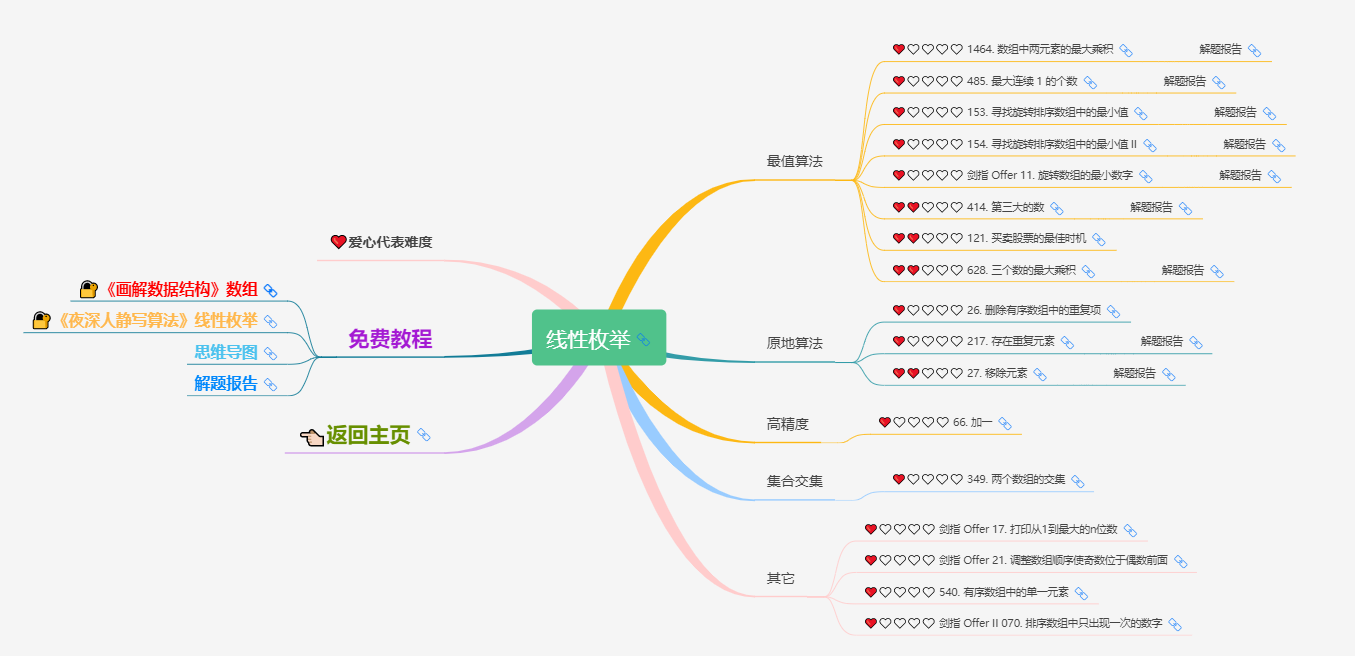
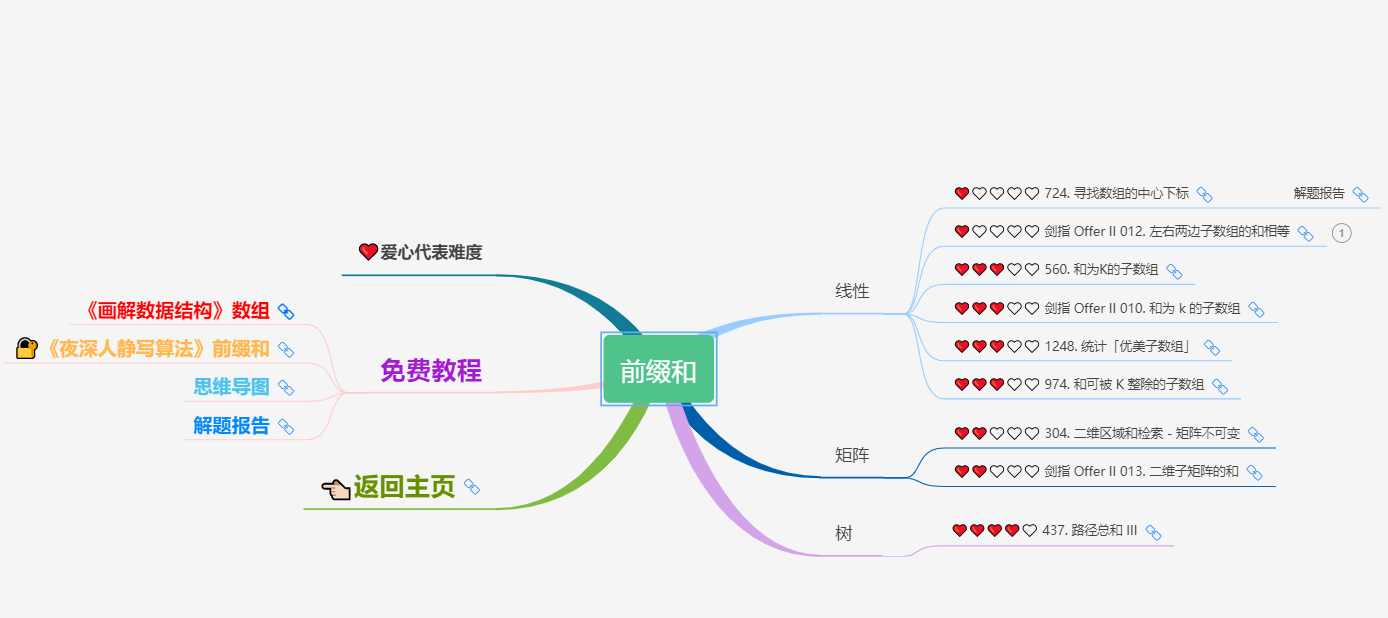
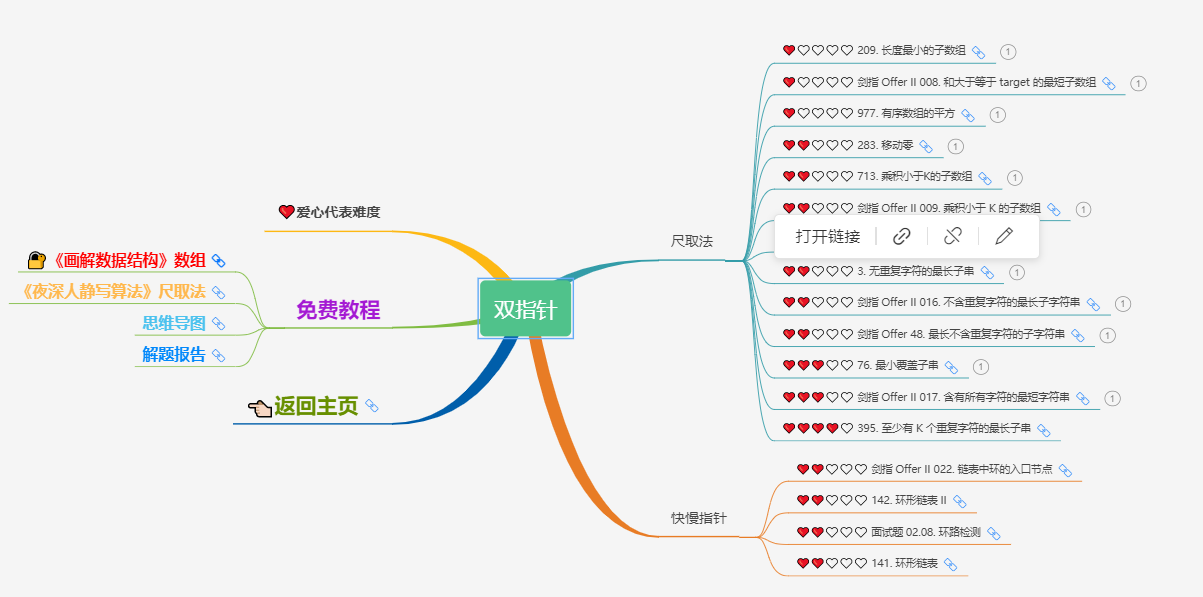
_To make this interesting and to take care of beginners, only the simplest algorithm, Enumeration Series, is currently open (including linear enumeration, double pointer, prefix and, binary enumeration, three-thirds enumeration), when half of the members have finished brushing Enumeration Series.After all the questions, the next chapter opens, and when the set is finished and you're still in the group, you'll become a member of the Expert Group on the "Late Night People's Still Writing Algorithm".
_Don't underestimate this panel of experts. After three years, you'll be the last one to be seen. If you want to join, contact me. Considering that everyone is a student and that you don't have a "primary source of income", you won't ask for anything on your way to becoming God.
_🔥Contact the author, or sweep the 2-D code of the author's home page into groups, so join the list of brushing titles🔥
C language free animation tutorial, punch in with me! 🌞Guangtianhua Japanese Language C🌞
A Summary of C Language Topics at the Beginner Level 🧡100 Cases of Introduction to C Language🧡
Several kinematics learn a data structure 🌳Understanding Data Structure🌳
Group Learning, Group Growth 🌌Guidelines to Getting Started with Algorithms🌌
Competitor Golden Text Tutorial 💜Late Night Still Writing Algorithm💜