1 Preface
Programming problem: input an integer n and output the nth item of Fibonacci sequence
Some interviewers like to ask this question. Maybe you think it's too simple. It can be realized at once by recursion or recursion.
Just when you are full of confidence and realize it in two ways
Interviewer: now please optimize your recursive implementation with "tail recursion" and your recursive implementation with "ES6 deconstruction assignment"
...
At this time, if your basic skills are not solid, you may be confused.
It's such a simple question, which contains quite a lot of JS knowledge points. Especially in its optimization process, you can see that your basic skills are not solid, so some interviewers like to ask this question.
Let's look at recursive and recursive implementations and their respective optimization processes
2 recursion and tail recursion
2.1 recursive implementation
Let's start with recursive implementation:
function fibonacci(n) {
if (n === 0 || n === 1) {
return n;
}
return fibonacci(n - 1) + fibonacci(n - 2);
}
Let's see what's wrong with this code
The first problem is easy to see. When n is very large, the recursion depth is too large, resulting in stack memory overflow, that is, "burst stack"
The second problem is that there are quite a lot of repeated calculations, such as:
fibonacci(7) = fibonacci(6) + fibonacci(5) // Here we calculate f(5), and next we calculate f(5) = (fibonacci(5) + fibonacci(4)) + (fibonacci(4) + fibonacci(3)) // Here, f(5) is calculated twice ...
2.2 tail call
Before solving the above two problems, let's take a look at what tail calls are
Tail call: the last action in a function is to return the call result of a function, that is, the return value of the new call in the last step is returned by the current function
For example:
function f(x) {
return g(x)
}
The following situations are not tail calls:
function f(x) {
return g(x) + 1 // First execute g(x), and finally return the return value of g(x) + 1
}
function f(x) {
let ret = g(x) // Executed g(x) first
return ret // Finally, return the return value of g(x)
}
2.3 tail call elimination (tail call optimization)
When a function is called, the JS engine will create a new stack frame and push it to the top of the call stack to represent the function call
When a function call occurs, the computer must "remember" the location of the calling function - the return location, before it can return to the location with the return value at the end of the call. The return location is generally saved on the call stack.
In the special case of tail call, the computer theoretically does not need to remember the location of the tail call, but directly returns the return location of the current function with the return value from the called function (equivalent to directly returning twice in a row)
As shown in the following figure: due to the tail call, in theory, you can return directly from function g to position 1 (i.e. the return position of function f) without remembering position 2
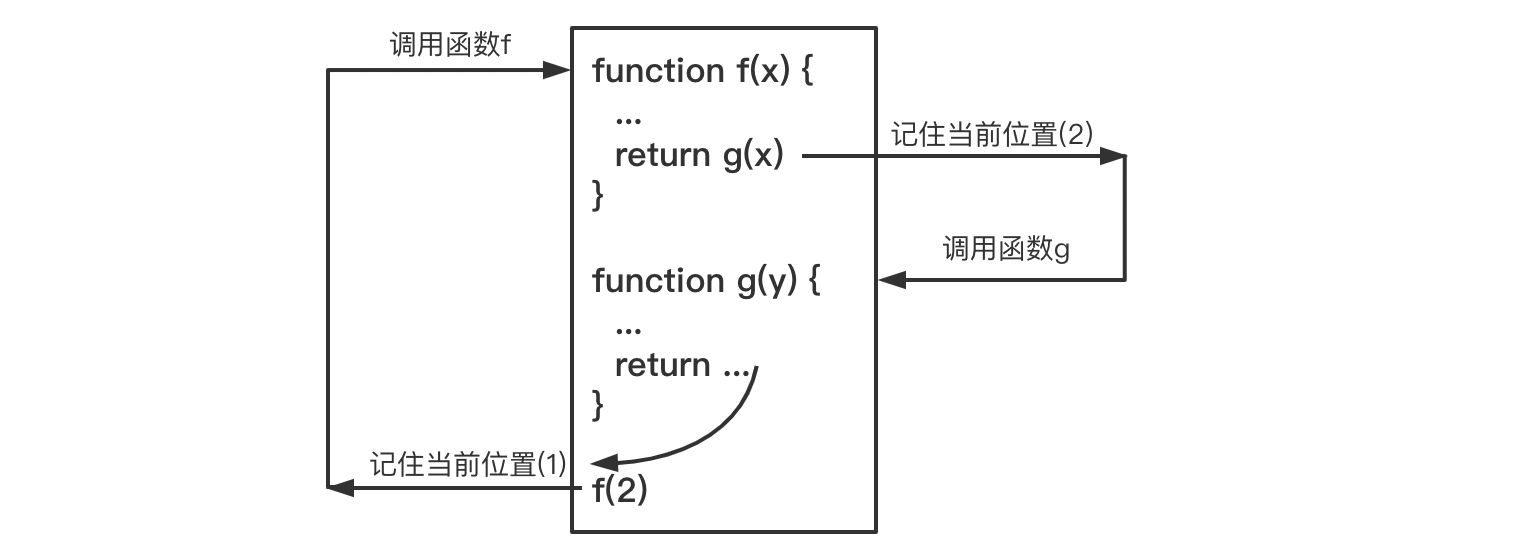
Since the work before the tail call has been completed, most of the things including local variables on the current function frame (i.e. the stack frame created during the call) are not needed. After appropriate changes, the current function frame can be directly used as the frame of the tail call function, and then the program can jump to the function called by the tail.
Use the example in the above figure to explain that the work before calling function g at the end of function f has been completed, so the function frame created when calling function f is directly used by function g, so there is no need to re create the stack frame for function G.
The process of reusing function frame changes is called tail call elimination or tail call optimization
2.4 tail recursion
If the function calls itself at the tail call position, this is called tail recursion. Tail recursion is a special tail call, that is, calling its own recursive function directly at the tail
Due to the elimination of tail call, there is only one stack frame in tail recursion, so it will never "burst the stack".
ES6 stipulates that all ECMAScript implementations must deploy "tail call elimination". Therefore, as long as tail recursion is used in ES6, stack overflow will not occur
2.5 tail recursive optimization Fibonacci function
Back to the two problems of Fibonacci function in 2.1, tail recursion can be used to solve the problem of "stack explosion"
It should be noted that the tail call elimination of ES6 is only enabled in strict mode
In order to turn the original recursive function into tail recursion, you need to rewrite the function and let the function call itself in the last step
// Original recursive function
function fibonacci(n) {
if (n === 0 || n === 1) {
return n;
}
return fibonacci(n - 1) + fibonacci(n - 2);
}
// After modification
'use strict'
function fibonacci(n, pre, cur) {
if (n === 0) {
return n;
}
if (n === 1) {
return cur;
}
return fibonacci(n - 1, cur, pre + cur);
}
// call
fibonacci(6, 0, 1)
The modified calculation logic is as follows:
f(6, 0, 1) = f(5, 1, 0 + 1) = f(4, 1, 1 + 1) = f(3, 2, 1 + 2) = f(2, 3, 2 + 3) = f(1, 5, 3 + 5) = 8
You may have found that, in fact, this is recursion, starting from 0 + 1 to item n
In addition, you can use the default parameter of ES6 to let the function pass in only one parameter n
'use strict'
function fibonacci(n, pre = 0, cur = 1) {
if (n === 0) {
return n;
}
if (n === 1) {
return cur;
}
return fibonacci(n - 1, cur, pre + cur);
}
fibonacci(6)
In addition, because the function is changed to tail recursion, the f(n) is only related to f(n-1), and the problem of a large number of repeated calculations has also been solved
3 recurrence
Recursive implementation
function fibonacci(n) {
let cur = 0;
let next = 1;
for (let i = 0; i < n; i++) {
let temp = cur;
cur = next;
next += temp;
}
return cur;
}
Recursion doesn't have much to optimize in performance, but we can optimize it in form
Using the deconstruction assignment of ES6, intermediate variables can be omitted
function fibonacci(n) {
let cur = 0;
let next = 1;
for (let i = 0; i < n; i++) {
[cur, next] = [next, cur + next]
}
return cur;
}
Official account [front end]