This time, we will talk about simple index and matrix traversal.
Attached herewith Video link If you want to know more about it, you can have a look.

Introduction of numpy third party Library

First, we introduce numpy as a third-party library. If a classmate does not install numpy, he can install it from the command line (Mac user sudo pip3 install numpy)

import numpy as np

II. Index of Matrix

1. Index of one-dimensional matrix

A = np.arange(3, 15)
print(A[3]) # An index of a one-dimensional matrix that prints the third data of a sequence

2. Index of Two-Dimensional Matrix

B = np.arange(3, 15).reshape((3, 4))
print(B[2]) # Print out the second line of the matrix
print(B[2, :]) # Print out all the numbers on the second line and print out the same result as above.
print(B[:, 1]) # Print out all the numbers in the first column
print(B[1, 1:3]) # Print out the number of columns 1 to 3 in line 1 (left closed right open interval)
print(B[1][1]) # Index to the first row, first column of a matrix
print(B[1, 1]) # The same result.

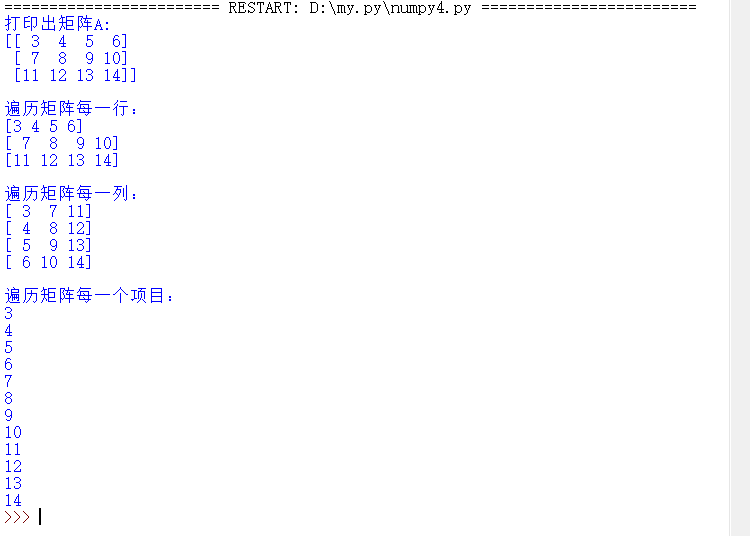
3. Traversal of Matrix

A = np.arange(3, 15).reshape((3, 4))
print(A)
for row in A:
   print(row) # Traversal matrix every row
for column in A.T:
   print(column) # Traverse each column of matrix A (A.T is to transpose the matrix)
for item in A.flat:
   print(item) # Traverse each item of a matrix (A.flat is to convert a matrix into a sequence)

Code examples

1. Index of Matrix

import numpy as np

B = np.arange(3, 15).reshape((3, 4))   # Define Matrix B of 3 Rows and 4 Columns
print('Print out the matrix B:')
print(B)
print('\n Print out the second line of the matrix:')
print(B[2])              
print('\n Print out the second line of the matrix. The effect is the same as above.:')      
print(B[2, :])                
print('\n Print out all the numbers in the first column of the matrix:')
print(B[:, 1])                
print('\n Print out the number of columns 1 to 3 in the first row of the matrix (left closed right open interval):')
print(B[1, 1:3])            
print('\n Index to the first row, first column of a matrix:')
print(B[1: 1])                

The operation results are as follows:

2. Traversal of Matrix

import numpy as np

A = np.arange(3, 15).reshape((3, 4))
print('Print out the matrix A:')
print(A)
print('\n Traversal matrix each row:')
for row in A:   
    print(row)  
print('\n Traversal matrix each column:')
for column in A.T:                #  A.T. Transpose Matrix
    print(column)  
print('\n Traversal matrix for each item:')
for item in A.flat:               #  A.flat is to transform a matrix into a sequence
    print(item)                

The operation results are as follows:

Okay, that's what the index of the matrix is related to traversal.

You are welcome to comment and leave a message or give suggestions below. If there are any mistakes, please point them out. I hope this blog can help the students who have just learned this, and welcome you to share it with those who need it.

If you need to reproduce, please indicate the source.