Introduction of Singular Value Decomposition
singular value decomposition (SVD) can be understood as: a more complex matrix is represented by the multiplication of three smaller and simpler sub-matrices, which describe the important characteristics of large matrices. SVD has many uses, such as LSA (implicit semantic analysis), recommendation system, data dimensionality reduction, signal processing and statistics.Assuming that A is a matrix of Mx N, M >= N, then A can be decomposed according to the following formula:
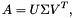
Among them, U is a standard orthogonal matrix of MxN, is a diagonal matrix of NxN and V is a standard orthogonal matrix of NxN. The diagonal elements on_are called singular values. This formula shows that the function of matrix A is to rotate a vector from the space of the orthogonal basis vectors of V to the space of the orthogonal basis vectors of U, and scale it in all directions according to_. The multiples of scaling are singular values.
2. Singular Value Decomposition Function of MADlib
The SVD function of MADlib can decompose dense matrix and sparse matrix by singular value factorization, and also provides a local high performance implementation function of sparse matrix.1. SVD Function of Dense Matrix
(1) Grammarsvd( source_table,
output_table_prefix,
row_id,
k,
n_iterations,
result_summary_table
);source_table: TEXT type, source table name (dense matrix). The table contains a row_id column identifying each row, starting with the number 1. The other columns contain the data of the matrix. You can use either of two dense formats, such as the 2x2 matrix in the following example.
Format 1:
row_id col1 col2
row1 1 1 0
row2 2 0 1
Format 2:
row_id row_vec
row1 1 {1, 0}
row2 2 {0, 1}row_id: TEXT type, ID for each row.
k: INTEGER type, the number of singular values calculated.
n_iterations (optional): INTEGER type, the number of iterations to run, must be within [k, column dimension], K is the number of singular values.
Results_summary_table (optional): TEXT type, which stores the name of the result summary table.
2. SVD Function of Sparse Matrix
Matrix represented in sparse format uses this function. For efficient computation, input matrices are converted to dense matrices before singular value decomposition (SVD) operations.(1) Grammar
svd_sparse( source_table,
output_table_prefix,
row_id,
col_id,
value,
row_dim,
col_dim,
k,
n_iterations,
result_summary_table
);source_table: TEXT type, source table name (sparse matrix). Sparse matrices use row and column subscripts to indicate each non-zero entry of the matrix, which is very suitable for matrices with many zero elements. In the 4x7 matrix shown below, there are only six rows of zeros removed. The dimensions of matrices are derived from the maximum values of rows and columns. Note that the last line, even 0, contains this line, because it identifies the dimensions of the matrix and implies that rows 4 and 7 are all zero.
row_id | col_id | value
--------+--------+-------
1 | 1 | 9
1 | 5 | 6
1 | 6 | 6
2 | 1 | 8
3 | 1 | 3
3 | 2 | 9
4 | 7 | 0
(6 rows)row_id: TEXT type, containing column names with row subscripts.
col_id: TEXT type, containing column names with column subscripts.
Value: TEXT type, containing the column name of the value.
row_dim: INTEGER type, the number of rows of a matrix.
col_dim: INTEGER type, number of columns of a matrix.
k: INTEGER type, the number of singular values calculated.
n_iterations (optional): INTEGER type, the number of iterations to run, must be within [k, column dimension], K is the number of singular values.
Results_summary_table (optional): TEXT type, which stores the name of the result summary table.
3. Local Implementation of SVD Function for Sparse Matrix
This function uses local sparse representation when calculating SVD. It can calculate sparse matrices more efficiently and is suitable for highly sparse matrices.(1) Grammar
svd_sparse_native( source_table,
output_table_prefix,
row_id,
col_id,
value,
row_dim,
col_dim,
k,
n_iterations,
result_summary_table
);Parametric meaning is the same as svd_sparse function.
4. Output table
The output of the SVD function is the following three tables:- Left Singular Value Matrix: The table name is <output_table_prefix>_u.
- Left Singular Value Matrix: The table name is <output_table_prefix>_v.
- Singular value: The table name is <output_table_prefix>_s.
row_id INTEGER type. The ID corresponding to each eigenvalue.
row_vec FLOAT8[] type. The row_id corresponds to the eigenvector element with an array size of k.
Since only the diagonal elements are non-zero, the singular value table is sparsely tabulated:
row_id INTEGER type, the first singular value is i.
col_id INTEGER type, the first singular value is i (same as row_id).
Value FLOAT8 type, singular value.
The row_id and col_id in the table above all start from 1.
The results summary table names are as follows:
rows_used INTEGER type, SVD calculates the number of rows used.
Exc_time FLOAT8 type calculates the total time used by SVD.
iter INTEGER type, number of iterations.
recon_error FLOAT8 type, the quality score of this set of orthogonal bases (such as approximate accuracy). The calculation formula is formula 2.
relative_recon_error FLOAT8 type, relative mass fraction. The calculation formula is formula 3.
5. Online Help
select madlib.svd();
-- usage
select madlib.svd('usage');
-- Example
select madlib.svd('example');3. An Example of Recommended Algorithms for Singular Value Decomposition Function Implementation
Using sparse SVD functions to solve the problem of music recommendation introduced in the previous article, see“ MADlib(2) Implementation of Recommendation Algorithms by Low Rank Matrix Decomposition in Data Mining with SQL Play" .1. Establishing an input table
(1) Establishing Index TableAs can be seen from the previous explanation, the row and column subscripts of the recommendation matrix represent users and music works respectively. However, in business systems, userid and musicid are probably not generated in the order of rules from 0 to N. Therefore, it is necessary to establish the mapping relationship between matrix subscripts and business table ID s. Here, the BIGSERIAL self-increasing data type of HAWQ is used to correspond to the index subscripts of the recommendation matrix.
-- User Index Table drop table if exists tbl_idx_user; create table tbl_idx_user (user_idx bigserial, userid varchar(10)); -- Music Index Table drop table if exists tbl_idx_music; create table tbl_idx_music (music_idx bigserial, musicid varchar(10));
(2) Establishing User Behavior Table
drop table if exists mat; create table mat ( row_id int, col_id int, val float8 );
2. Generating input table data
-- User table
insert into tbl_idx_user (userid)
values ('u1'),('u2'),('u3'),('u4'),('u5'),('u6'),('u7'),('u8'),('u9'),('u10'),('u11'),('u12'),('u13'),('u14'),('u15'),('u16'),('u17'),('u18'),('u19');
-- Music table
insert into tbl_idx_music (musicid)
values ('m1'),('m2'),('m3'),('m4'),('m5'),('m6'),('m7'),('m8'),('m9'),('m10'),('m11'),('m12'),('m13');
-- User Behavior Table
insert into mat values (1, 1, 5), (1, 6, -5), (1, 9, 5), (1, 10, 3), (1, 12, 1), (1, 13, 5);
insert into mat values (2, 4, 3), (2, 9, 3), (2, 13, 4);
insert into mat values (3, 3, 1), (3, 5, 2), (3, 6, -5), (3, 7, 4), (3, 10, -2), (3, 11, -2), (3, 13, -2);
insert into mat values (4, 2, 4), (4, 3, 4), (4, 4, 3), (4, 7, -2), (4, 9, -5), (4, 12, 3);
insert into mat values (5, 2, 5), (5, 3, -5), (5, 5, -5), (5, 7, 4), (5, 8, 3), (5, 11, 4);
insert into mat values (6, 3, 4), (6, 6, 3), (6, 9, 4);
insert into mat values (7, 2, -2), (7, 6, 5), (7, 10, 4), (7, 12, 4), (7, 13, -2);
insert into mat values (8, 2, -2), (8, 6, 5), (8, 8, 5), (8, 10, 4), (8, 13, -2);
insert into mat values (9, 6, 4), (9, 11, 5);
insert into mat values (10, 4, 3), (10, 6, 4), (10, 11, 3);
insert into mat values (11, 5, 4), (11, 8, 1), (11, 10, 4);
insert into mat values (12, 1, 3), (12, 2, 1), (12, 3, 4), (12, 8, 2), (12, 9, 2) ;
insert into mat values (13, 1, 5), (13, 2, 4), (13, 3, 5), (13, 8, 5), (13, 9, 5) ;
insert into mat values (14, 5, 5), (14, 7, 1), (14, 10, 5) ;
insert into mat values (15, 1, 4), (15, 2, 3), (15, 3, 4), (15, 8, 5), (15, 9, 5), (15, 11, 1) ;
insert into mat values (16, 4, 4), (16, 6, 4), (16, 11, 4) ;
insert into mat values (17, 4, 2), (17, 6, 2), (17, 7, 5), (17, 10, 1), (17, 11, 2) ;
insert into mat values (18, 5, 5), (18, 10, 4) ;
insert into mat values (19, 1, 1), (19, 8, 1), (19, 9, 2) ;3. Call svd_sparse function
drop table if exists svd_u;
drop table if exists svd_v;
drop table if exists svd_s;
drop table if exists svd_summary;
select madlib.svd_sparse( 'mat', -- input table
'svd', -- output table prefix
'row_id', -- column name with row index
'col_id', -- column name with column index
'val', -- matrix cell value
19, -- number of rows in matrix
13, -- number of columns in matrix
13, -- number of singular values to compute
NULL, -- Use default number of iterations
'svd_summary' -- Result summary table
);4. Matrix Multiplication to Generate Recommendation Matrix
Similar to the low-rank matrix decomposition algorithm used in the previous article, in recommendation system, after SVD processing of the matrix, we extract the most critical singular value, and do not reconstruct the matrix for use, directly multiply the U matrix or V matrix to get the recommendation matrix.drop table if exists mat_r;
select madlib.matrix_mult('svd_u', 'row=row_id, val=row_vec',
'svd_v', 'row=row_id, val=row_vec, trans=true',
'mat_r');drop table if exists mat_r_sparse;
select madlib.matrix_sparsify('mat_r', 'row=row_id, val=row_vec',
'mat_r_sparse', 'col=col_id, val=val');select t2.userid,t3.musicid,t1.val
from (select row_id,col_id,val,row_number() over (partition by row_id order by val desc) rn
from mat_r_sparse t1
where not exists (select 1 from mat t2
where t1.row_id = t2.row_id and t1.col_id = t2.col_id)) t1,
tbl_idx_user t2, tbl_idx_music t3
where t1.rn = 1 and t2.user_idx= t1.row_id and t3.music_idx = t1.col_id
order by t2.user_idx;userid | musicid | val --------+---------+-------------------- u1 | m11 | 0.17459952742497 u2 | m8 | 0.189675012677457 u3 | m12 | 0.231338446896519 u4 | m13 | 0.106841900389706 u5 | m10 | 0.162711426419817 u6 | m10 | 0.184495296529734 u7 | m9 | 0.125433703315066 u8 | m4 | 0.0584897976113909 u9 | m13 | 0.214993320202223 u10 | m1 | 0.177930632546576 u11 | m11 | 0.0803502883654762 u12 | m7 | 0.0742119481427605 u13 | m6 | 0.193742876218372 u14 | m2 | 0.159209534273547 u15 | m12 | 0.105695455132407 u16 | m9 | 0.1012699016073 u17 | m13 | 0.195197867121742 u18 | m2 | 0.161086589735508 u19 | m12 | 0.0784852961643377 (19 rows)