What is a binary search tree? What are the characteristics of binary search tree? How to implement binary search tree?

1: Binary search tree is also called binary search tree and binary sort tree. As the name suggests, the search efficiency of binary search tree is very high, and binary search tree should meet the structural characteristics of binary tree, so each root node has only two leaf nodes at most. This binary search tree is similar to the heap structure learned earlier.

Image structure of the tree:

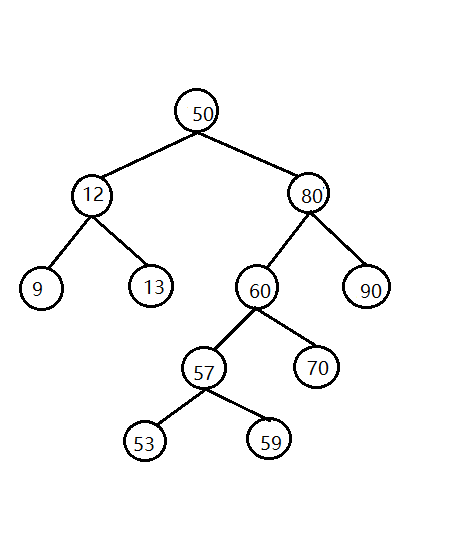
  2: Characteristics of binary search tree: it can be seen from the above binary tree structure image that the value of the left child node is smaller than the root node, and the value of the right child node is larger than the root node. This is the characteristic of search binary tree.

1) If the left subtree is not empty, the values of all nodes on the left subtree are less than or equal to the values of its root node;

2) If the right subtree is not empty, the values of all nodes on the right subtree are greater than or equal to the values of its root node;

3) The left and right subtrees are also binary sort trees

3: Implementation of binary search tree

The construction of binary search tree is also built according to its characteristics. The constructed binary search tree should connect each child node to the parent node, so two pointers should be defined, one is the right child node, the pointer points to the right word node, and the other is the left child node, the pointer points to the left child node.

Code implementation:

typedef struct binaryTree {
	elemStyle date;
	struct binaryTree* leftChild;
	struct binaryTree* rightChild;
}Btree;

After the structure of the representation tree is defined, what we need to do is to build a binary search tree

//Insert node in binary search tree
bool insertBinaryTree(Btree** root, Btree* node) {
	Btree* tmp, * father = NULL;
	if (!node) {
		return false;//The node has no memory allocated
	}
	else {
		node->leftChild = NULL;
		node->rightChild = NULL;
	}

	if (*root) {
		tmp = *root;
	}
	else {
		*root = node;
		return true;
	}

	while (tmp) {
		father = tmp;
		if (compare(tmp->date, node->date)) {
			tmp = tmp->rightChild;
		}
		else {
			tmp = tmp->leftChild;
		}
	}
	if (compare(father->date, node->date)) {
		father->rightChild = node;
	}
	else {
		father->leftChild = node;
	}
	return true;
}

Construction idea: according to the characteristics of binary search tree, the left word node must be less than or equal to the root node, and the right word node must be greater than or equal to the root node. If there is no root node, take the first node as the root node and return it. If there is a root node, judge which value of the root node and the node entering the tree is greater. If the value of the root node is greater than the current value, lock it to the right node, otherwise lock it to the left child node, and continue cyclic comparison until the child node pointed to by the root node is empty, Connect the current node to the root node, and the new node in the tree does the same.

After the tree construction is completed, the traversal tree should be left. We use stack to realize the implementation of preorder traversal tree

//Preorder traversal binary tree
void ergodicBinaryTree(Btree* root) {
	if (!root)return;
	Stack stack;
	initStack(stack);
	Btree tmp;
	enterStack(stack, *root);
	cout << "The elements in the tree are:";

	while (stack.top != stack.base) {
		outStack(stack, tmp);
		cout << tmp.date << "  ";
		if (tmp.rightChild) {
			enterStack(stack, *tmp.rightChild);
		}
		if (tmp.leftChild) {
			enterStack(stack, *tmp.leftChild);
		}
	}
	destoryStack(stack);
}

Specific ideas for implementation:

The tree structure has been built before, so the first step is to put the first node into the stack, judge whether its two child nodes are empty, put the nodes that are not empty into the stack, cycle in turn, and then put the last node out of the stack, and then judge whether the child nodes of the node are empty. If they are not empty, continue to put into the stack. This operation can realize the printing of tree species elements

Delete the nodes in the tree and implement recursively, so if you want to understand this operation, you should understand recursion

//Delete node of tree
Btree* deleteBinaryTree(Btree* root, elemStyle index, Btree*& node) {
	//This node does not exist in the tree
	if (root == NULL)return NULL;
	if (compare(root->date, index)) {
		root->rightChild = deleteBinaryTree(root->rightChild, index, node);
		return root;
	}
	if (compare(index, root->date)) {
		root->leftChild = deleteBinaryTree(root->leftChild, index, node);
		return root;
	}
	node = root;
	//The left and right child nodes are empty
	if (!root->leftChild && !root->rightChild)return NULL;
	//The left node is empty and the right node is not empty
	if (!root->leftChild && root->rightChild)return root->rightChild;
	//The right node is empty and the left node is not empty
	if (!root->rightChild && root->leftChild)return root->leftChild;
	//Both left and right nodes are not empty
	root->date = findBinaryTree(root->leftChild);
	root->leftChild = deleteBinaryTree(root->leftChild, root->date, node);
	return root;
}

//Maximum node found
elemStyle findBinaryTree(Btree* node) {
	while (node->rightChild) {
		node = node->rightChild;
	}
	return node->date;
}

Since the logic of this operation is complex, it will not be explained

Data body code implementation

#pragma once
#include<iostream>

using namespace std;

typedef int elemStyle;
#define MAX_SIZE 28

typedef struct binaryTree {
	elemStyle date;
	struct binaryTree* leftChild;
	struct binaryTree* rightChild;
}Btree;

typedef struct _stack {
	Btree* top;
	Btree* base;
}Stack;

bool initStack(Stack& stack); //Initialization stack
void enterStack(Stack& stack, Btree treeNode);//Stack elements
void outStack(Stack& stack, Btree& tree);//Stack elements
void destoryStack(Stack& stack);//Destroy stack

//Initialization stack
bool initStack(Stack& stack) {
	stack.base = new Btree[MAX_SIZE];
	if (!stack.base)return false;
	stack.top = stack.base;
	return true;
}

//Stack elements
void enterStack(Stack& stack, Btree treeNode) {
	if (stack.top - stack.base == MAX_SIZE)return;
	*(stack.top++) = treeNode;
	return;
}

//Stack elements
void outStack(Stack& stack, Btree& tree) {
	if (stack.top == stack.base)return;
	tree = *(--stack.top);
	return;
}

//Destroy stack
void destoryStack(Stack& stack) {
	if (stack.base) {
		delete stack.base;
		stack.top = NULL;
		stack.base = NULL;
	}
}

#pragma once
#include"_stack.h"

#define compare(a,b) (a < b)
#define equal(a,b) (a == b)

bool insertBinaryTree(Btree** root, Btree* node);//Insert node in binary search tree
void ergodicBinaryTree(Btree* root);//Traversal binary tree
Btree* deleteBinaryTree(Btree* root, elemStyle index, Btree*& node);//Delete node of tree
elemStyle findBinaryTree(Btree* node);//Maximum node found

//Insert node in binary search tree
bool insertBinaryTree(Btree** root, Btree* node) {
	Btree* tmp, * father = NULL;
	if (!node) {
		return false;//The node has no memory allocated
	}
	else {
		node->leftChild = NULL;
		node->rightChild = NULL;
	}

	if (*root) {
		tmp = *root;
	}
	else {
		*root = node;
		return true;
	}

	while (tmp) {
		father = tmp;
		if (compare(tmp->date, node->date)) {
			tmp = tmp->rightChild;
		}
		else {
			tmp = tmp->leftChild;
		}
	}
	if (compare(father->date, node->date)) {
		father->rightChild = node;
	}
	else {
		father->leftChild = node;
	}
	return true;
}

//Preorder traversal binary tree
void ergodicBinaryTree(Btree* root) {
	if (!root)return;
	Stack stack;
	initStack(stack);
	Btree tmp;
	enterStack(stack, *root);
	cout << "The elements in the tree are:";

	while (stack.top != stack.base) {
		outStack(stack, tmp);
		cout << tmp.date << "  ";
		if (tmp.rightChild) {
			enterStack(stack, *tmp.rightChild);
		}
		if (tmp.leftChild) {
			enterStack(stack, *tmp.leftChild);
		}
	}
	destoryStack(stack);
}

//Delete node of tree
Btree* deleteBinaryTree(Btree* root, elemStyle index, Btree*& node) {
	//This node does not exist in the tree
	if (root == NULL)return NULL;
	if (compare(root->date, index)) {
		root->rightChild = deleteBinaryTree(root->rightChild, index, node);
		return root;
	}
	if (compare(index, root->date)) {
		root->leftChild = deleteBinaryTree(root->leftChild, index, node);
		return root;
	}
	node = root;
	//The left and right child nodes are empty
	if (!root->leftChild && !root->rightChild)return NULL;
	//The left node is empty and the right node is not empty
	if (!root->leftChild && root->rightChild)return root->rightChild;
	//The right node is empty and the left node is not empty
	if (!root->rightChild && root->leftChild)return root->leftChild;
	//Both left and right nodes are not empty
	root->date = findBinaryTree(root->leftChild);
	root->leftChild = deleteBinaryTree(root->leftChild, root->date, node);
	return root;
}

//Maximum node found
elemStyle findBinaryTree(Btree* node) {
	while (node->rightChild) {
		node = node->rightChild;
	}
	return node->date;
}