Implement lock striping
Concurrent HashMap allows multiple modification operations to be performed concurrently. The key is to use lock separation technology. It uses multiple locks to control changes to different parts of the hash table. Concurrent HashMap uses segments to represent these different parts. Each segment is actually a small hash table, which has its own lock. As long as multiple modification operations occur on different segments, they can be performed concurrently.
Some methods need to span segments, such as size() and containsValue(). They may need to lock the entire table instead of just one segment. This requires locking all segments in order. After the operation, the locks of all segments are released in order. Here "in order" is very important, otherwise deadlock may occur. In the ConcurrentHashMap, the segment array is final, and its member variables are actually final. However, just declaring the array as final does not guarantee that the array members are final, which needs to be implemented. This ensures that deadlocks do not occur because the order in which locks are acquired is fixed. Invariance is very important for multithreaded programming. I will talk about it next.
/**
* The segments, each of which is a specialized hash table
*/
final Segment<K,V>[] segments;
//From the comments in this code, we can see that each node is a hashtable that will be synchronized in the future.Immutable and volatile
ConcurrentHashMap fully allows multiple read operations to be performed concurrently, and the read operation does not need to be locked. If we use the traditional technology, such as the implementation in HashMap, and allow to add or delete elements in the middle of the hash chain, the read operation will get inconsistent data without locking. The implementation technology of concurrent HashMap ensures that the HashEntry is almost immutable. HashEntry represents a node in each hash chain, and its structure is as follows:
static final class HashEntry<K,V> {
final K key;
final int hash;
volatile V value;
final HashEntry<K,V> next;
}
It can be seen that except value is not final, other values are final, which means that nodes cannot be added or deleted from the middle or tail of the hash chain, because this requires modifying the next reference value, and all nodes can only be modified from the head. For put operations, you can always add them to the head of the hash chain.
However, for the remove operation, you may need to delete a node from the middle, which requires copying all the previous nodes of the node to be deleted, and the last node points to the next node of the node to be deleted. This is similar to the deletion of linked list in data structure.
To ensure that the read operation can see the latest value, set value to volatile, which avoids locking.
The article that follows the volatile keyword explains that it works like synchronized.Other
In order to speed up the speed of locating the segment and the hash slots in the segment, the number of hash slots in each segment is 2^n, which makes it possible to locate the position of the segment and the hash slots in the segment by bit operation. When the concurrency level is the default value of 16, which is the number of segments, the high 4 bits of the hash value determine which segment to allocate. But let's not forget the lesson from the introduction to algorithms: the number of hash slots should not be 2^n, which may lead to uneven allocation of hash slots, which needs to be hashed again.
The following is the algorithm of heavy hash:
private static int hash(int h) {
// Spread bits to regularize both segment and index locations,
// using variant of single-word Wang/Jenkins hash.
h += (h << 15) ^ 0xffffcd7d;
h ^= (h >>> 10);
h += (h << 3);
h ^= (h >>> 6);
h += (h << 2) + (h << 14);
return h ^ (h >>> 16);
}Here is how to locate the end:
final Segment<K,V> segmentFor(int hash) {
return segments[(hash >>> segmentShift) & segmentMask];
}data structure
As for the basic data structure of Hash table, it is actually the form of array ➕ linked list. There are not too many details about the basic attributes and operations of array and linked list.
One of the most important aspects of hash table is how to solve the hash conflict. We have learned in the data structure, and then hash method, zipper method and other hash conflict processing methods. These methods will be introduced in the data structure module later.
ConcurrentHashMap and HashMap use the same method, both of which put nodes with the same hash value in a hash chain. Unlike HashMap, ConcurrentHashMap uses multiple child hash tables, that is, segments. Here are the data members of ConcurrentHashMap:
public class ConcurrentHashMap<K, V> extends AbstractMap<K, V>
implements ConcurrentMap<K, V>, Serializable {
/**
* Mask value for indexing into segments. The upper bits of a
* key's hash code are used to choose the segment.
*/
final int segmentMask;
/**
* Shift value for indexing within segments.
*/
final int segmentShift;
/**
* The segments, each of which is a specialized hash table
*/
final Segment<K,V>[] segments;
}
//All members are final, and segmentMask and segmentShift are mainly used to locate segments.Each Segment is equivalent to a child Hash table. Its data members are as follows:
static final class Segment<K,V> extends ReentrantLock implements Serializable {
private static final long serialVersionUID = 2249069246763182397L;
/**
* The number of elements in this segment's region.
*/
transient volatile int count;
/**
* Number of updates that alter the size of the table. This is
* used during bulk-read methods to make sure they see a
* consistent snapshot: If modCounts change during a traversal
* of segments computing size or checking containsValue, then
* we might have an inconsistent view of state so (usually)
* must retry.
*/
transient int modCount;
/**
* The table is rehashed when its size exceeds this threshold.
* (The value of this field is always <tt>(int)(capacity *
* loadFactor)</tt>.)
*/
transient int threshold;
/**
* The per-segment table.
*/
transient volatile HashEntry<K,V>[] table;
/**
* The load factor for the hash table. Even though this value
* is same for all segments, it is replicated to avoid needing
* links to outer object.
* @serial
*/
final float loadFactor;
}
1,count It is used to count the number of data in this segment. volatile,It is used to coordinate the modification and reading operations, so as to ensure that the read operation can read almost the latest modification of the data.
//The coordination method is as follows: when the structure of each modification is changed, such as adding / deleting nodes (modifying the value of nodes does not count the structural change), the count value should be written, and the count value should be read at the beginning of each read operation. This takes advantage of Java 5's semantic enhancement of volatile, and there is a "happens before" relationship between the writing and reading of the same volatile variable.
2,modCount Statistics of the number of segment structure changes is mainly to detect whether a segment changes in the process of traversing multiple segments, which will be described in detail when describing cross segment operations.
3,threashold Used to indicate the need for rehash The limit value of.
5,table Array storage segment nodes, each array element is a hash Chain, use HashEntry Express. table Also volatile,This allows you to read the latest table Value without synchronization.
6,loadFactor Represents the load factor.Implementation details
Modify operation
First, let's take a look at the delete operation remove(key).
public V remove(Object key) {
int hash = hash(key.hashCode());
return segmentFor(hash).remove(key, hash, null);
}
//The whole operation is to locate the segment first and then delegate to the segment's remove operation. When multiple deletion operations occur simultaneously, as long as the segment they are in
//Different, they can be done at the same time. The following is the implementation of Segment's remove method:
V remove(Object key, int hash, Object value) {
lock();
try {
int c = count - 1;
HashEntry<K,V>[] tab = table;
int index = hash & (tab.length - 1);
HashEntry<K,V> first = tab[index];
HashEntry<K,V> e = first;
while (e != null && (e.hash != hash || !key.equals(e.key)))
e = e.next;
V oldValue = null;
if (e != null) {
V v = e.value;
if (value == null || value.equals(v)) {
oldValue = v;
// All entries following removed node can stay
// in list, but all preceding ones need to be
// cloned.
++modCount;
HashEntry<K,V> newFirst = e.next;
for (HashEntry<K,V> p = first; p != e; p = p.next)
newFirst = new HashEntry<K,V>(p.key, p.hash,
newFirst, p.value);
tab[index] = newFirst;
count = c; // write-volatile
}
}
return oldValue;
} finally {
unlock();
}
}
//The whole operation is performed when the segment lock is held. The line before the blank line is mainly located to the node e to be deleted.
//Next, if this node does not exist, null will be returned directly. Otherwise, the node in front of e will be copied once, and the tail node will point to the next node of E.
//The nodes behind e do not need to be copied, they can be reused.
//In fact, it is the deletion of linked list. If you have studied the data structure, you can easily understand it.
//Generally speaking, there are three nodes:
1,To delete the middle node, you only need to point the tail pointer of the first node to the third node (of course, the operation of the two-way linked list is not the same, but also the order of the design operation, so we won't do too much elaboration here)
2, To delete the first node, just point the head pointer to the first node.
3,To delete the third node (tail node), you only need to set the pointer of the previous node of the tail node to null. Here is a simple diagram of deleting nodes:
Before deleting a node:

After deleting element 3:
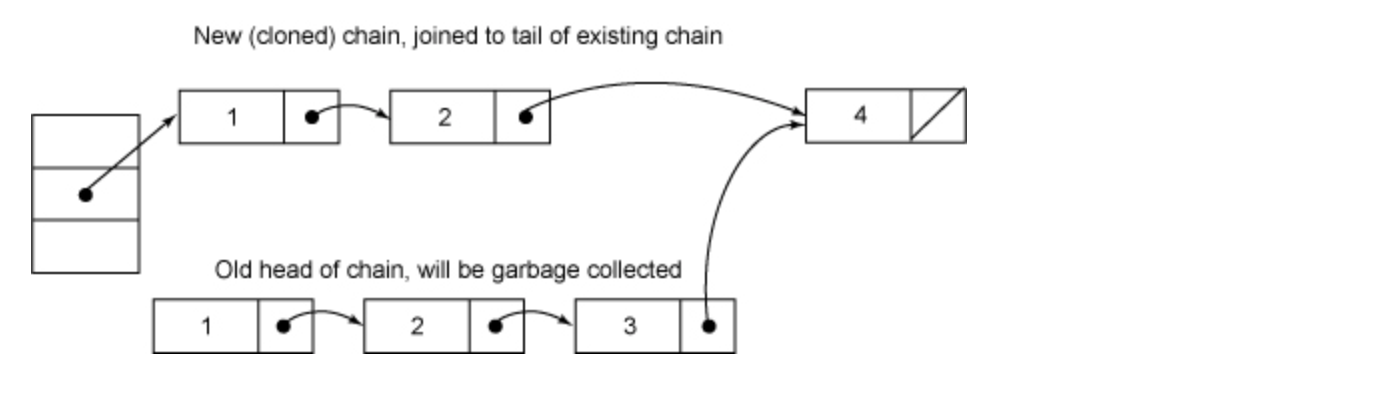
The whole implementation of remove is not complicated, but you need to pay attention to the following points. First, when the node to be deleted exists, the last step of deletion is to reduce the value of count by one. This must be the last step, or the read operation may not see the structural changes made to the segment previously. Second, at the beginning of the remove execution, the table is assigned to a local variable tab. This is because the table is a volatile variable, so it is very expensive to read and write the volatile variable. The compiler can't do any optimization on the reading and writing of volatile variables. It doesn't have much influence on accessing non volatile instance variables many times directly. The compiler will do corresponding optimization.
Next, let's look at the put operation, which is also the put method delegated to the segment. Here is the put method of the segment:
V put(K key, int hash, V value, boolean onlyIfAbsent) {
lock();
try {
int c = count;
if (c++ > threshold) // ensure capacity determines whether expansion is needed
rehash();
HashEntry<K,V>[] tab = table;
int index = hash & (tab.length - 1);
HashEntry<K,V> first = tab[index];
HashEntry<K,V> e = first;
while (e != null && (e.hash != hash || !key.equals(e.key)))
e = e.next;
V oldValue;
if (e != null) {
oldValue = e.value;
if (!onlyIfAbsent)
e.value = value;
}
else {
oldValue = null;
++modCount;
tab[index] = new HashEntry<K,V>(key, hash, first, value);
count = c; // write-volatile
}
return oldValue;
} finally {
unlock();
}
}
//This method is also implemented when the segment lock is held. First, determine whether rehash is needed, and then rehash is needed. Then it is to find out whether there is a node with the same key. If there is one, replace the value of the node directly. Otherwise, create a new node and add it to the head of the hash chain. At this time, you must modify the values of modCount and count, and also the value of count in the last step. put method calls rehash method, and reach method is also very ingenious. It mainly uses the size of table as 2^n, which will not be introduced here.
//The modification operations include putAll and replace. putAll is to call put method many times, nothing to say. Replace doesn't even need to make structural changes. The implementation is much simpler than put and delete. If you understand put and delete, you can understand replace. I won't introduce it here.Acquisition operation
First, let's look at the get operation. Similarly, the get operation of ConcurrentHashMap is directly delegated to the get method of Segment. Let's look at the get method of Segment directly:
V get(Object key, int hash) {
if (count != 0) { // read-volatile
HashEntry<K,V> e = getFirst(hash);
while (e != null) {
if (e.hash == hash && key.equals(e.key)) {
V v = e.value;
if (v != null)
return v;
return readValueUnderLock(e); // recheck
}
e = e.next;
}
}
return null;
}The get operation does not require a lock. The first step is to access the count variable, which is a volatile variable. Because all the modification operations will write the count variable in the last step when they modify the structure, this mechanism ensures that the get operation can get almost the latest structure update. For unstructured update, that is, the change of node value, because the value variable of HashEntry is volatile, the latest value can also be read. The next step is to traverse the hash chain to find the node to get. If not, directly access null. The reason why there is no need to lock when traversing the hash chain is that the chain pointer next is final. But the header pointer is not final, which is returned through getFirst(hash) method, that is, the value in the table array. This makes it possible for getFirst(hash) to return outdated header nodes. For example, when executing the get method, just after executing getFirst(hash), another thread performs the delete operation and updates the header node, which results in that the returned header node in the get method is not up-to-date. This allows get to read almost the latest data through the coordination mechanism of count variable, although it may not be the latest. To get the latest data, only complete synchronization is used.
Finally, if the node is found, the value will be returned directly if it is not empty. Otherwise, it will be read again in the locked state. This seems to be a little confusing. In theory, the value of a node cannot be empty. This is because the judgment is made when putting. If it is empty, NullPointerException will be thrown. The only source of null value is the default value in HashEntry. Because the value in HashEntry is not final, it is possible to read null value in asynchronous reading. Take a closer look at the statement of put operation: tab[index] = new HashEntry
V readValueUnderLock(HashEntry<K,V> e) {
lock();
try {
return e.value;
} finally {
unlock();
}
}Another operation is containsKey. This implementation is much simpler because it does not need to read the value:
boolean containsKey(Object key, int hash) {
if (count != 0) { // read-volatile
HashEntry<K,V> e = getFirst(hash);
while (e != null) {
if (e.hash == hash && key.equals(e.key))
return true;
e = e.next;
}
}
return false;
}Cross section operation
Some operations need to involve multiple segments, such as size(), containsValaue(). Let's look at the size () method first:
public int size() {
final Segment<K,V>[] segments = this.segments;
long sum = 0;
long check = 0;
int[] mc = new int[segments.length];
// Try a few times to get accurate count. On failure due to
// continuous async changes in table, resort to locking.
for (int k = 0; k < RETRIES_BEFORE_LOCK; ++k) {
check = 0;
sum = 0;
int mcsum = 0;
for (int i = 0; i < segments.length; ++i) {
sum += segments[i].count;
mcsum += mc[i] = segments[i].modCount;
}
if (mcsum != 0) {
for (int i = 0; i < segments.length; ++i) {
check += segments[i].count;
if (mc[i] != segments[i].modCount) {
check = -1; // force retry
break;
}
}
}
if (check == sum)
break;
}
if (check != sum) { // Resort to locking all segments
sum = 0;
for (int i = 0; i < segments.length; ++i)
segments[i].lock();
for (int i = 0; i < segments.length; ++i)
sum += segments[i].count;
for (int i = 0; i < segments.length; ++i)
segments[i].unlock();
}
if (sum > Integer.MAX_VALUE)
return Integer.MAX_VALUE;
else
return (int)sum;
}The main idea of the size method is to sum the sizes of all segments without locks. If it is not successful (this is because there may be other threads in the process of traversal that are updating the structure of the segments that have been traversed), the maximum number of retries'before'locks will be executed. If it is not successful, the sum of the sizes of all segments will be performed with all Segment locks. In the case of no lock, it mainly uses the modCount in the Segment to detect, saves the modCount of each Segment in the process of traversal, and then detects whether the modCount of each Segment has changed after traversal. If there is a change, it means that other threads are carrying out structural concurrent update of the Segment, which needs to be recalculated.
In fact, there is a problem in this way. In the first inner for loop, between the two statements sum += segments[i].count; mcsum += mc[i] = segments[i].modCount;, other threads may be making structural changes to segments, resulting in inconsistent data read by segments[i].count and segments[i].modCount. This may cause the size () method to return a size that does not exist at any time. It's strange that javadoc does not explicitly mark this point. Maybe it's because the time window is too small. We need to pay attention to the implementation of size(). We must first segment[i].count to Segment [i]. Modcount. This is because segment[i].count is an access to the volatile variable, and then Segment [i]. Modcount can get almost the latest value (what I said earlier is "almost"). This is vividly demonstrated in the containsValue method:
public boolean containsValue(Object value) {
if (value == null)
throw new NullPointerException();
// See explanation of modCount use above
final Segment<K,V>[] segments = this.segments;
int[] mc = new int[segments.length];
// Try a few times without locking
for (int k = 0; k < RETRIES_BEFORE_LOCK; ++k) {
int sum = 0;
int mcsum = 0;
for (int i = 0; i < segments.length; ++i) {
int c = segments[i].count;
mcsum += mc[i] = segments[i].modCount;
if (segments[i].containsValue(value))
return true;
}
boolean cleanSweep = true;
if (mcsum != 0) {
for (int i = 0; i < segments.length; ++i) {
int c = segments[i].count;
if (mc[i] != segments[i].modCount) {
cleanSweep = false;
break;
}
}
}
if (cleanSweep)
return false;
}
// Resort to locking all segments
for (int i = 0; i < segments.length; ++i)
segments[i].lock();
boolean found = false;
try {
for (int i = 0; i < segments.length; ++i) {
if (segments[i].containsValue(value)) {
found = true;
break;
}
}
} finally {
for (int i = 0; i < segments.length; ++i)
segments[i].unlock();
}
return found;
}Note also that the first for loop in the inner layer contains the statement int c = segments[i].count; however, C has never been used. Even so, the compiler cannot optimize this statement to remove it, because there is a read of volatile variable count, and the only purpose of this statement is to ensure that segments[i].modCount read almost the latest value. The rest of the containsValue method will not be analyzed. It is similar to the size method.
There is also an isEmpty() method in the cross segment method, which is simpler to implement than the size() method, and it will not be introduced. At last, it briefly introduces the next iteration methods, such as keySet(), values(), entrySet(), which return the corresponding iterators. All iterators are inherited from the HashIterator class and implement the main methods. Its structure is:
abstract class HashIterator{
int nextSegmentIndex;
int nextTableIndex;
HashEntry<K,V>[] currentTable;
HashEntry<K, V> nextEntry;
HashEntry<K, V> lastReturned;
}nextSegmentIndex is the index of the segment, nextTableIndex is the index of the hash chain in the corresponding segment of nextSegmentIndex, and currentTable is the table of the corresponding segment of nextSegmentIndex. When the next method is called, the advance method is mainly called.
final void advance() {
if (nextEntry != null && (nextEntry = nextEntry.next) != null)
return;
while (nextTableIndex >= 0) {
if ( (nextEntry = currentTable[nextTableIndex--]) != null)
return;
}
while (nextSegmentIndex >= 0) {
Segment<K,V> seg = segments[nextSegmentIndex--];
if (seg.count != 0) {
currentTable = seg.table;
for (int j = currentTable.length - 1; j >= 0; --j) {
if ( (nextEntry = currentTable[j]) != null) {
nextTableIndex = j - 1;
return;
}
}
}
}
}I don't want to talk about it any more. The only thing to notice is that when you jump to the next segment, you must first read the count variable of the next segment.
The main effect of this iterative approach is that no ConcurrentModificationException is thrown. Once the table of the next segment is obtained, it means that the head node of this segment is determined in the iteration process. In the iteration process, it cannot reflect the concurrent deletion and addition of this segment node. The update of the node can be reflected because the value of the node is a volatile variable.
Finally, ConcurrentHashMap is a high-performance HashMap implementation that supports high concurrency. It supports full concurrent reading and a certain degree of concurrent writing. The implementation of ConcurrentHashMap is also very delicate, making full use of the latest JMM specification, which is worth learning but not imitating.