Concept and structure of reactor
If there is a key set K= 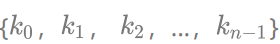
Store all its elements in a one-dimensional array in the order of a complete binary tree, and meet the following requirements: 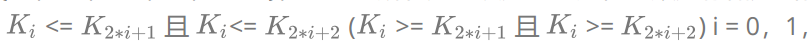
2... Is called a small pile (or a large pile). The heap with the largest root node is called the maximum heap or large root heap, and the heap with the smallest root node is called the minimum heap or small root heap.
Nature of heap:
- The value of a node in the heap is always not greater than or less than the value of its parent node;
- Heap is always a complete binary tree.

Implementation of heap
Heap down adjustment algorithm
Suppose the father's subscript is parent, the left child's subscript is equal to 2 *parent + 1, and the right child is equal to 2 *parent + 2
Now we give an array, which is logically regarded as a complete binary tree. We can adjust it through the downward adjustment algorithm starting from the root node
In a small pile or pile. The downward adjustment algorithm has a premise: the left and right subtrees must be a heap before adjustment.
Let's take adjusting the small pile as an example:
int array[] = {27,15,19,18,28,34,65,49,25,37};
- Choose the smaller 15 of the left and right children in the second layer to see who is younger between 15 and its father 27. 15 < 27, so 15 and 27 are exchanged, and then take the second layer as the root
- Because the subtree on the right is already a small heap, only look at the two child nodes 18 and 28 of 27. 18 < 28, and then compare 18 with 27. 18 < 27, so 18 and 27 exchange positions, and then take the third layer as the root
- Because the subtree of 28 is already a small pile, only look at the subtree of 27, compare the sizes of 49 and 25, 25 < 49, and then compare 25 and 27, 25 < 27, so 25 and 27 exchange positions. At this time, the whole tree is a small pile
code:
void AdjustDown(int* a, int n, int i)
{
int parent = i;
int child = parent * 2 + 1;
while (child < n)
{
if (child + 1 < n && a[child] > a[child + 1])
{
child++;
}
if (a[child] < a[parent])//Small pile
{
Swap(&a[child], &a[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
Heap creation
Next, we give an array, which can logically be regarded as a complete binary tree, but it is not a heap. Now let's calculate
Method, build it into a heap. The left and right subtrees of the root node are not heaps. How can we adjust them? Here we start with the last non leaf node
The subtree can be adjusted to the root node of the tree.
int a[] = {1,5,3,8,7,6};


Heap insertion
First insert a 10 to the end of the array, and then adjust the algorithm upward until the heap is satisfied.

Deletion of heap
Deleting the heap is to delete the data at the top of the heap, replace the last data of the data root at the top of the heap, delete the last data of the array, and then adjust the algorithm downward.

Code implementation of heap
Heap.h:
typedef int tp;
typedef struct Heap
{
tp* a;
tp capacity;
tp size;
}Heap;
// Heap construction
void HeapCreate(Heap* hp, tp* a, int n);
// Heap destruction
void HeapDestory(Heap* hp);
// Heap insertion
void HeapPush(Heap* hp,tp x);
// Deletion of heap
void HeapPop(Heap* hp);
// Take the data from the top of the heap
tp HeapTop(Heap* hp);
// Number of data in the heap
int HeapSize(Heap* hp);
// Empty judgment of heap
int HeapEmpty(Heap* hp);
//Print heap
void HeapPrint(Heap* hp);
Heap.c:
//exchange
void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
//Build pile
void AdjustDown(int* a, int n, int i)
{
int parent = i;
int child = parent * 2 + 1;
while (child < n)
{
if (child + 1 < n && a[child] > a[child + 1])
{
child++;
}
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
void AdjustUp(tp* a, tp child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
// Heap build (initialization)
void HeapCreate(Heap* hp, tp* a, int n)
{
assert(hp != NULL);
hp->a = (tp*)malloc(sizeof(tp) * n);
if (hp->a == NULL)
{
perror("malloc");
exit(-1);
}
memcpy(hp->a, a, sizeof(tp) * n);
hp->size = hp->capacity = n;
//Build a small pile
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(hp->a, n, i);
}
}
// Heap destruction
void HeapDestory(Heap* hp)
{
free(hp->a);
hp->a = NULL;
hp->size = hp->capacity = 0;
}
// Heap insertion
void HeapPush(Heap* hp, tp x)
{
assert(hp != NULL);
if (hp->size == hp->capacity)
{
tp* tmp = (tp*)realloc(hp->a, 2 * (hp->capacity) * sizeof(tp));
if (tmp == NULL)
{
perror("realloc");
tmp = NULL;
HeapDestory(&hp);
exit(-1);
}
hp->a = tmp;
hp->capacity *= 2;
}
hp->a[hp->size] = x;
hp->size++;
//It may need to be adjusted upward after insertion. Only one branch line needs to be adjusted
AdjustUp(hp->a, hp->size - 1);
}
// Delete the heap, delete the heap top data, exchange the heap top data with the last data, delete the original heap top data, and finally adjust downward
void HeapPop(Heap* hp)
{
assert(hp != NULL);
assert(!HeapEmpty(&hp));
Swap(&hp->a[0], &hp->a[hp->size - 1]);
hp->size--;
AdjustDown(hp->a, hp->size, 0);
}
// Take the data from the top of the heap
tp HeapTop(Heap* hp)
{
return hp->a[0];
}
// Number of data in the heap
int HeapSize(Heap* hp)
{
return hp->size;
}
// Empty judgment of heap
int HeapEmpty(Heap* hp)
{
return hp->size == 0;
}
void HeapPrint(Heap* hp)
{
int i = 0;
for (i = 0; i < hp->size; i++)
{
printf("%d ", hp->a[i]);
}
printf("\n\n");
int num = 0;
int levelsize = 1;
for (i = 0; i < hp->size; i++)
{
printf("%d ", hp->a[i]);
num++;
if (num == levelsize)
{
printf("\n");
num = 0;
levelsize *= 2;
}
}
printf("\n\n");
}
Application of heap
Heap sort
Heap sorting uses the idea of heap to sort. It is divided into two steps:
- Build pile
- Ascending order: build a pile
- Descending order: build small piles
- Use the idea of heap deletion to sort
Downward adjustment is used in both heap creation and heap deletion, so once you master downward adjustment, you can complete heap sorting.
TOP-K problem
TOP-K problem: that is to find the first K largest or smallest elements in data combination. Generally, the amount of data is relatively large.
For example, the top 10 professional players, the world's top 500, the rich list, the top 100 active players in the game, etc.
For the Top-K problem, the simplest and direct way you can think of is sorting. However, if the amount of data is very large, sorting is not desirable (maybe)
Data cannot be loaded into memory all at once). The best way is to use heap. The basic idea is as follows:
- Use the first K elements in the data set to build the heap
- For the first k largest elements, build a small heap
- For the first k smallest elements, build a lot
- Compare the remaining N-K elements with the heap top elements in turn. If not, replace the heap top elements
After comparing the remaining N-K elements with the top elements in turn, the remaining K elements in the heap are the first K minimum or maximum elements.
The function called by the following code is the interface implemented in the above implementation heap
void TestTopK()
{
int *a = (int*)malloc(sizeof(int)* 10000) ;
srand(time(0));
for (size_t i = 0; i < 10000; ++i)
{
a[i] = rand() % 10000;
}
a[5] = 10000 + 2;
a[32] = 10000 + 3;
a[35] = 10000 + 9;
a[19] = 10000 + 1;
a[999] = 10000 + 10;
a[25] = 10000 + 22;
a[52] = 10000 + 4;
int k = 7;
hp h;
HeapInit(&h, a, k);
HeapPrint(&h);
printf("\n");
//Put the k largest numbers in the heap
for (int j = k; j < 10000; ++j)
{
int top = HeapTop(&h);
if (a[j] > top)
{
HeapPop(&h);
HeapPush(&h, a[j]);
}
}
printf("\n");
HeapPrint(&h);
while (!HeapEmpty(&h) && k > 0)
{
printf("%d ", HeapTop(&h));
HeapPop(&h);
--k;
}
HeapDestroy(&h);
}
int main()
{
//Build a small pile
TestTopK();
return 0;
}