1. Overview
The Hannotta I have seen has two kinds of play, one is only column A->column B->column C, the other is column A->column B->column C->column A. This paper studies the Hannota game in which the tower can only move according to the rules of column A->column B->column C.
2. Step decomposition using recursion
Here's an interesting story: When a monk wanted to move the 64-story Hanoi Tower, he thought that with so many monks in the temple, I could let another monk move the 63-story Hanoi Tower above. I just moved the last 64-story Hanoi Tower. Isn't that easy? And the first monk asked to move the 63-story Hanoi Tower also thought that I could let another monk move itThe monk moved the 62-story Hanoi Tower above, and I only moved the last 63-story Hanoi Tower; the third monk thought so too. Thus, a very complex Hanoi Tower problem was broken down into a problem of moving a plate one by one, which is the idea of recursion.
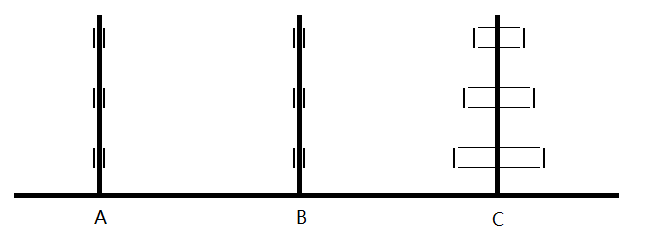
Under these rules of the game, Hannotta's problem can be broken down into five steps using recursive thinking:
(1) Transfer the n-1 Hannotta from A to C with the aid of B;
(2) Transfer layer N from A to B;
(3) Transfer the n-1 Hannotta from C to A with the help of B;
(4) Transfer layer N from B to C;
(5) Transfer the n-1 Hannotta from A to C with the help of B.
void hanoi(int n,int one,int two,int three)//n: Number of towers to move; from one to three with two.
{
void move(int x,int y);
if(n==1) //When the last layer of the current recursion needs to be moved, turn that layer in column A to B, then from B to C
{
move(one,two);
move(two,three);
}
else
{
hanoi(n-1,one,two,three);//Turn the n-1 Hannotta from A to C with the help of B, and turn the N layer from A to B.
move(one,two);
hanoi(n-1,three,two,one);//Turn the n-1 Hannotta from C to A with the help of B, and turn the N layer from B to C.
move(two,three);
hanoi(n-1,one,two,three);//Turn the n-1 Hanoi Tower from A to C with the help of B. The n-layer Hanoi Tower move task ends.
}
}Moving a plate can be accomplished using a move function:
void move(int x,int y) //Move a disk from X-column to Y-column
{
void show(int x,int y);
show(x,y);
total=total+1; //Used to record total steps
Sleep(500);
}3. Structure of data
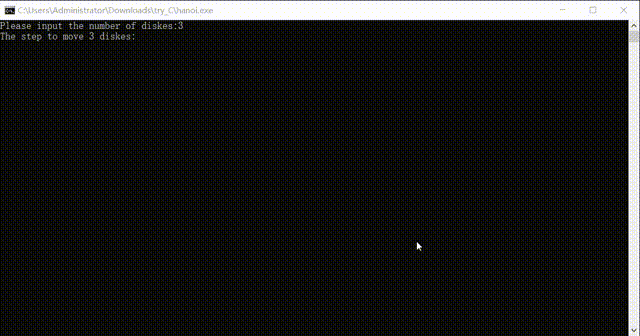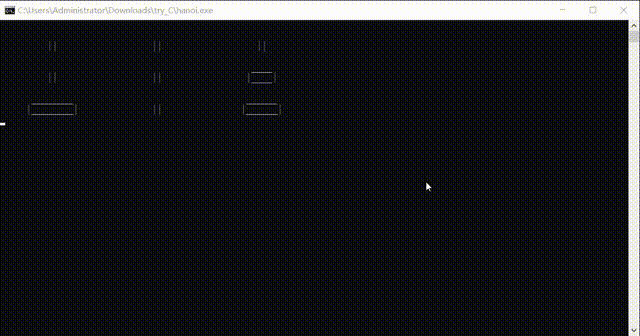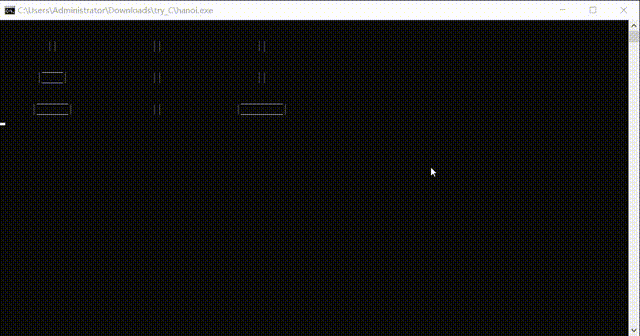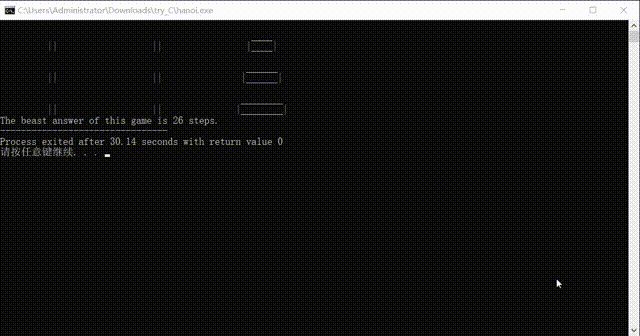
N-Layer Hannotta requires N plates. The length of the upper plate should be as long as the next layer of plate+2. This uses an array of N*3 to store the length of the plates in the three columns. In fact, using a stack here will be easier and more memory-efficient than using a fixed-size array.
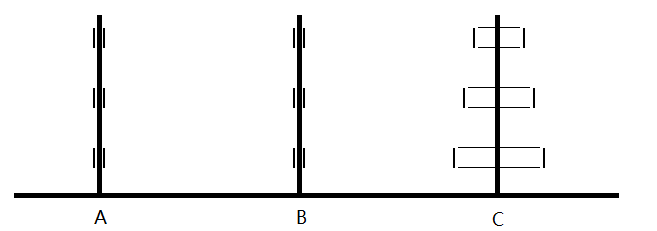
| 0 | 0 | 4 |
| 0 | 0 | 6 |
| 0 | 0 | 8 |
The table above corresponds to the storage content in the state of the diagram above.
4. Simple rectangle on command line
The author is limited in his ability to draw rectangles using spaces and English symbols'','|'on the command line:
void rectangle(int *len,int n)
{
int x;
x=5+2*(n-1); //Half the distance between columns based on the total number of layers
printf("\n");
for(int j=0;j<3;j++) //Output the top border of a row of plates (rectangles)
{
printf(" ");
for(int i=0;i<x-len[j]/2;i++)
{
printf(" ");
}
for(int i=0;i<len[j];i++)
{
printf("_");
}
for(int i=0;i<x-len[j]/2;i++)
{
printf(" ");
}
printf(" ");
}
printf("\n");
for(int j=0;j<3;j++) //Output the left, right and bottom border of a row of plates (rectangle)
{
for(int i=0;i<x-len[j]/2;i++)
{
printf(" ");
}
printf("|");
for(int i=0;i<len[j];i++)
{
printf("_");
}
printf("|");
for(int i=0;i<x-len[j]/2;i++)
{
printf(" ");
}
}
printf("\n");
}
Enclosed complete code
#include <stdio.h>
#include <stdlib.h>
#include<conio.h>
#include <Windows.h>
int total=0;
int **data;
int total_layer;
int main()
{
void hanoi(int n,int one,int two,int three);
int m;
printf("Please input the number of diskes:");
scanf("%d",&m);
total_layer=m;
data=(int**)malloc(sizeof(int*)*m);
for(int i=0;i<m;i++)
{
data[i]=(int*)malloc(sizeof(int)*3);
data[i][0]=4+2*i;
data[i][1]=0;
data[i][2]=0;
}
printf("The step to move %d diskes:\n",m);
Sleep(2*1000);
hanoi(m,1,2,3);
printf("The beast answer of this game is %d steps.",total);
for(int i=0;i<m;i++)free(data[i]);
free(data);
return 0;
}
void hanoi(int n,int one,int two,int three)
{
void move(int x,int y);
if(n==1)
{
move(one,two);
move(two,three);
}
else
{
hanoi(n-1,one,two,three);
move(one,two);
hanoi(n-1,three,two,one);
move(two,three);
hanoi(n-1,one,two,three);
}
}
void move(int x,int y)
{
void show(int x,int y);
show(x,y);
total=total+1;
Sleep(500);
}
void show(int x,int y)
{
void rectangle(int *len,int n);
static int a[3]={0,0,0};
system("cls");
if(a[0]==0 && a[1]==0 && a[2]==0)a[0]=total_layer;
int width=0;
a[x-1]=a[x-1]-1;
for(int i=0;i<total_layer;i++)
{
if(data[i][x-1]!=0)
{
width=data[i][x-1];
data[i][x-1]=0;
break;
}
}
a[y-1]=a[y-1]+1;
for(int i=0;i<total_layer;i++)
{
if(data[i][y-1]!=0)
{
data[i-1][y-1]=width;
break;
}
else if(i==total_layer-1)
{
data[i][y-1]=width;
}
}
int layer[3];
for(int i=0;i<total_layer;i++)
{
layer[0]=data[i][0];
layer[1]=data[i][1];
layer[2]=data[i][2];
rectangle(layer,total_layer);
}
}
void rectangle(int *len,int n)
{
int x;
x=5+2*(n-1);
printf("\n");
for(int j=0;j<3;j++)
{
printf(" ");
for(int i=0;i<x-len[j]/2;i++)
{
printf(" ");
}
for(int i=0;i<len[j];i++)
{
printf("_");
}
for(int i=0;i<x-len[j]/2;i++)
{
printf(" ");
}
printf(" ");
}
printf("\n");
for(int j=0;j<3;j++)
{
for(int i=0;i<x-len[j]/2;i++)
{
printf(" ");
}
printf("|");
for(int i=0;i<len[j];i++)
{
printf("_");
}
printf("|");
for(int i=0;i<x-len[j]/2;i++)
{
printf(" ");
}
}
printf("\n");
}
References
C Programming (Fifth Edition) Tan Haoqiang Tsinghua University Press