The commonly used exponential smoothing methods are first exponential smoothing, second exponential smoothing and third exponential smoothing. Higher exponential smoothing is rarely seen. Therefore, this paper focuses on the characteristics and differences of first, second and third exponential smoothing.
One-time exponential smoothing is generally applied to straight-line data, and it has lag, which can indicate that there is obvious time and seasonality.
Quadratic exponential smoothing is also generally used for straight lines, but the effect is much better than single exponential smoothing, which is equivalent to the enhanced version of single exponential smoothing.
Cubic exponential smoothing can be applied to parabolic data, since the data still has a slope after the second smoothing, cubic exponential smoothing can be continued.
Initial value: Any exponential smoothing has an initial value. If the data is greater than 20 items, the initial value can be identified as the first data, or calculated using the following formula. If the data is less than 20 items, the initial value is:
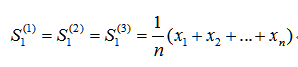
Less than 20 items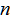
Normally take 3, more than 20 look and take.
One exponential smoothing:
One exponential smoothing requires a lag period, given the smoothing factor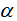
Then the formula for first exponential smoothing is:
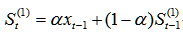
Forecast No.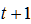
The expected value is the weighted average of the actual and predicted values of the previous period, and the prediction formula is:
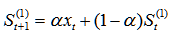
Secondary exponential smoothing:
Given smoothing factor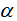Then the formula for the second exponential smoothing is:
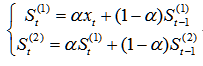
Forecast the future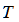
Value of period
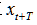The formula is:
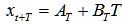
Where:
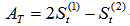
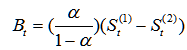
Cubic exponential smoothing:
Given smoothing factor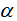Then the formula for cubic exponential smoothing is:
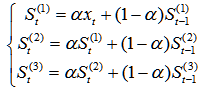
Forecast the future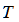Value of period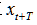The formula is:
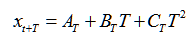
Where:
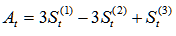
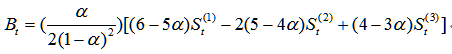
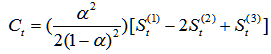
The following is an example of the data:
| 253993 |
275396.2 |
315229.5 |
356949.6 |
400158.2 |
442431.7 |
495102.9 |
570164.8 |
640993.1 |
704250.4 |
767455.4 |
781807.8 |
776332.3 |
794161.7 |
834177.7 |
931651.5 |
1028390 |
1114914 |
| 133 |
88 |
150 |
123 |
404 |
107 |
674 |
403 |
243 |
257 |
900 |
1043 |
1156 |
895 |
1200 |
1038 |
1024 |
1283 |
Introducing the concept of mean square error to judge the smoothing factor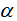Accuracy:
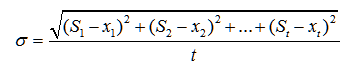
To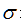
The smallest constitutes one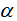about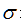Functions of
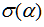Thus, an optimal smoothing factor can be obtained. Here, the idea of linear programming can be introduced to obtain an optimal solution.
But:
python doesn't have a linear programming package, so no detailed code is written, but it's possible to try this manually
Programming under python3, the exponential smoothing code at one time is:
1 S1_1 = [] 2 for m in range(0, len(info_data_id)): 3 S1_1_empty = [] 4 x = 0 5 for n in range(0, 3): 6 x = x + int(info_data_sales[m][n]) 7 x = x / 3 8 S1_1_empty.append(x) 9 S1_1.append(S1_1_empty) 10 # print(S1_1) 11 12 a = [] ##This is the array where Alpha is stored 13 info_MSE = [] ##Calculate the mean square error to get the optimal a (alpha) 14 for i in range(0, len(info_data_sales)): 15 v = input('Please enter #' + str(i + 1) + 'Group Data a: ') 16 a.append(v) 17 18 for i in range(0, len(info_data_sales)): 19 MSE = 0 20 for j in range(0, len(info_data_sales[i])): 21 S1_1[i].append( 22 float(a[i]) * int(info_data_sales[i][j]) + (1 - float(a[i])) * int(S1_1[i][j])) ##Calculate estimate 23 MSE = (int(S1_1[i][j]) - int(info_data_sales[i][j])) ** 2 + MSE 24 # print(info_data_sales[i][j], S1_1[i][j]) 25 MSE = (MSE ** (1 / 2)) / int(len(info_data_sales[i])) ##Get the mean square error 26 info_MSE.append(MSE) 27 # print(info_MSE) 28 # print(S1_1) 29 for i in range(0, len(S1_1)): 30 print('No.' + str(i + 1) + 'A smooth estimate of the group is:' + str(S1_1[i][len(S1_1[i]) - 1]) + '；The mean square error is:' + str(info_MSE[i]))
The second exponential smoothing code is:
1 S2_1 = [] 2 S2_2 = [] 3 for m in range(0, len(info_data_id)): 4 S2_1_empty = [] 5 x = 0 6 for n in range(0, 3): 7 x = x + float(info_data_sales[m][n]) 8 x = x / 3 9 S2_1_empty.append(x) 10 S2_1.append(S2_1_empty) 11 S2_2.append(S2_1_empty) 12 # print(S2_2) 13 a = [] ##This is the array where Alpha is stored 14 info_MSE = [] ##Calculate the mean square error to get the optimal a (alpha) 15 for i in range(0, len(info_data_sales)): 16 v = float(input('Please enter #' + str(i + 1) + 'Group Data a: ')) 17 a.append(v) 18 19 ##Here's how to calculate an exponentially smooth value 20 S2_1_new1 = [] 21 for i in range(0, len(info_data_sales)): 22 S2_1_new = [[]] * len(info_data_id) 23 for j in range(0, len(info_data_sales[i])): 24 if j == 0: 25 S2_1_new[i].append( 26 float(a[i]) * float(info_data_sales[i][j]) + (1 - float(a[i])) * float(S2_1[i][j])) 27 else: 28 S2_1_new[i].append(float(a[i]) * float(info_data_sales[i][j]) + (1 - float(a[i])) * float( 29 S2_1_new[i][j - 1])) ##Calculate the value of the first exponent 30 S2_1_new1.append(S2_1_new[i]) 31 # print(S2_1_new1) 32 # print(len(S2_1_new1[i])) 33 34 ##Here's how to calculate the quadratic exponential smoothing 35 S2_2_new1 = [] 36 info_MSE = [] ##Calculate the mean square error to get the optimal a (alpha) 37 for i in range(0, len(info_data_sales)): 38 S2_2_new = [[]] * len(info_data_id) 39 MSE = 0 40 for j in range(0, len(info_data_sales[i])): 41 if j == 0: 42 S2_2_new[i].append(float(a[i]) * float(S2_1_new1[i][j]) + (1 - float(a[i])) * float(S2_2[i][j])) 43 else: 44 S2_2_new[i].append(float(a[i]) * float(S2_1_new1[i][j]) + (1 - float(a[i])) * float( 45 S2_2_new[i][j - 1])) ##Calculate the value of a quadratic exponent 46 MSE = (int(S2_2_new[i][j]) - int(info_data_sales[i][j])) ** 2 + MSE 47 MSE = (MSE ** (1 / 2)) / int(len(info_data_sales[i])) 48 info_MSE.append(MSE) 49 S2_2_new1.append(S2_2_new[i]) 50 # print(S2_2_new1) 51 # print(len(S2_2_new1[i])) 52 53 ##The following are the values of At, Bt, and each estimated Xt. Calculate the estimated value directly, instead of listing the values of Xt. 54 u = input('How many periods do you want to estimate?') 55 Xt = [] 56 for i in range(0, len(info_data_sales)): 57 At = (float(S2_1_new1[i][len(S2_1_new1[i]) - 1]) * 2 - float(S2_2_new1[i][len(S2_2_new1[i]) - 1])) 58 Bt = (float(a[i]) / (1 - float(a[i])) * ( 59 float(S2_1_new1[i][len(S2_1_new1[i]) - 1]) - float(S2_2_new1[i][len(S2_2_new1[i]) - 1]))) 60 Xt.append(At + Bt * int(u)) 61 print('No.' + str(i + 1) + 'The second smoothing estimate for the group is:' + str(Xt[i]) + '；The mean square error is:' + str(info_MSE[i]))
The cubic exponential smoothing code is:
1 S3_1 = [] 2 S3_2 = [] 3 S3_3 = [] 4 for m in range(0, len(info_data_id)): 5 S3_1_empty = [] 6 x = 0 7 for n in range(0, 3): 8 x = x + float(info_data_sales[m][n]) 9 x = x / 3 10 S3_1_empty.append(x) 11 S3_1.append(S3_1_empty) 12 S3_2.append(S3_1_empty) 13 S3_3.append(S3_1_empty) 14 # print(S3_1) 15 a = [] ##This is the array where Alpha is stored 16 info_MSE = [] ##Calculate the mean square error to get the optimal a (alpha) 17 for i in range(0, len(info_data_sales)): 18 v = float(input('Please enter #' + str(i + 1) + 'Group Data a: ')) 19 a.append(v) 20 21 ##Here's how to calculate an exponentially smooth value 22 S3_1_new1 = [] 23 for i in range(0, len(info_data_sales)): 24 S3_1_new = [[]] * len(info_data_id) 25 for j in range(0, len(info_data_sales[i])): 26 if j == 0: 27 S3_1_new[i].append( 28 float(a[i]) * float(info_data_sales[i][j]) + (1 - float(a[i])) * float(S3_1[i][j])) 29 else: 30 S3_1_new[i].append(float(a[i]) * float(info_data_sales[i][j]) + (1 - float(a[i])) * float( 31 S3_1_new[i][j - 1])) ##Calculate the value of the first exponent 32 S3_1_new1.append(S3_1_new[i]) 33 34 ##Here's how to calculate the quadratic exponential smoothing 35 S3_2_new1 = [] 36 info_MSE = [] ##Calculate the mean square error to get the optimal a (alpha) 37 for i in range(0, len(info_data_sales)): 38 S3_2_new = [[]] * len(info_data_id) 39 for j in range(0, len(info_data_sales[i])): 40 if j == 0: 41 S3_2_new[i].append(float(a[i]) * float(S3_1_new1[i][j]) + (1 - float(a[i])) * float(S3_2[i][j])) 42 else: 43 S3_2_new[i].append(float(a[i]) * float(S3_1_new1[i][j]) + (1 - float(a[i])) * float( 44 S3_2_new[i][j - 1])) ##Calculate the value of a quadratic exponent 45 S3_2_new1.append(S3_2_new[i]) 46 47 ##Here's how to calculate the quadratic exponential smoothing 48 S3_3_new1 = [] 49 info_MSE = [] ##Calculate the mean square error to get the optimal a (alpha) 50 for i in range(0, len(info_data_sales)): 51 S3_3_new = [[]] * len(info_data_id) 52 MSE = 0 53 for j in range(0, len(info_data_sales[i])): 54 if j == 0: 55 S3_3_new[i].append(float(a[i]) * float(S3_2_new1[i][j]) + (1 - float(a[i])) * float(S3_3[i][j])) 56 else: 57 S3_3_new[i].append(float(a[i]) * float(S3_2_new1[i][j]) + (1 - float(a[i])) * float( 58 S3_3_new[i][j - 1])) ##Calculate the value of the cubic exponent 59 MSE = (int(S3_3_new[i][j]) - int(info_data_sales[i][j])) ** 2 + MSE 60 MSE = (MSE ** (1 / 2)) / int(len(info_data_sales[i])) 61 info_MSE.append(MSE) 62 S3_3_new1.append(S3_3_new[i]) 63 # print(S3_3_new1) 64 65 ##Here are the values of At, Bt, Ct, and each estimated Xt. Calculate the estimated values directly, instead of listing them individually. 66 u = input('How many periods do you want to estimate?') 67 Xt = [] 68 for i in range(0, len(info_data_sales)): 69 At = ( 70 float(S3_1_new1[i][len(S3_1_new1[i]) - 1]) * 3 - float(S3_2_new1[i][len(S3_2_new1[i]) - 1]) * 3 + float( 71 S3_3_new1[i][len(S3_3_new1[i]) - 1])) 72 Bt = ((float(a[i]) / (2 * ((1 - float(a[i])) ** 2))) * ((6 - 5 * float(a[i])) * ( 73 float(S3_1_new1[i][len(S3_1_new1[i]) - 1]) - 2 * (5 - 4 * float(a[i])) * float( 74 S3_2_new1[i][len(S3_2_new1[i]) - 1]) + (4 - 3 * float(a[i])) * float( 75 S3_3_new1[i][len(S3_3_new1[i]) - 1])))) 76 Ct = (((float(a[i])) ** 2) / (2 * ((1 - float(a[i])) ** 2))) * ( 77 float(S3_1_new1[i][len(S3_1_new1[i]) - 1]) - float(S3_2_new1[i][len(S3_2_new1[i]) - 1])*2 + float( 78 S3_3_new1[i][len(S3_3_new1[i]) - 1])) 79 Xt.append(At + Bt * int(u) + Ct * (int(u) ** 2)) 80 print('No.' + str(i + 1) + 'The cubic smooth estimate of the group is:' + str(Xt[i]) + '；The mean square error is:' + str(info_MSE[i]))
Since the notes are clearly written, there is no longer a paragraph to explain them
It is obvious that the number column is linear, so smoothing with a quadratic exponent is better
The secondary smoothing results are as follows:
Error judgment:
| Error Judgment |
Estimate |
actual value |
error |
| Sequence 1 |
1193179 |
1192201 |
0.08% |
| Sequence 2 |
1250 |
1371 |
9.68% |
This shows that the prediction is very good
Attach the complete code:
1 from openpyxl import load_workbook 2 import xlsxwriter 3 4 if __name__ == '__main__': 5 judge = input('Select how many times to use exponential smoothing: press 1 once, 2 twice, 3 times:') 6 ##Here's opening excel to store data in an array 7 wb = load_workbook(filename=r'C:\Users\Administrator\Desktop\data.xlsx') ##Read Path 8 ws = wb.get_sheet_by_name("Sheet1") ##Read a sheet table named Sheet1 9 info_data_id = [] 10 info_data_sales = [] 11 12 for row_A in range(1, 3): ## Traverse lines 1 through 2 13 id = ws.cell(row=row_A, column=1).value ## Traverse rows 1 through 2, column 1 14 info_data_id.append(id) 15 for row_num_BtoU in range(1, len(info_data_id) + 1): ## Traverse lines 1 through 2 16 row_empty = [] ##Create an empty array for temporary storage and empty each line break 17 for i in range(2, 20): ## Traverse lines 1 to 2, columns 1 to 19 18 data = ws.cell(row=row_num_BtoU, column=i).value 19 if data == None: 20 pass 21 else: 22 row_empty.append(data) ##Store cell information in 23 info_data_sales.append(row_empty) ##Row_empty presses info_data_sales after storing 1 to 19 columns each time, and row_empty is emptied 24 # print(info_data_id) 25 # print(info_data_sales) 26 if judge == '1': 27 ##############################Here's the calculation St(1)Write below as S1_t_###################################### 28 print('You selected an exponential smoothing prediction') 29 ##The initial value of a single exponential smoothing is S1_1, and S1_1 is used to store a single smoothed value for each set of data 30 S1_1 = [] 31 for m in range(0, len(info_data_id)): 32 S1_1_empty = [] 33 x = 0 34 for n in range(0, 3): 35 x = x + int(info_data_sales[m][n]) 36 x = x / 3 37 S1_1_empty.append(x) 38 S1_1.append(S1_1_empty) 39 # print(S1_1) 40 41 a = [] ##This is the array where Alpha is stored 42 info_MSE = [] ##Calculate the mean square error to get the optimal a (alpha) 43 for i in range(0, len(info_data_sales)): 44 v = input('Please enter #' + str(i + 1) + 'Group Data a: ') 45 a.append(v) 46 47 for i in range(0, len(info_data_sales)): 48 MSE = 0 49 for j in range(0, len(info_data_sales[i])): 50 S1_1[i].append( 51 float(a[i]) * int(info_data_sales[i][j]) + (1 - float(a[i])) * int(S1_1[i][j])) ##Calculate estimate 52 MSE = (int(S1_1[i][j]) - int(info_data_sales[i][j])) ** 2 + MSE 53 # print(info_data_sales[i][j], S1_1[i][j]) 54 MSE = (MSE ** (1 / 2)) / int(len(info_data_sales[i])) ##Get the mean square error 55 info_MSE.append(MSE) 56 # print(info_MSE) 57 # print(S1_1) 58 for i in range(0, len(S1_1)): 59 print('No.' + str(i + 1) + 'A smooth estimate of the group is:' + str(S1_1[i][len(S1_1[i]) - 1]) + '；The mean square error is:' + str(info_MSE[i])) 60 61 if judge == '2': 62 ##############################Here's the calculation St(2)Write below as S2_t_###################################### 63 print('You chose a quadratic exponential smoothing prediction') 64 65 ##The initial value of the second exponential smoothing is S2_1, where S2_1_new is used to store a smoothed value for each set of data 66 S2_1 = [] 67 S2_2 = [] 68 for m in range(0, len(info_data_id)): 69 S2_1_empty = [] 70 x = 0 71 for n in range(0, 3): 72 x = x + float(info_data_sales[m][n]) 73 x = x / 3 74 S2_1_empty.append(x) 75 S2_1.append(S2_1_empty) 76 S2_2.append(S2_1_empty) 77 # print(S2_2) 78 a = [] ##This is the array where Alpha is stored 79 info_MSE = [] ##Calculate the mean square error to get the optimal a (alpha) 80 for i in range(0, len(info_data_sales)): 81 v = float(input('Please enter #' + str(i + 1) + 'Group Data a: ')) 82 a.append(v) 83 84 ##Here's how to calculate an exponentially smooth value 85 S2_1_new1 = [] 86 for i in range(0, len(info_data_sales)): 87 S2_1_new = [[]] * len(info_data_id) 88 for j in range(0, len(info_data_sales[i])): 89 if j == 0: 90 S2_1_new[i].append( 91 float(a[i]) * float(info_data_sales[i][j]) + (1 - float(a[i])) * float(S2_1[i][j])) 92 else: 93 S2_1_new[i].append(float(a[i]) * float(info_data_sales[i][j]) + (1 - float(a[i])) * float( 94 S2_1_new[i][j - 1])) ##Calculate the value of the first exponent 95 S2_1_new1.append(S2_1_new[i]) 96 # print(S2_1_new1) 97 # print(len(S2_1_new1[i])) 98 99 ##Here's how to calculate the quadratic exponential smoothing 100 S2_2_new1 = [] 101 info_MSE = [] ##Calculate the mean square error to get the optimal a (alpha) 102 for i in range(0, len(info_data_sales)): 103 S2_2_new = [[]] * len(info_data_id) 104 MSE = 0 105 for j in range(0, len(info_data_sales[i])): 106 if j == 0: 107 S2_2_new[i].append(float(a[i]) * float(S2_1_new1[i][j]) + (1 - float(a[i])) * float(S2_2[i][j])) 108 else: 109 S2_2_new[i].append(float(a[i]) * float(S2_1_new1[i][j]) + (1 - float(a[i])) * float( 110 S2_2_new[i][j - 1])) ##Calculate the value of a quadratic exponent 111 MSE = (int(S2_2_new[i][j]) - int(info_data_sales[i][j])) ** 2 + MSE 112 MSE = (MSE ** (1 / 2)) / int(len(info_data_sales[i])) 113 info_MSE.append(MSE) 114 S2_2_new1.append(S2_2_new[i]) 115 # print(S2_2_new1) 116 # print(len(S2_2_new1[i])) 117 118 ##The following are the values of At, Bt, and each estimated Xt. Calculate the estimated value directly, instead of listing the values of Xt. 119 u = input('How many periods do you want to estimate?') 120 Xt = [] 121 for i in range(0, len(info_data_sales)): 122 At = (float(S2_1_new1[i][len(S2_1_new1[i]) - 1]) * 2 - float(S2_2_new1[i][len(S2_2_new1[i]) - 1])) 123 Bt = (float(a[i]) / (1 - float(a[i])) * ( 124 float(S2_1_new1[i][len(S2_1_new1[i]) - 1]) - float(S2_2_new1[i][len(S2_2_new1[i]) - 1]))) 125 Xt.append(At + Bt * int(u)) 126 print('No.' + str(i + 1) + 'The second smoothing estimate for the group is:' + str(Xt[i]) + '；The mean square error is:' + str(info_MSE[i])) 127 128 if judge == '3': 129 ##############################Here's the calculation St(3)Write below as S3_t_###################################### 130 print('You have chosen a cubic exponential smoothing prediction') 131 S3_1 = [] 132 S3_2 = [] 133 S3_3 = [] 134 for m in range(0, len(info_data_id)): 135 S3_1_empty = [] 136 x = 0 137 for n in range(0, 3): 138 x = x + float(info_data_sales[m][n]) 139 x = x / 3 140 S3_1_empty.append(x) 141 S3_1.append(S3_1_empty) 142 S3_2.append(S3_1_empty) 143 S3_3.append(S3_1_empty) 144 # print(S3_1) 145 a = [] ##This is the array where Alpha is stored 146 info_MSE = [] ##Calculate the mean square error to get the optimal a (alpha) 147 for i in range(0, len(info_data_sales)): 148 v = float(input('Please enter #' + str(i + 1) + 'Group Data a: ')) 149 a.append(v) 150 151 ##Here's how to calculate an exponentially smooth value 152 S3_1_new1 = [] 153 for i in range(0, len(info_data_sales)): 154 S3_1_new = [[]] * len(info_data_id) 155 for j in range(0, len(info_data_sales[i])): 156 if j == 0: 157 S3_1_new[i].append( 158 float(a[i]) * float(info_data_sales[i][j]) + (1 - float(a[i])) * float(S3_1[i][j])) 159 else: 160 S3_1_new[i].append(float(a[i]) * float(info_data_sales[i][j]) + (1 - float(a[i])) * float( 161 S3_1_new[i][j - 1])) ##Calculate the value of the first exponent 162 S3_1_new1.append(S3_1_new[i]) 163 164 ##Here's how to calculate the quadratic exponential smoothing 165 S3_2_new1 = [] 166 info_MSE = [] ##Calculate the mean square error to get the optimal a (alpha) 167 for i in range(0, len(info_data_sales)): 168 S3_2_new = [[]] * len(info_data_id) 169 for j in range(0, len(info_data_sales[i])): 170 if j == 0: 171 S3_2_new[i].append(float(a[i]) * float(S3_1_new1[i][j]) + (1 - float(a[i])) * float(S3_2[i][j])) 172 else: 173 S3_2_new[i].append(float(a[i]) * float(S3_1_new1[i][j]) + (1 - float(a[i])) * float( 174 S3_2_new[i][j - 1])) ##Calculate the value of a quadratic exponent 175 S3_2_new1.append(S3_2_new[i]) 176 177 ##Here's how to calculate the quadratic exponential smoothing 178 S3_3_new1 = [] 179 info_MSE = [] ##Calculate the mean square error to get the optimal a (alpha) 180 for i in range(0, len(info_data_sales)): 181 S3_3_new = [[]] * len(info_data_id) 182 MSE = 0 183 for j in range(0, len(info_data_sales[i])): 184 if j == 0: 185 S3_3_new[i].append(float(a[i]) * float(S3_2_new1[i][j]) + (1 - float(a[i])) * float(S3_3[i][j])) 186 else: 187 S3_3_new[i].append(float(a[i]) * float(S3_2_new1[i][j]) + (1 - float(a[i])) * float( 188 S3_3_new[i][j - 1])) ##Calculate the value of the cubic exponent 189 MSE = (int(S3_3_new[i][j]) - int(info_data_sales[i][j])) ** 2 + MSE 190 MSE = (MSE ** (1 / 2)) / int(len(info_data_sales[i])) 191 info_MSE.append(MSE) 192 S3_3_new1.append(S3_3_new[i]) 193 # print(S3_3_new1) 194 195 ##Here are the values of At, Bt, Ct, and each estimated Xt. Calculate the estimated values directly, instead of listing them individually. 196 u = input('How many periods do you want to estimate?') 197 Xt = [] 198 for i in range(0, len(info_data_sales)): 199 At = ( 200 float(S3_1_new1[i][len(S3_1_new1[i]) - 1]) * 3 - float(S3_2_new1[i][len(S3_2_new1[i]) - 1]) * 3 + float( 201 S3_3_new1[i][len(S3_3_new1[i]) - 1])) 202 Bt = ((float(a[i]) / (2 * ((1 - float(a[i])) ** 2))) * ((6 - 5 * float(a[i])) * ( 203 float(S3_1_new1[i][len(S3_1_new1[i]) - 1]) - 2 * (5 - 4 * float(a[i])) * float( 204 S3_2_new1[i][len(S3_2_new1[i]) - 1]) + (4 - 3 * float(a[i])) * float( 205 S3_3_new1[i][len(S3_3_new1[i]) - 1])))) 206 Ct = (((float(a[i])) ** 2) / (2 * ((1 - float(a[i])) ** 2))) * ( 207 float(S3_1_new1[i][len(S3_1_new1[i]) - 1]) - float(S3_2_new1[i][len(S3_2_new1[i]) - 1])*2 + float( 208 S3_3_new1[i][len(S3_3_new1[i]) - 1])) 209 Xt.append(At + Bt * int(u) + Ct * (int(u) ** 2)) 210 print('No.' + str(i + 1) + 'The cubic smooth estimate of the group is:' + str(Xt[i]) + '；The mean square error is:' + str(info_MSE[i]))