1. Title
Your plane to the ICPC Finals departs in a short time, and the only way to get to the airport is by bus. Unfortunately, some of the bus drivers are considering going on strike, so you do not know whether you can get to the airport on time. Your goal is to plan your journey in such a way as to maximize the probability of catching your plane. You have a detailed map of the city, which includes all the bus stations. You are at station 0 and the airport is at station 1. You also have a complete schedule of when each bus leaves its start station and arrives at its destination station. Additionally, for each bus you know the probability that it is actually going to run as scheduled, as opposed to its driver going on strike and taking the bus out of service. Assume all these events are independent. That is, the probability of a given bus running as planned does not change if you know whether any of the other buses run as planned. If you arrive before the departure time of a bus, you can transfer to that bus. But if you arrive exactly at the departure time, you will not have enough time to get on the bus. You cannot verify ahead of time whether a given bus will run as planned – you will find out only when you try to get on the bus. So if two or more buses leave a station at the same time, you can try to get on only one of them.
Topic:
Your plane to the ICPC final will take off soon, and the only way to get to the airport is by bus.Unfortunately, some bus drivers are considering a strike, so you don't know if you can get to the airport on time.Your goal is to plan your journey in a way that maximizes your chances of catching up with the plane. You have a detailed map of the city, including all bus stops.You are at station 0 and the airport is at station 1.You also have a complete schedule showing how long each bus leaves its starting point and arrives at its destination. In addition, for each bus, you know the probability that it actually starts on a timetable, so you know the probability that its drivers will strike and stop service.Suppose all these events are independent. That is, if you know whether any other bus is running on schedule, it does not change the probability that a given bus is running on schedule. If you arrive before a bus leaves, you can change to that bus.But if you arrive just at the time when the bus leaves, you don't have enough time to get on.You can't verify in advance whether a given bus will run as planned, only if you decide to get on. Therefore, if two or more buses leave a station at the same time, you can only try to take one of them.
Input sample:

Enter a description:
The first line of input contains two integers m(1 < m < 10610 ^ 6106) and n(2 < n < 10610 ^ 6106), representing the number of buses and the number of bus stops in the city.
The second line contains an integer k(1 < K < 101810 ^{18} 1018), which indicates when you must arrive at the airport.
The next m lines are descriptions of m buses.Each row contains integers a and b(0 < a, B < n, a neq= b), representing the start and destination of the car, respectively.Next, the integers s s and t(0 < s < T < k)) indicate the departure time from station a and the arrival time a t station B.The last value p(0 < p < 1, up to 10 digits after the decimal point) in each row indicates the probability that the bus will depart on schedule.
Output:
Gives you the probability of catching up with the plane on the best route.Output error does not exceed 10_610^{6}10_6
2. Analysis
Take input sample 1 (output 0.3124) as an example, and the following is its corresponding bus schedule:
| Shift | Departure station | Destination Station | Departure time | Departure probability | Arrival time |
|---|---|---|---|---|---|
| (1) | 0 | 1 | 0 | 20% | 900 |
| (2) | 0 | 2 | 100 | 100% | 500 |
| (3) | 2 | 1 | 500 | 100% | 700 |
| (4) | 2 | 1 | 501 | 10% | 701 |
| (5) | 0 | 3 | 200 | 50% | 400 |
| (6) | 3 | 1 | 500 | 10% | 800 |
| (7) | 3 | 0 | 550 | 90% | 650 |
| (8) | 0 | 1 | 700 | 10% | 900 |
Look at the table above, which lists the start and end points of several bus routes, as well as the departure and arrival times.Next to the departure time, the probability of the route's normal operation is indicated, and if it is not, 100% of the route's normal operation is indicated.
We started at station 0, assuming we had bus number (1).If it works, it goes directly to the airport (station 1) and nothing else.If this train doesn't start properly, consider the following transfer plan.
At this point, you can consider taking the (2) bus from station 0 to station 2 and then from station 2 to station 1.First, the bus (2) will certainly start normally, but the time to reach station 2 is 500. Then look at bus (3). The departure time is 500, so I can't catch the bus (3).The departure time of bus (4) is 501, which can catch up, but the probability of normal departure is only 10%.We'll keep this scheme for a moment.See if there are any other options.
Consider taking the (5) bus from station 0 to station 3. The probability of departure is 50%, and the time to reach station 3 is 400.(6) The bus starts from 3 to 1, and the departure time is 500. It can catch up in time. The departure probability is 10%. If it starts normally, it will arrive at the airport directly.If you do not start normally, you can only return to station 0 by bus (7) at station 3 and then arrive at the airport by bus (8), and the probability of these two vehicles starting normally is 90% and 10%, respectively.
From the above analysis, the following tree chart can be drawn, in which the departure station is Station 0 and its number is inside.Each rectangular node below represents each route, and each rectangle has two parts. The key pairs in the first part represent the departure and destination sites of the route bus, respectively, and the probability of normal departure.The second part shows the probability of departure failure.For example, compared to the above departure timetable, there is a 0.2 probability from station 0 to reach station 1 by bus (1), while a 0.8 probability is other.The following figure shows:
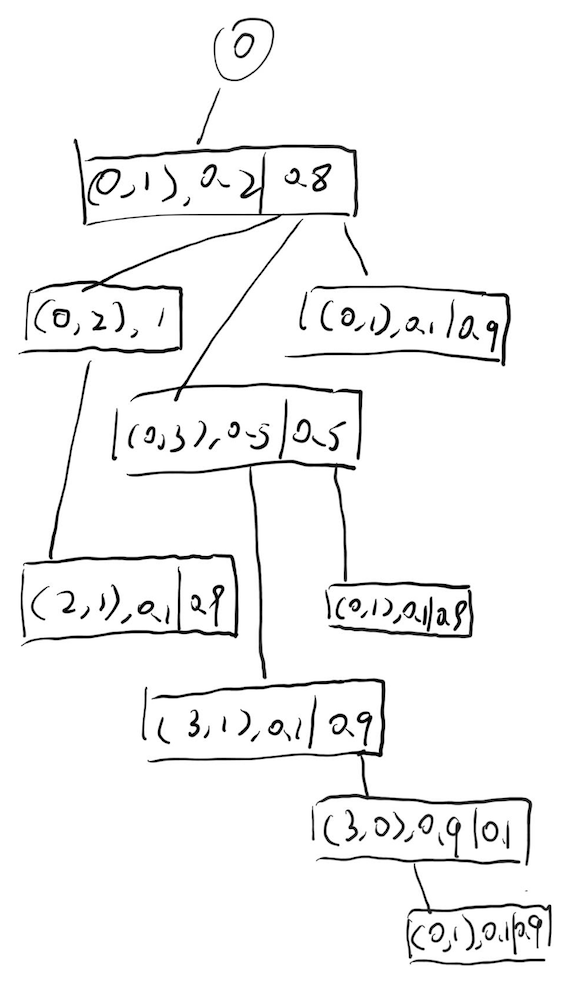
Calculate the final output from this tree:
p = max{0.2+0.8*1*(0.1), 0.2+0.8*[0.5*(0.1+0.9*0.9*0.1+0.5*0.1), 0.2+0.8*0.1] = 0.3124}
Multiply by 0 is omitted (certainly not at the airport).The probability of two parts of each rectangular node (including subnodes) needs to be added together.Considering that there can only be at most one child node on the left part of the normal departure, and that if the departure fails, there may be more than one child node on the right part of the rectangular node (representing different transfer methods), then it is necessary to split it to calculate the probability of comparing each case and ultimately to get the maximum probability.
Similarity analysis input sample 2 yields:
p = max{0.5+0.5*0.4, 0.5+0.5*0.2, 0.5+0.5*0.4, 0.5+0.5*0.2} = 0.7}
3. Python Code Implementation
from decimal import Decimal pathCount = 0 pathList = [] stationCount = 0 maxArriveTime = 0 # Node class, representing route class Node: pT = 0 # Probability of normal departure pF = 1 - pT # Probability of strikes startStation = 0 # Route departure station endStation = 0 # Route Destination Site startTime = 0 # Departure time endTime = 0 # Arrival time leftNode = None # Left Subtree rightNodes = [] # Right Subtree def __init__(self, startStation, endStation, startTime, endTime, pT): self.startStation = int(startStation) self.endStation = int(endStation) self.startTime = int(startTime) self.endTime = int(endTime) self.pT = Decimal(pT) self.pF = Decimal(1.0) - self.pT def prt(self): print(self.startStation, self.endStation, self.startTime, self.endTime, self.pT, self.pF) def printNodes(list): for node in list: node.prt() # Load input data. /input1.txt def loadInput(path): pathList = [] f = open(path) ln = 0 for line in f: if ln == 0: pathCount, stationCount = line.split() else: if ln == 1: maxArriveTime = line else: startStation, endStation, startTime, endTime, pT = line.split() node = Node(startStation, endStation, startTime, endTime, pT) pathList.append(Node(node.startStation, node.endStation, node.startTime, node.endTime, node.pT)) ln = ln + 1 f.close() return pathCount, stationCount, pathList, maxArriveTime # Find a route starting from startStation def findNodeStartAs(startStation, lastEndTime): stations = [] for node in pathList: if (node.startStation == startStation and node.startTime > lastEndTime): stations.append(node) return stations # Building a tree from a timetable def buildTree(node): if node: # Fallback finds all routes starting from the last departure and adds them all to the right subtree rightStations = findNodeStartAs(node.startStation, node.startTime) # Find all the routes starting from the current station and select the first as the left subtree leftStations = findNodeStartAs(node.endStation, node.endTime) if len(leftStations) > 0: leftNode = leftStations[0] # No matter what the probability is, the first departure car is set to leftNode if node.endStation != 1: node.leftNode = leftNode # Construct left subtree recursively buildTree(node.leftNode) # Since the departure probability is less than 1, other considerations are needed, so a right subtree is added. if node.pT < 1: node.rightNodes = rightStations # Recursively build right subtree for rnode in node.rightNodes: buildTree(rnode) # Calculate maximum probability def caculateProbability(node): if node == None: return 0 # Recursively find the maximum probability value of the right subtree, that is, the maximum probability value of the departure failure and transfer rightNodesP = [] rightP = 0; if node.rightNodes and len(node.rightNodes) > 0: for rnode in node.rightNodes: rightNodesP.append(caculateProbability(rnode)) rightP = max(rightNodesP) # Recursively find the maximum probability value of the left subtree, that is, the normal departure probability value leftP = 1; if node.leftNode: leftP = caculateProbability(node.leftNode) else: leftP = 1 # Left subtree probability plus right subtree probability return node.pT * leftP + node.pF * rightP # Step1: Read input samples pathCount, stationCount, pathList, maxArriveTime = loadInput("./input1.txt") # Step2: Construct a virtual initial node initNode = Node(0, 0, 0, -1, 1) # Step3: Execute the method to construct the tree buildTree(initNode) # Step4: Execute the method of calculating probability print("Sample 1 output:",caculateProbability(initNode))
Output after execution:
0.3124
Verify that the output of input sample 2 is 0.7, and that's OK.
THE END.