Topic link: Click Open Link

Main idea: Give you some points and find out how many convex quadrilateral can be formed.

Explanation:

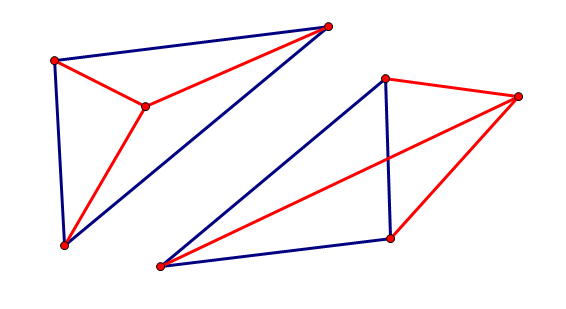
Three fixed points in a convex quadrilateral form a triangle S, and the fourth point must be outside the triangle. Therefore, if the fourth point is connected with the other three points, three triangles will be formed. If the area of the three triangles is equal to the area of the triangle S, it is not a convex quadrilateral.

The following figure:

#include <iostream>
#include <string>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <algorithm>
#include <vector>
#include <iomanip>
#include <map>
using namespace std;
typedef long long ll;

struct point{
  int x,y;
}point[50];
int area(int x1,int y1,int x2,int y2,int x3,int y3)
{
    return abs((x2-x1)*(y3-y1)-(y2-y1)*(x3-x1));
}
int solve(int i,int j,int k,int l)
{
    int Area[4];
    Area[0]=area(point[i].x,point[i].y,point[j].x,point[j].y,point[k].x,point[k].y);
    Area[1]=area(point[i].x,point[i].y,point[j].x,point[j].y,point[l].x,point[l].y);
    Area[2]=area(point[i].x,point[i].y,point[k].x,point[k].y,point[l].x,point[l].y);
    Area[3]=area(point[j].x,point[j].y,point[k].x,point[k].y,point[l].x,point[l].y);
    sort(Area,Area+4);
    if(Area[3]!=Area[0]+Area[1]+Area[2]) return 1;
    else return 0;
}

int main()
{
    int T; cin>>T;
    int kase=0;
    while(T--){
        int n; cin>>n;
        for(int i=0;i<n;i++){
            cin>>point[i].x>>point[i].y;
        }
        int num=0;
        for(int i=0;i<n;i++)
        for(int j=i+1;j<n;j++)
        for(int k=j+1;k<n;k++)
        for(int l=k+1;l<n;l++){
            if(solve(i,j,k,l))
                num++;
        }
        cout<<"Case "<<++kase<<": "<<num<<endl;


    }
    return 0;
}