hw2021 Written Test Scene 3 Question 1

_At first he was dead and alive, but he was always 0. Then he added a code, after 80%, he was going to cry...

Title Description

_There is a horizontal line with some stations and sterilizing equipment on the horizontal line. The working range of the sterilizing equipment is a circle and the working radius of all the sterilizing equipment is the same. All stations are required to be covered. Try, what is the minimum working radius?

_Input: The first line enters an array representing the position of the work station; the second line enters an array representing the position of the sterilizing device.

_Output: Minimum working radius size

_Example:

_Input:

  1 3 5

  2

_Output:

  3

_That is, the working radius is 3, and the sterilizing device position is 2, so that all positions 1, 3 and 5 can be covered.

thinking

_First of all, the station and sterilizing equipment are on the same horizontal line, and you know where they are, so you can draw a number of axes.

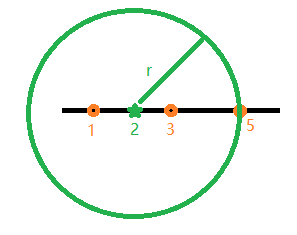
_In the case of violence, a two-layer for-loop determines if each station can be within the scope of a sterilizing device in turn, but it is easy to time out. To change the thinking, if the radius r is set to the farthest position (5)Since 5 is OK, 4 is OK,... Until r is 2 the condition is not satisfied, so the minimum working radius is 3. So it becomes the left boundary value to find the optional value of radius, that is, the minimum maximum value, so it can be found by dichotomy (you can see this). Bisection Code Analysis - Finding Left Boundary ), that is, if the mid value meets the requirements, continue to look to the left. The two-part code is as follows:

void binarySearch(const vector<int>& work, const vector<int>& ster)
{
	int small = 1, mid, big = maxWorkStation;
	
	while (small <= big) {
		mid = small + (big - small) / 2;
		if (judge(work, ster, mid)) {
			big = mid - 1;
		} else {
			small = mid + 1;
		}
	}
	
	cout << small << endl; // big + 1 is also possible
}

_The key now is to determine how the radius r meets the requirements. I calculated the interval of the working range of each sterilizing device after reading in the sterilizing device location, i.e. only the values at the two ends of the interval. If the two sterilizing devices have overlapping working ranges, merge them into one large interval, for example (1, 3), (2, 4) merge them into (1, 4)(ps: If you want to merge overlapping intervals, remember to sort the input data of the second row because it has been 0%). The code for determining this is as follows:

bool judge(const vector<int>& work, const vector<int>& ster, int r)
{
    vector<vector<int>> arr; // Storage interval endpoint value

    vector<int> tmp;
    tmp.push_back(ster[0] - r > 0 ? (ster[0] - r) : 0);
    tmp.push_back(ster[0] + r);
    arr.push_back(tmp); // Save an interval before comparing
    int cnt = 0;
    for (int i = 1; i < ster.size(); i++) {
        if (ster[i] - r > arr[cnt][1]) { // Record a new interval
            tmp[0] = ster[i] - r;
            tmp[1] = ster[i] + r;
            arr.push_back(tmp);
            cnt++;
        } else { // Otherwise merge with previous interval
            arr[cnt][1] = ster[i] + r;
        }
    }

    for (int i = 0; i < work.size(); i++) { // Determine whether a position is within an interval
        bool flag = false;
        for (int j = 0; j < arr.size(); j++) {
            if (work[i] >= arr[j][0] && work[i] <= arr[j][1]) {
                flag = true;
                break;
            }
        }
        if (!flag) {
            return false;
        }
    }

    return true; //Return true only if all jobs are available
}

Code

_The general code is here, some places are verbose, but that's it.

#include <algorithm>
#include <climits>
#include <cstdio>
#include <iostream>
#include <vector>
using namespace std;

bool judge(const vector<int>& work, const vector<int>& ster, int r)
{
    vector<vector<int>> arr; // Storage interval endpoint value

    vector<int> tmp;
    tmp.push_back(ster[0] - r > 0 ? (ster[0] - r) : 0);
    tmp.push_back(ster[0] + r);
    arr.push_back(tmp); // Save an interval first for easy comparison
    int cnt = 0;
    for (int i = 1; i < ster.size(); i++) {
        if (ster[i] - r > arr[cnt][1]) { // Create a new interval to add

            tmp[0] = ster[i] - r;
            tmp[1] = ster[i] + r;
            arr.push_back(tmp);
            cnt++;
        } else { // Otherwise merge with previous interval
            arr[cnt][1] = ster[i] + r;
        }
    }

    for (int i = 0; i < work.size(); i++) { // Determine whether a position is within an interval
        bool flag = false;
        for (int j = 0; j < arr.size(); j++) {
            if (work[i] >= arr[j][0] && work[i] <= arr[j][1]) {
                flag = true;
                break;
            }
        }
        if (!flag) {
            return false;
        }
    }

    return true; //Return true only if all jobs are available
}

int main()
{
    vector<int> work, ster;
    int tmp;
    char ch;

    int small = INT_MAX, big = 1; // Minimum and maximum values used to record jobs
    while (scanf("%d", &tmp) && scanf("%c", &ch) && ch != '\n') { // Read the first row of data
        work.push_back(tmp);
        small = small < tmp ? small : tmp;
        big = big > tmp ? big : tmp;
    }
    
    work.push_back(tmp); // Do not omit this data before line breaks
    small = small < tmp ? small : tmp;
    big = big > tmp ? big : tmp;

    // While (cin >> TMP && tmp!= 0) //Local debugging with'0'as input end flag
    while (scanf("%d", &tmp) != EOF) {
        ster.push_back(tmp);
    }
    sort(ster.begin(), ster.end()); // Sort!!!

    int mid;
    while (small <= big) {
        mid = small + (big - small) / 2;
        if (judge(work, ster, mid)) {
            big = mid - 1;
        } else {
            small = mid + 1;
        }
    }

    cout << small << endl; // big + 1 is also possible

    return 0;
}