Hungarian algorithm to find the maximum match

Keywords: Python Algorithm Machine Learning

Problem background

Given a connection graph corresponding to x and y, it is required that each xi and yi can only be matched once at most, and the maximum matching times can be calculated

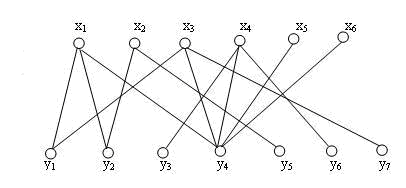
Solution idea

 ( 1) Convert the connection of x and y into a matrix, which can be connected to each other, marked as 1, and the rest as 0

y1y2y3y4y5y6y7
x11101000
x20100100
x31001001
x40011010
x50001000
x60001000

(2) The outermost loops x1 to x6, i.e. the first line to the sixth line, are traversed from y1 to y7 respectively

(3) Where used_b = [0, 0, 0, 0, 0, 0, 0] is y1 used in a row

(4)conection_b = [-1,-1,-1,-1,-1,-1,-1], where the value range of each element is 0-5, representing the row x corresponding to y

(5) Starting from the first line, y1, conection is selected_ B changes [0, - 1, - 1, - 1, - 1, - 1, - 1, - 1]

i: 0
find: 0
_index: 0
_used_b: [1, 0, 0, 0, 0, 0, 0]
_conection_b: [-1, -1, -1, -1, -1, -1, -1]
index: 0
conection_b: [0, -1, -1, -1, -1, -1, -1]
count
y1y2y3y4y5y6y7
x11101000

(6) In the second row, y2, conection is selected_ B changes [0, 1, - 1, - 1, - 1, - 1, - 1]

i: 1
find: 1
_index: 1
_used_b: [0, 1, 0, 0, 0, 0, 0]
_conection_b: [0, -1, -1, -1, -1, -1, -1]
index: 1
conection_b: [0, 1, -1, -1, -1, -1, -1]
count
y1y2y3y4y5y6y7
x11101000
x20100100

(7) In the third row, y1 is selected. Since y1 is also selected in the first row, recursion is entered

i: 2
find: 2
_index: 0
_used_b: [1, 0, 0, 0, 0, 0, 0]
_conection_b: [0, 1, -1, -1, -1, -1, -1]
find: 0
_index: 1
_used_b: [1, 1, 0, 0, 0, 0, 0]
_conection_b: [0, 1, -1, -1, -1, -1, -1]
find: 1
_index: 4
_used_b: [1, 1, 0, 0, 1, 0, 0]
_conection_b: [0, 1, -1, -1, -1, -1, -1]
index: 4
conection_b: [0, 1, -1, -1, 1, -1, -1]
index: 1
conection_b: [0, 0, -1, -1, 1, -1, -1]
index: 0
conection_b: [2, 0, -1, -1, 1, -1, -1]
count
y1y2y3y4y5y6y7
x11101000
x20100100
x31001001

(8) Get that the index of the conflicting row is 0, so start finding (0), and find that y2 is also used, so continue to recursively find(1)

y1y2y3y4y5y6y7
x11101000
x20100100
x31001001

(9) Finally x2 finds y5, so the recursion ends_ b: [2, 0, -1, -1, 1, -1, -1]

y1y2y3y4y5y6y7
x11101000
x20100100
x31001001

(10) In the fourth row, y3 is selected. Since there is no conflict, there is no conflict_ b: [2, 0, 3, -1, 1, -1, -1]

i: 3
find: 3
_index: 2
_used_b: [0, 0, 1, 0, 0, 0, 0]
_conection_b: [2, 0, -1, -1, 1, -1, -1]
index: 2
conection_b: [2, 0, 3, -1, 1, -1, -1]
count
y1y2y3y4y5y6y7
x11101000
x20100100
x31001001
x40011010

(11) In the fifth row, y4 is selected. Since there is no conflict, there is no conflict_ b: [2, 0, 3, 4, 1, -1, -1]

i: 4
find: 4
_index: 3
_used_b: [0, 0, 0, 1, 0, 0, 0]
_conection_b: [2, 0, 3, -1, 1, -1, -1]
index: 3
conection_b: [2, 0, 3, 4, 1, -1, -1]
count
y1y2y3y4y5y6y7
x11101000
x20100100
x31001001
x40011010
x50001000

(12) In the sixth row, y4 is selected. Because it conflicts with the fifth row, it enters recursive find(4)

y1y2y3y4y5y6y7
x11101000
x20100100
x31001001
x40011010
x50001000
x60001000
i: 5
find: 5
_index: 3
_used_b: [0, 0, 0, 1, 0, 0, 0]
_conection_b: [2, 0, 3, 4, 1, -1, -1]
find: 4
used_b: [0, 0, 0, 1, 0, 0, 0]
conection_b: [2, 0, 3, 4, 1, -1, -1]
5

(13) Because there are no other optional line items except y4 in the fifth row, so   find(4) = 0，conection_b has not been changed, so: conection_b: [2, 0, 3, 4, 1, -1, -1]

y1y2y3y4y5y6y7
x11101000
x20100100
x31001001
x40011010
x50001000
x60001000

code

>>>def find(x):
...    print("find:", x)
...    for index in range(7):
...        if matrix[x][index] == 1 and used_b[index] == 0:
...            used_b[index] = 1
...            print("_index:", index)
...            print("_used_b:", str(used_b))
...            print("_conection_b:", str(conection_b))
...            if conection_b[index] == -1 or find(conection_b[index]) != 0:
...                print("index:", index)
...                conection_b[index] = x
...                print("conection_b:", str(conection_b))
...                return 1
...    return 0
>>>matrix = [
...    [1,1,0,1,0,0,0],
...    [0,1,0,0,1,0,0],
...    [1,0,0,1,0,0,1],
...    [0,0,1,1,0,1,0],
...    [0,0,0,1,0,0,0],
...    [0,0,0,1,0,0,0]
...    ]
>>>conection_b = [-1 for _ in range(7)]
>>>count = 0
>>>for i in range(6):
...    used_b = [0 for _ in range(7)]
...    print("i:",i)
...    if find(i):
...        print("count")
...        count += 1
>>>print("used_b:", str(used_b))
>>>print("conection_b:", str(conection_b))
>>>print(count)
i: 0
find: 0
_index: 0
_used_b: [1, 0, 0, 0, 0, 0, 0]
_conection_b: [-1, -1, -1, -1, -1, -1, -1]
index: 0
conection_b: [0, -1, -1, -1, -1, -1, -1]
count
i: 1
find: 1
_index: 1
_used_b: [0, 1, 0, 0, 0, 0, 0]
_conection_b: [0, -1, -1, -1, -1, -1, -1]
index: 1
conection_b: [0, 1, -1, -1, -1, -1, -1]
count
i: 2
find: 2
_index: 0
_used_b: [1, 0, 0, 0, 0, 0, 0]
_conection_b: [0, 1, -1, -1, -1, -1, -1]
find: 0
_index: 1
_used_b: [1, 1, 0, 0, 0, 0, 0]
_conection_b: [0, 1, -1, -1, -1, -1, -1]
find: 1
_index: 4
_used_b: [1, 1, 0, 0, 1, 0, 0]
_conection_b: [0, 1, -1, -1, -1, -1, -1]
index: 4
conection_b: [0, 1, -1, -1, 1, -1, -1]
index: 1
conection_b: [0, 0, -1, -1, 1, -1, -1]
index: 0
conection_b: [2, 0, -1, -1, 1, -1, -1]
count
i: 3
find: 3
_index: 2
_used_b: [0, 0, 1, 0, 0, 0, 0]
_conection_b: [2, 0, -1, -1, 1, -1, -1]
index: 2
conection_b: [2, 0, 3, -1, 1, -1, -1]
count
i: 4
find: 4
_index: 3
_used_b: [0, 0, 0, 1, 0, 0, 0]
_conection_b: [2, 0, 3, -1, 1, -1, -1]
index: 3
conection_b: [2, 0, 3, 4, 1, -1, -1]
count
i: 5
find: 5
_index: 3
_used_b: [0, 0, 0, 1, 0, 0, 0]
_conection_b: [2, 0, 3, 4, 1, -1, -1]
find: 4
used_b: [0, 0, 0, 1, 0, 0, 0]
conection_b: [2, 0, 3, 4, 1, -1, -1]
5

  summary

The core idea of the Hungarian algorithm is: give priority to the last row. If there is a conflict, look for the replaceable item of the conflicting row. If there is no replaceable item, discard the last row. If there is a replaceable item, use it for substitution. If there is a conflict after substitution, enter recursion. If it is found that the conflict cannot be resolved, discard the last row and the conflict can be resolved, Use this scheme.

The significance of find recursive function is to trace back whether the scheme in the previous stage can find substitutes, so that there is no conflict between the whole matching scheme.

Posted by aosmith on Sun, 05 Sep 2021 11:51:41 -0700

Hot Keywords

©2024 Programmer Group