Huffman code Description:
Huffman coding uses the use frequency of characters to encode, and adopts the coding method of variable length, so that the frequently used character coding is shorter and the infrequently used character coding is longer;
Huffman coding has two characteristics:
1. The coding shall be as short as possible, and the higher the frequency, the shorter the coding;
2. The encoding cannot be ambiguous. The encoding of one character cannot be the prefix of another character encoding.
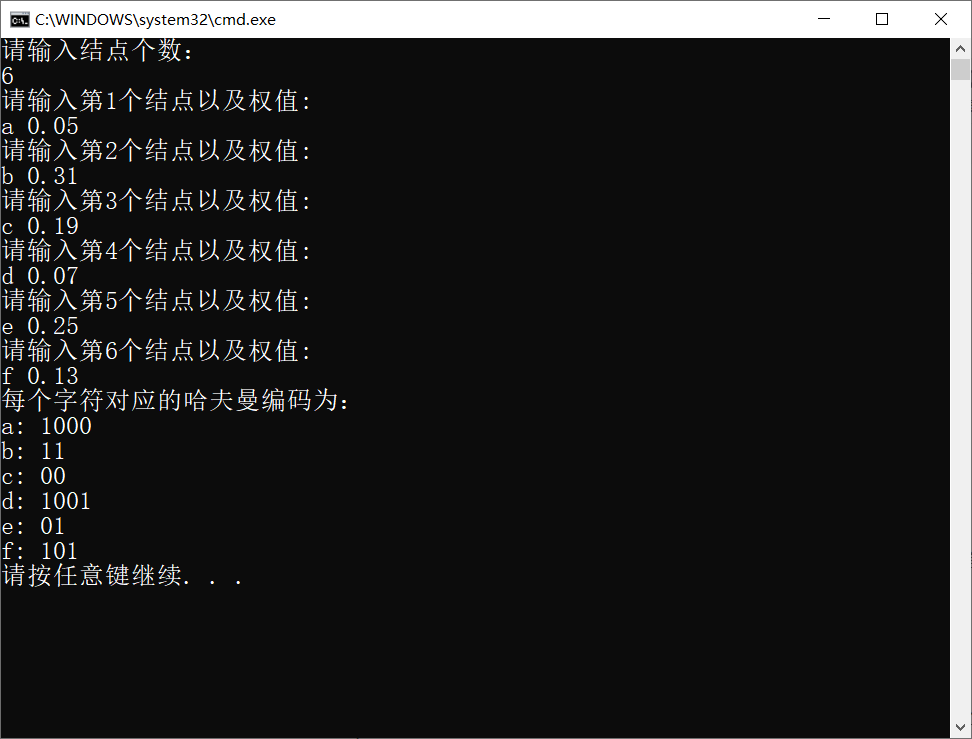
Construction of Huffman tree:
1. Firstly, the node class is defined. Each node has five members: weight (usage frequency), father, left child, right child and its own value;
class Node
{
public:
double weight; //Weight
int father;
int lchile;
int rchile;
char value; //Value of node itself
};2. Establish an array of node types. If the maximum number of characters is n, a total of 2N-1 elements need to be stored
Node huff_node[MAX_NODE * 2 - 1]; //In addition to the newly generated nodes, 2n-1 nodes need to be stored
3. Build tree:
Firstly, all 2n-1 node objects are initialized, and the father and left and right children use - 1. Then, according to the input, the weights and representative characters of the first n nodes are saved;
Then, each time, two nodes with the smallest weight are selected from the nodes without a father. The node with the smallest weight is used as the left child and the node with the second smallest weight is used as the right child to build a new tree.
The weight of the father is the sum of the weight of the left and right children. Each time a new tree is built, five members need to be changed: the father of the left and right children, the left and right children of the father, and the weight of the father; It needs to be built n-1 times (n-1 newly generated nodes).
void CreateHuffmanTree(Node* node,const int& n)
{
double m1 = 0, m2 = 0; //It is used to store the minimum weight and sub small weight
int x1 = 0, x2 = 0;
for (int i = 0; i < 2 * n - 1; i++)
{
node[i].weight = 0;
node[i].father = -1;
node[i].lchile = -1;
node[i].rchile = -1;
}
for (int i = 0; i < n; i++)
{
cout << "Please enter page" << i + 1 << "Nodes and weights:" << endl;
cin >> node[i].value >> node[i].weight;
}
for (int i = 0; i < n - 1; i++) //To build the remaining n-1 nodes
{
m1 = m2 = 0x7fffffff;
x1 = x2 = -1;
for (int j = 0; j < i + n; j++) //Find out the two orphan nodes with the smallest weight among the i+n nodes that have been constructed
{
if (node[j].weight < m1 && node[j].father == -1)
{
m2 = m1;
x2 = x1;
m1 = node[j].weight;
x1 = j;
}
else if (node[j].weight < m2 && node[j].father == -1)
{
m2 = node[j].weight;
x2 = j;
}
}
node[x1].father = n + i;
node[x2].father = n + i;
node[n + i].lchile = x1;
node[n + i].rchile = x2;
node[n + i].weight = m1 + m2;
}
}Get character Huffman code according to Huffman tree:
1. Create encoding class: an array type member used to store Huffman encoding of a character; An integer variable used to record the position where the reading starts; In Huffman tree, the nodes to be encoded are leaves, which is suitable for bottom-up. The array inserts elements from the tail.
class Code
{
public:
int code[MAX_NODE]; //Huffman coding of storage nodes
int start; //Subscript of start read
};2. Establish an encoding type array. If the maximum number of input characters is N, there are N elements in total
Code huff_code[MAX_NODE];
3. Get Huffman code
Two variables c and f are defined. c is the subscript of the node to be coded, and f is the father of c;
If C is the left node of F, insert 0 at the beginning of the corresponding character coding array, otherwise insert 1; Then move the start position of the coding array forward by 1 bit, and C and f trace back one layer upward; Repeat this process until you trace back to the root to get the code of the character c represents;
Repeat the above process n times to obtain the Huffman code of n characters
void GetHuffmanCode(Code* code, const int& n)
{
int c, f;
for (int i = 0; i < n; i++)
{
huff_code[i].start = n - 1;
c = i;
f = huff_node[c].father;
while (f != -1)
{
if (huff_node[f].lchile == c)
{
huff_code[i].code[huff_code[i].start] = 0;
}
else
{
huff_code[i].code[huff_code[i].start] = 1;
}
huff_code[i].start--;
c = f;
f = huff_node[f].father;
}
}
}
Overall code implementation:
#include <iostream>
using namespace std;
#define MAX_NODE 100
//Node class
class Node
{
public:
double weight; //Weight
int father;
int lchile;
int rchile;
char value; //Value of node itself
};
//Coding class
class Code
{
public:
int code[MAX_NODE]; //Huffman coding of storage nodes
int start; //Subscript of start read
};
Node huff_node[MAX_NODE * 2 - 1]; //In addition to the newly generated nodes, 2n-1 nodes need to be stored
Code huff_code[MAX_NODE];
//Constructing Huffman tree
void CreateHuffmanTree(Node* node,const int& n)
{
double m1 = 0, m2 = 0; //It is used to store the minimum weight and sub small weight
int x1 = 0, x2 = 0;
for (int i = 0; i < 2 * n - 1; i++)
{
node[i].weight = 0;
node[i].father = -1;
node[i].lchile = -1;
node[i].rchile = -1;
}
for (int i = 0; i < n; i++)
{
cout << "Please enter page" << i + 1 << "Nodes and weights:" << endl;
cin >> node[i].value >> node[i].weight;
}
for (int i = 0; i < n - 1; i++) //To build the remaining n-1 nodes
{
m1 = m2 = 0x7fffffff;
x1 = x2 = -1;
for (int j = 0; j < i + n; j++) //Find out the two orphan nodes with the smallest weight among the i+n nodes that have been constructed
{
if (node[j].weight < m1 && node[j].father == -1)
{
m2 = m1;
x2 = x1;
m1 = node[j].weight;
x1 = j;
}
else if (node[j].weight < m2 && node[j].father == -1)
{
m2 = node[j].weight;
x2 = j;
}
}
node[x1].father = n + i;
node[x2].father = n + i;
node[n + i].lchile = x1;
node[n + i].rchile = x2;
node[n + i].weight = m1 + m2;
}
}
//Get Huffman code
void GetHuffmanCode(Code* code, const int& n)
{
int c, f;
for (int i = 0; i < n; i++)
{
huff_code[i].start = n - 1;
c = i;
f = huff_node[c].father;
while (f != -1)
{
if (huff_node[f].lchile == c)
{
huff_code[i].code[huff_code[i].start] = 0;
}
else
{
huff_code[i].code[huff_code[i].start] = 1;
}
huff_code[i].start--;
c = f;
f = huff_node[f].father;
}
}
}
//Output Huffman coding
void InputHuffmanCode(const int& n)
{
for (int i = 0; i < n; i++)
{
cout << huff_node[i].value << ": ";
for (int j = huff_code[i].start + 1; j < n; j++)
{
cout << huff_code[i].code[j];
}
cout << endl;
}
}
int main()
{
int n;
cout << "Please enter the number of nodes:" << endl;
cin >> n;
CreateHuffmanTree(huff_node, n);
GetHuffmanCode(huff_code, n);
InputHuffmanCode(n);
return 0;
}