Redis is a cache solution that we use a lot in our daily work. Using cache can improve the performance of blind date source code and greatly reduce the pressure on the database. However, improper use will also cause many problems. Next, let's take a look at the cache penetration problem in blind date source code development.
Cache penetration
Cache penetration means that when a user looks for a data in the blind date source code, he looks for a data that doesn't exist at all. According to the cache design process, first query the redis cache and find that there is no such data, so directly query the database and find that there is no such data, so the query result ends in failure.
When there are a large number of such requests or malicious use of nonexistent data for access attacks, a large number of requests in the blind date source code will directly access the database, resulting in database pressure and even direct paralysis.
Take a look at the solution:
1. Cache empty objects
Modify the write back cache logic of the blind date source code database. For the data that does not exist in the cache and does not exist in the database, we still cache it and set a cache expiration time.
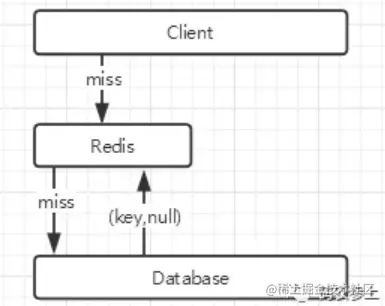
As shown in the above figure, when querying the database fails, an empty object (key, null) is still cached with the queried key value. However, there are still many problems:
a. At this time, when searching the key value in the blind date source code cache, a null empty object will be returned. It should be noted that this empty object may not be required by the client, so you need to process the result as empty and then return it to the blind source client
b. It takes up a lot of memory in redis. Because empty objects can be cached, redis will use a lot of memory to store these key s with empty values
c. If the data of this key stored in the database after writing to the cache is still null because the cache has not expired, there may be a short-term data inconsistency problem
2. Bloom filter
Bloom filter is a binary vector, or binary array, or bit array.

Because it is a binary vector, each bit of it can only store 0 or 1. When a data map needs to be added to the bloom filter, instead of the original data, multiple hash values are generated using multiple different hash functions, and the subscript position pointed to by each generated hash value is set to 1. So, don't talk about taking data from the bloom filter. We don't store the original data at all.
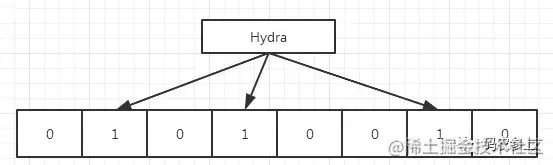
For example, if the subscripts generated by the three hash functions of "Hydra" are 1, 3 and 6 respectively, the three positions will be 1, and so on. So what effect can such a data structure have? We can judge whether the data exists according to this bit vector.
Specific process:
a. Calculating a plurality of hash values of data;
b. Judge whether these bit s are 1. If they are all 1, the data may exist;
c. If one or more bit s are not 1, it is judged that the data does not exist.
It should be noted that the bloom filter has misjudgment, because the number of bits set to 1 will increase with the increase of the data storage of the blind date source code. Therefore, it is possible that when querying a non-existent data, all bits have been set to 1 by other data, that is, hash collision occurs. Therefore, bloom filter can only judge whether the data may exist, not 100% sure.
Google's guava package provides us with a stand-alone implementation of Bloom filter. Let's take a look at the specific use
First, introduce maven dependency:
<dependency>
<groupId>com.google.guava</groupId>
<artifactId>guava</artifactId>
<version>27.1-jre</version>
</dependency>
Simulate the incoming 1000000 pieces of data into the bloom filter, give the misjudgment rate, and then use the nonexistent data for judgment:
public class BloomTest {
public static void test(int dataSize,double errorRate){
BloomFilter<Integer> bloomFilter=
BloomFilter.create(Funnels.integerFunnel(), dataSize, errorRate);
for(int i = 0; i< dataSize; i++){
bloomFilter.put(i);
}
int errorCount=0;
for(int i = dataSize; i<2* dataSize; i++){
if(bloomFilter.mightContain(i)){
errorCount++;
}
}
System.out.println("Total error count: "+errorCount);
}
public static void main(String[] args) {
BloomTest.test(1000000,0.01);
BloomTest.test(1000000,0.001);
}
}
Test results:
Total error count: 10314 Total error count: 994
It can be seen that 10314 misjudgments are made when the given misjudgment rate is 0.01 and 994 misjudgments are made when the misjudgment rate is 0.001, which is generally in line with our expectations.
However, because guava's bloom filter runs in the jvm memory, it only supports the single blind date source code and does not support the microservice distributed blind date source code. So is there a distributed bloom filter? Redis stands up and solves the problems caused by itself!
Redis's BitMap (BitMap) supports bitwise operation. A bit bit represents the corresponding value or state of an element.
//For the string value stored by key, set or clear the bit on the specified offset setbit key offset value //For the string value stored by the key, obtain the bit on the specified offset getbit key offset
Since the bloom filter assigns values to bits, we can use the setbit and getbit commands provided by BitMap to implement it very simply, and the setbit operation can realize automatic array expansion, so we don't have to worry about the lack of array bits in the process of use.
//Source code reference https://www.cnblogs.com/CodeBear/p/10911177.html
public class RedisBloomTest {
private static int dataSize = 1000;
private static double errorRate = 0.01;
//bit array length
private static long numBits;
//Number of hash functions
private static int numHashFunctions;
public static void main(String[] args) {
numBits = optimalNumOfBits(dataSize, errorRate);
numHashFunctions = optimalNumOfHashFunctions(dataSize, numBits);
System.out.println("Bits length: "+numBits);
System.out.println("Hash nums: "+numHashFunctions);
Jedis jedis = new Jedis("127.0.0.1", 6379);
for (int i = 0; i <= 1000; i++) {
long[] indexs = getIndexs(String.valueOf(i));
for (long index : indexs) {
jedis.setbit("bloom", index, true);
}
}
num:
for (int i = 1000; i < 1100; i++) {
long[] indexs = getIndexs(String.valueOf(i));
for (long index : indexs) {
Boolean isContain = jedis.getbit("bloom", index);
if (!isContain) {
System.out.println(i + "non-existent");
continue num;
}
}
System.out.println(i + "May exist");
}
}
//Get bitmap subscript according to key
private static long[] getIndexs(String key) {
long hash1 = hash(key);
long hash2 = hash1 >>> 16;
long[] result = new long[numHashFunctions];
for (int i = 0; i < numHashFunctions; i++) {
long combinedHash = hash1 + i * hash2;
if (combinedHash < 0) {
combinedHash = ~combinedHash;
}
result[i] = combinedHash % numBits;
}
return result;
}
private static long hash(String key) {
Charset charset = Charset.forName("UTF-8");
return Hashing.murmur3_128().hashObject(key, Funnels.stringFunnel(charset)).asLong();
}
//Calculate the number of hash functions
private static int optimalNumOfHashFunctions(long n, long m) {
return Math.max(1, (int) Math.round((double) m / n * Math.log(2)));
}
//Calculate bit array length
private static long optimalNumOfBits(long n, double p) {
if (p == 0) {
p = Double.MIN_VALUE;
}
return (long) (-n * Math.log(p) / (Math.log(2) * Math.log(2)));
}
}
In the process of implementing distributed bloom filter based on BitMap, the number of hash functions and the length of bit group are calculated dynamically. It can be said that the lower the given fault tolerance rate, the more the number of hash functions, the longer the array length, and the greater the redis memory overhead used by the blind date source code.
The maximum length of the bloom filter array in guava is determined by the upper limit of the int value, which is about 2.1 billion, while the bit group of redis is 512MB, that is, 2 ^ 32 bits, so the maximum length can reach 4.2 billion and the capacity is twice that of guava.
The above is the whole content of "how to solve the Redis cache penetration problem in the blind date source code?" I hope it can help you.