Title Description:

Method:
The simplest way is to find out all possible combinations and find the minimum distance from all possible combinations, but it is inefficient.
Through analysis, it is found that when a < = B < = C, their distance must be D = c-a, so it is unnecessary to calculate b-a and c-b.

1. Brute force method
2. Minimum distance method
3. Mathematical operation method

1. brute force method
Traverse the elements of the three arrays respectively, find their distances for the traversed elements, and then get the minimum distance according to the definition of distance.

Code implementation:

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
# @Time    : 2020/1/29 19:34
# @Author  : buu
# @Software: PyCharm
# @Blog    : https://blog.csdn.net/weixin_44321080
def maxx(a, b, c):
    maxs = b if b > a else a
    maxs = c if c > maxs else maxs
    return maxs


def miDistance(a, b, c):
    aLen = len(a)
    bLen = len(b)
    cLen = len(c)
    minDist = maxx(abs(a[0] - b[0]), abs(a[0] - c[0]), abs(b[0] - c[0]))
    i = 0
    while i < aLen:
        j = 0
        while j < bLen:
            k = 0
            while k < cLen:
                dist = maxx(abs(a[i] - b[j]), abs(a[i] - c[k]), abs(b[j] - c[k]))
                if dist < minDist:
                    minDist = dist
                k += 1
            j += 1
        i += 1
    return minDist


if __name__ == '__main__':
    a = [3, 4, 5, 7, 15]
    b = [10, 12, 14, 16, 17]
    c = [20, 21, 23, 24, 37, 30]
    print('min dist:', miDistance(a, b, c))

Result: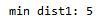

Algorithm performance analysis:

The time complexity is O(lmn);
This method does not use the character of array ascending.

2. Minimum distance method
Suppose that the elements currently traversed to these three arrays are ai, bi, ci, and ai < = bi < = ci. At this time, their distance must be Di = ci - ai. Then, the following three cases are discussed:
(1) Next, if we find the distance of ai, bi, ci+1, because ci+1 > = Ci, the distance of their triples must be Di+1 = ci+1 - ai. Obviously, Di+1 > = Di, so Di+1 cannot be the minimum distance.
(2) Next, if we find the distance of ai, bi+1, ci +, because Bi < = bi+1,

• If Bi + 1 < = Ci, the distance between them is still Di = ci - ai;
• If Bi + 1 > Ci, the distance of their triples must be Di+1 = bi+1 - ai. Obviously, Di+1 > = Di, so Di+1 cannot be the minimum distance.

(3) If we find the distance of ai+1, bi, ci next, if Di = | ci - AI | < ci - ai+1, then their distance is max (ci - ai+1, ci - bi), obviously Di+1 < Di, so Di+1 may be the minimum distance.

To sum up, only the third case needs to be considered when calculating the minimum distance. Specific implementation ideas:
Starting from the first element of the three arrays, first find out their distance minDist, then find out the array where the most decimal of the three numbers lies, only move the subscript of the array backward one position, then find the distance of the current traversal element in the three arrays, if it is smaller than minDist, then assign the current distance to minDist, and so on, until traversing one of them Array.

Code implementation:

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
# @Time    : 2020/1/29 19:49
# @Author  : buu
# @Software: PyCharm
# @Blog    : https://blog.csdn.net/weixin_44321080
def maxx(a, b, c):
    maxs = b if b > a else a
    maxs = c if c > maxs else maxs
    return maxs


def minn(a, b, c):
    mins = a if a < b else b
    mins = c if c < mins else mins
    return mins


def minDistance(a, b, c):
    aLen = len(a)
    bLen = len(b)
    cLen = len(c)
    minDist = 2 ** 32
    minElem = 0
    i, j, k = 0, 0, 0
    while True:
        curDist = maxx(abs(a[i] - b[j]), abs(a[i] - c[k]), abs(b[j] - c[k]))
        if curDist < minDist:
            minDist = curDist
        minElem = minn(a[i], b[j], c[k])
        if minElem == a[i]:
            i += 1
            if i >= aLen:
                break
        elif minElem == b[j]:
            j += 1
            if j >= bLen:
                break
        else:
            k += 1
            if k >= cLen:
                break
    return minDist


if __name__ == '__main__':
    a = [3, 4, 5, 7, 15]
    b = [10, 12, 14, 16, 17]
    c = [20, 21, 23, 24, 37, 30]
    print('min dist2:', minDistance(a, b, c))

Result: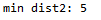

Algorithm performance analysis:
This method only needs to traverse three arrays at most, so the time complexity is O(l+m+n);

end