Recently, in the great God communication of quantitative trading, the author received such a demand that the stock code needs to be quickly converted into shaping variables, that is, the newly received stock trading information needs to be quickly combined with historical stock information, so as to make rapid decisions through trading strategies.

Since the quantitative trading speed is the lifeline, it is too slow to query the historical data of the same stock in the database directly through the stock code. At present, the common method is to directly map the stock code into a shape, and the shape after mapping is the memory address of historical data, which is a more effective method. As shown below:

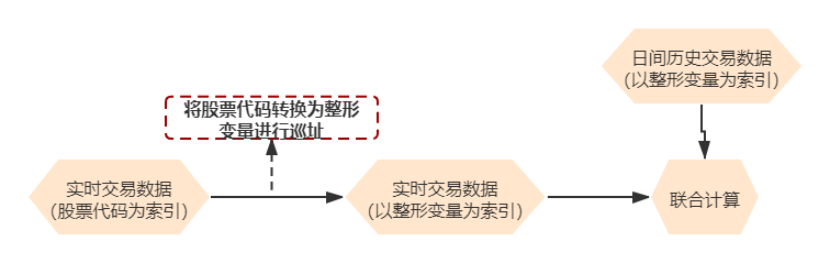
Since quantitative transactions are generally armed to the teeth, resources are basically not a problem. In short, they must be fast.

Solution analysis

Generally speaking, the current practice is to use high-speed hash algorithms such as xxhash for this conversion, but the time complexity of xxhash is still a little high for quantization scenarios. Before proposing the optimization scheme, we will analyze this requirement:

1. the first mock exam is the number of stock codes that need to be converted to twenty thousand. The total number of Listed Companies in China, the United States, Hong Kong and Europe is around tens of thousands of orders, but different markets usually use different quantitative models. The stock codes that the same model can track, and the number of trading goods such as the same period of goods and options will not exceed 10000, and the highest will not exceed 20 thousand.

2. Most stock codes are composed of 4 digits, and some long codes such as io2111-c-4900.

Solution design ideas

At present, the biggest feature of high-speed hash algorithm such as xxhash is stability. No matter how long the string is, it can be converted into an int value in a stable time. However, xxhash does not make full use of some advantageous schemes in modern computer architecture such as cache. In fact, the scheme of converting string into shaping is similar to the memory management strategy of modern operating system. Therefore, I plan to learn from the memory mapping scheme. Design a higher speed scheme from the following aspects.

1. Make full use of cache: we know that the current mainstream operating systems manage memory address mapping hierarchically and accelerate it through MMU. Moreover, considering that the upper limit of the number of stock codes we need to convert is about 20000, we also need to consider using the first 1 to 2 bits of the stock code to establish the superior index, and try to compress the size of the index so that it can be loaded into the L1 first level cache.

2. Try to avoid judging branches. I explained this in the previous why modern programming languages hate if else structure so much. Branch prediction is often an important culprit for performance degradation.

Solution and code

1. Save all stock code strings into an array and sort them. The array subscript is the int to be converted

2. Index the first two digits of the code and record the start and end serial numbers in the overall sorting array. For example, the first two digits sz of szjc are indexes. Record the start and end serial numbers of all stock codes beginning with sz through map. According to the situation of A-share market, there are about 300 data in this index. Considering that each member is composed of a two digit string (2byte) and an integer (4byte), a total of 6byte, Then 6*350=2.2k, the space complexity of map storage is generally 3 times redundant, and 2.2*3=6.6k. This size can basically enter the L1 first level cache.

3 when searching, copy the array members at the corresponding start and end positions into a new array through the first two indexes. Generally, the members of this sub array will not exceed 1000, with an average of 5 characters each. Then it should be relatively simple to transfer the space of about 5k into the first level L1 cache. Next, use the binary search to confirm the sequence number, and the corresponding int value will be obtained.

package main

import (
	"fmt"
	"math/rand"
	"sort"
	"strings"
	"time"
)

func binFind(data []string, item string) int {
	if len(data) == 0 {
		return -1
	}

	i, j := 0, len(data)-1 //Double pointer. Note that the value of j is the end subscript, not the length
	for {
		mid := (i + j) / 2 //Rounding down is required here, and Go is the default. Other languages need attention
		result := strings.Compare(item, data[mid])
		if result == 0 {
			return mid
		}
		if result < 0 {
			j = mid - 1 //Pay attention to the boundary value
		} else {
			i = mid + 1 // Pay attention to the boundary value
		}
		if i > j { //i and j cannot be used
			break
		}
	}
	return -1
}

func main() {

	var length int = 20000
	codeGen := "abcdefghijklmnopgrstuvwxyz1234567890"
	codeGroup := make([]string, length, length)
	codeOrderedGroup := make([]string, length, length)
	codeIndex := make(map[string]int)
	for j := 0; j < length; j++ {
		code := ""
		randomLen := rand.Intn(8) + 2
		for i := 0; i < randomLen; i++ {
			random := rand.Intn(len(codeGen) - 1)
			code = code + codeGen[random:random+1]
		}
		codeGroup[j] = code
		codeOrderedGroup[j] = code
	}
	sort.Strings(codeOrderedGroup)
	for k, v := range codeOrderedGroup {
		prefix := v[0:2]
		index, ok := codeIndex[prefix]
		if ok {
			codeIndex[prefix] = index&0xFFFF0000 + k
		} else {
			codeIndex[prefix] = k<<16 + k
		}
	}

	now := time.Now().UnixNano()
	//The following is how to convert strings in a random array into int shapes
	for _, v := range codeGroup {
		prefix := v[0:2]
		index := codeIndex[prefix]
		startIndex := index >> 16
		endIndex := index & 0x0000FFFF
		subcodeGroup := codeOrderedGroup[startIndex : endIndex+1]
		result := binFind(subcodeGroup, v)
		//binFind(subcodeGroup, v)
		fmt.Println(result+startIndex, v)
	}

	fmt.Println(time.Now().UnixNano() - now)
}

Of course, there is room for further optimization. For example, most of the stock codes received in real-time trading data are similar in alphabetical order. Therefore, the generation and binary search of this sub array may also be optimized in a more greedy way.

Moreover, on the high-end CPU, you can also consider using two variables to record the start and end indexes of the subarray, avoiding the current shift calculation method, which will be more efficient.