I'm trying to create a fast 2D point inside the polygon algorithm for hit testing (for example, Polygon.contains(p:Point)). Suggestions for effective technology will be appreciated.

#1 building

The C version of nirg's answer is here: I only share the code. This can save some time.

public static bool IsPointInPolygon(IList<Point> polygon, Point testPoint) {
            bool result = false;
            int j = polygon.Count() - 1;
            for (int i = 0; i < polygon.Count(); i++) {
                if (polygon[i].Y < testPoint.Y && polygon[j].Y >= testPoint.Y || polygon[j].Y < testPoint.Y && polygon[i].Y >= testPoint.Y) {
                    if (polygon[i].X + (testPoint.Y - polygon[i].Y) / (polygon[j].Y - polygon[i].Y) * (polygon[j].X - polygon[i].X) < testPoint.X) {
                        result = !result;
                    }
                }
                j = i;
            }
            return result;
        }

#2 building

Obj-C version of the nirg answer with sample methods for test points. Nirg's answer worked well for me.

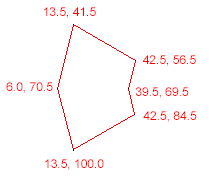
- (BOOL)isPointInPolygon:(NSArray *)vertices point:(CGPoint)test {
    NSUInteger nvert = [vertices count];
    NSInteger i, j, c = 0;
    CGPoint verti, vertj;

    for (i = 0, j = nvert-1; i < nvert; j = i++) {
        verti = [(NSValue *)[vertices objectAtIndex:i] CGPointValue];
        vertj = [(NSValue *)[vertices objectAtIndex:j] CGPointValue];
        if (( (verti.y > test.y) != (vertj.y > test.y) ) &&
        ( test.x < ( vertj.x - verti.x ) * ( test.y - verti.y ) / ( vertj.y - verti.y ) + verti.x) )
            c = !c;
    }

    return (c ? YES : NO);
}

- (void)testPoint {

    NSArray *polygonVertices = [NSArray arrayWithObjects:
        [NSValue valueWithCGPoint:CGPointMake(13.5, 41.5)],
        [NSValue valueWithCGPoint:CGPointMake(42.5, 56.5)],
        [NSValue valueWithCGPoint:CGPointMake(39.5, 69.5)],
        [NSValue valueWithCGPoint:CGPointMake(42.5, 84.5)],
        [NSValue valueWithCGPoint:CGPointMake(13.5, 100.0)],
        [NSValue valueWithCGPoint:CGPointMake(6.0, 70.5)],
        nil
    ];

    CGPoint tappedPoint = CGPointMake(23.0, 70.0);

    if ([self isPointInPolygon:polygonVertices point:tappedPoint]) {
        NSLog(@"YES");
    } else {
        NSLog(@"NO");
    }
}

#3 building

Nothing is more beautiful than the inductive definition of the problem. For the sake of completeness, you have a version in the preamble that might also clarify the point behind ray cast:

Be based on Http://www.ecse.rpi.edu/homepages/wrf/research/short'notes/pnpoly.html Simple algorithm simulation of

Some auxiliary predicates:

exor(A,B):- \+A,B;A,\+B.
in_range(Coordinate,CA,CB) :- exor((CA>Coordinate),(CB>Coordinate)).

inside(false).
inside(_,[_|[]]).
inside(X:Y, [X1:Y1,X2:Y2|R]) :- in_range(Y,Y1,Y2), X > ( ((X2-X1)*(Y-Y1))/(Y2-Y1) +      X1),toggle_ray, inside(X:Y, [X2:Y2|R]); inside(X:Y, [X2:Y2|R]).

get_line(_,_,[]).
get_line([XA:YA,XB:YB],[X1:Y1,X2:Y2|R]):- [XA:YA,XB:YB]=[X1:Y1,X2:Y2]; get_line([XA:YA,XB:YB],[X2:Y2|R]).

Given two points A and B (Line (A, b)), the linear equation is:

                    (YB-YA)
           Y - YA = ------- * (X - XA) 
                    (XB-YB) 

It is important to set the direction of rotation of the line to the clockwise direction of the boundary and the hole to the counterclockwise direction. We will check the point (X, Y), that is, whether the test point is on the left half plane of the line (this is a taste problem, it can also be on the right side, or the boundary direction). In this case, we must change the line), which is to project light from the point to the right (or left) and confirm the intersection with the line. We choose to cast light in a horizontal direction (again, this is a problem, similar restrictions can be made in a vertical direction), so we have:

               (XB-XA)
           X < ------- * (Y - YA) + XA
               (YB-YA) 

Now we need to know if the point is only on the left (or right) side of the segment, not the entire plane, so we just need to limit the search to the segment, but it's easy because only one point in the line within the segment can be higher than Y on the vertical axis. Since this is a more restrictive constraint, we need to check first, so we only select the rows that meet this requirement first, and then check their location. According to Jordan's curve theorem, any ray cast onto a polygon must intersect with an even number of lines. This is done. We project the ray to the right, and then switch its state every time we intersect the line. However, in our implementation, we need to check the length of the package solution that meets the given constraints and determine its internal conditions. You must do this for each line in the polygon.

is_left_half_plane(_,[],[],_).
is_left_half_plane(X:Y,[XA:YA,XB:YB], [[X1:Y1,X2:Y2]|R], Test) :- [XA:YA, XB:YB] =  [X1:Y1, X2:Y2], call(Test, X , (((XB - XA) * (Y - YA)) / (YB - YA) + XA)); 
                                                        is_left_half_plane(X:Y, [XA:YA, XB:YB], R, Test).

in_y_range_at_poly(Y,[XA:YA,XB:YB],Polygon) :- get_line([XA:YA,XB:YB],Polygon),  in_range(Y,YA,YB).
all_in_range(Coordinate,Polygon,Lines) :- aggregate(bag(Line),    in_y_range_at_poly(Coordinate,Line,Polygon), Lines).

traverses_ray(X:Y, Lines, Count) :- aggregate(bag(Line), is_left_half_plane(X:Y, Line, Lines, <), IntersectingLines), length(IntersectingLines, Count).

% This is the entry point predicate
inside_poly(X:Y,Polygon,Answer) :- all_in_range(Y,Polygon,Lines), traverses_ray(X:Y, Lines, Count), (1 is mod(Count,2)->Answer=inside;Answer=outside).

#4 building

This is nirg gives Of Answer Version C of the Answer Come from Professor RPI . Note that using the code in this RPI source requires attribution.

The border check box has been added to the top. However, as James Brown points out, the main code is almost as fast as the bounding box check itself, so if most of the points you want to check are inside the bounding box, the bounding box check actually slows down the overall operation. Therefore, you can check out the bounding box, or alternatively, if the bounding box of a polygon changes shape less frequently, you can precompute it.

public bool IsPointInPolygon( Point p, Point[] polygon )
{
    double minX = polygon[ 0 ].X;
    double maxX = polygon[ 0 ].X;
    double minY = polygon[ 0 ].Y;
    double maxY = polygon[ 0 ].Y;
    for ( int i = 1 ; i < polygon.Length ; i++ )
    {
        Point q = polygon[ i ];
        minX = Math.Min( q.X, minX );
        maxX = Math.Max( q.X, maxX );
        minY = Math.Min( q.Y, minY );
        maxY = Math.Max( q.Y, maxY );
    }

    if ( p.X < minX || p.X > maxX || p.Y < minY || p.Y > maxY )
    {
        return false;
    }

    // http://www.ecse.rpi.edu/Homepages/wrf/Research/Short_Notes/pnpoly.html
    bool inside = false;
    for ( int i = 0, j = polygon.Length - 1 ; i < polygon.Length ; j = i++ )
    {
        if ( ( polygon[ i ].Y > p.Y ) != ( polygon[ j ].Y > p.Y ) &&
             p.X < ( polygon[ j ].X - polygon[ i ].X ) * ( p.Y - polygon[ i ].Y ) / ( polygon[ j ].Y - polygon[ i ].Y ) + polygon[ i ].X )
        {
            inside = !inside;
        }
    }

    return inside;
}

#5 building

Just like the solution that Nirg published and edited by bobobo. I just made it javascript friendly and easier for me to read:

function insidePoly(poly, pointx, pointy) {
    var i, j;
    var inside = false;
    for (i = 0, j = poly.length - 1; i < poly.length; j = i++) {
        if(((poly[i].y > pointy) != (poly[j].y > pointy)) && (pointx < (poly[j].x-poly[i].x) * (pointy-poly[i].y) / (poly[j].y-poly[i].y) + poly[i].x) ) inside = !inside;
    }
    return inside;
}