This topic is a topic that links the operating system and Java collection classes, and it is worth studying. (Think point: the design of caching algorithm and the data format to be cached are stored in that data structure, which data structure can effectively achieve the role of caching.)

146 LRU Caching Mechanism

subject

Design and implement an LRU (least recently used) cache mechanism using the data structure you have mastered. It should support the following operations: getting data get and writing data put.
Get data get(key) - If the key exists in the cache, get the value of the key (always positive), otherwise return - 1.
Write data put(key, value) - If the key does not exist, write its data value. When the cache capacity reaches the upper limit, it should delete the least recently used data values before writing new data, thus leaving room for new data values.
Advancement:         
Can you do both within O(1) time complexity?

Example

LRUCache cache = new LRUCache( 2 /* Cache capacity */ );
cache.put(1, 1);
cache.put(2, 2);
cache.get(1);       // Return 1
cache.put(3, 3);    // This operation invalidates key 2
cache.get(2);       // Return - 1 (not found)
cache.put(4, 4);    // This operation invalidates key 1
cache.get(1);       // Return - 1 (not found)
cache.get(3);       // Return 3
cache.get(4);       // Return 4

Most recently unused permutation algorithm (LRU)

Choose pages that haven't been visited for the longest time and weed them out. It believes that pages that haven't been visited in the past may not be visited in the near future. The algorithm sets an access field for each page to record the time that the page has experienced since it was last visited. When the page is eliminated, the maximum median value (that is, the longest time) of the existing page is selected to be eliminated.

1.jpg

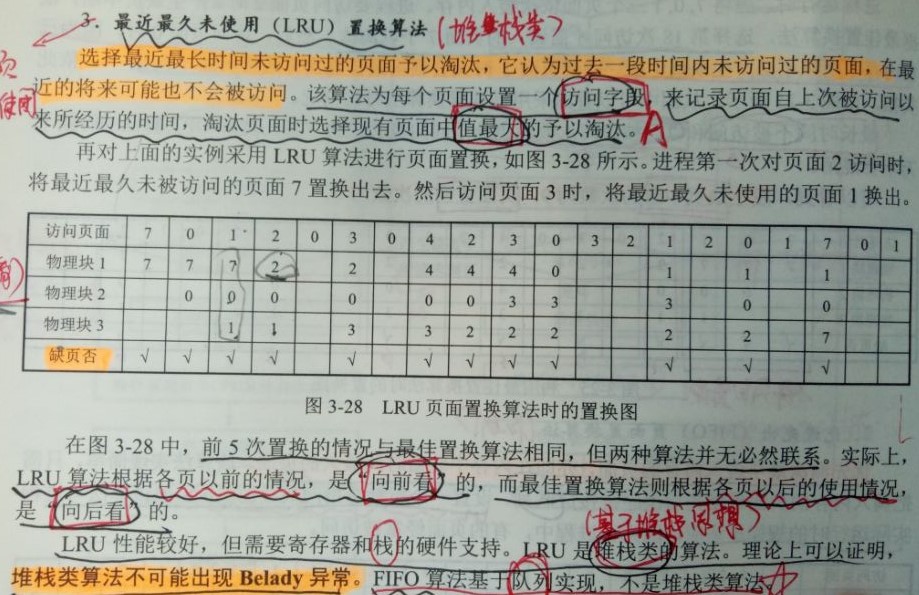
Detailed procedures can be referred to below:

image.png

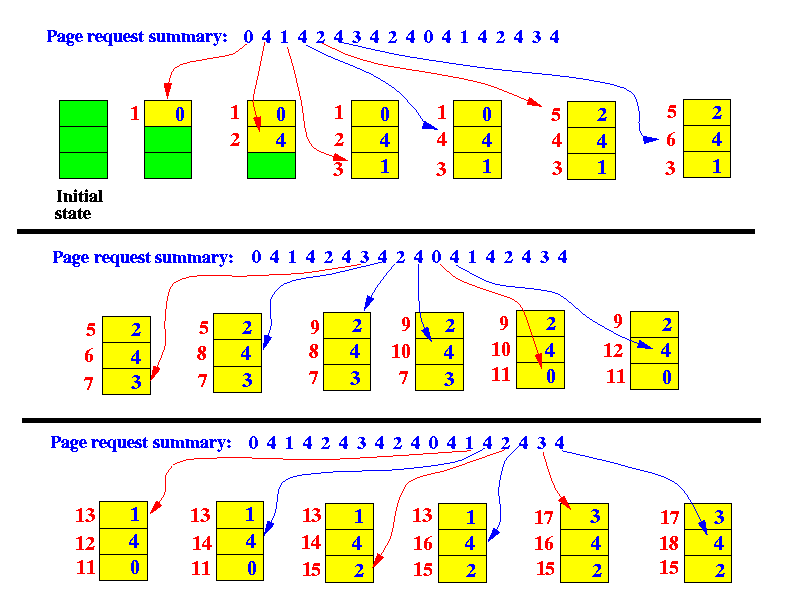
LRU Caching Mechanism

Understanding what LRU has not used permutation algorithm recently. Let's think about how to design this caching system, what kind of data structure area to store the data, and what kind of characteristics should such data structure conform to?

LRU Implementation Based on HashMap and Bidirectional Link List

Reference:[ Architects who do not understand machine learning are not good CTO s]

The overall design idea is to use HashMap to store keys, so that the time of save(key,value) and get(key) is O(1), while the Value of HashMap points to the Node node of LRU implemented by a two-way linked list, as shown in the following figure:

image.png

image.png

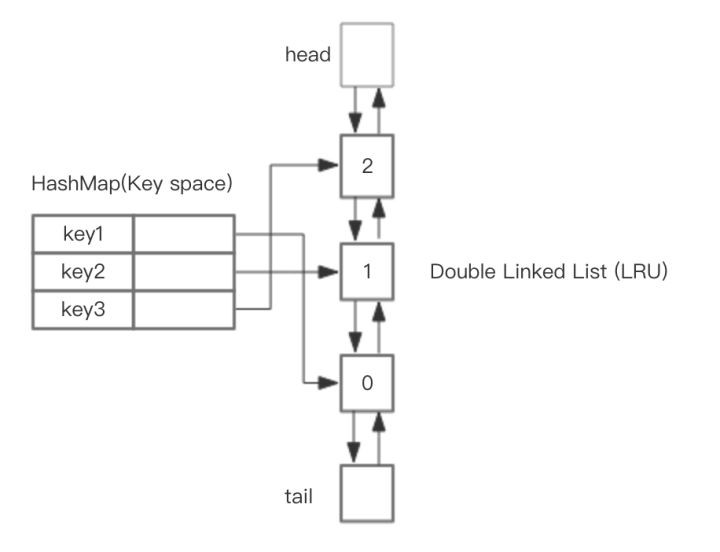
LRU storage is based on two-way linked list. The following figure demonstrates its principle. The head represents the head of the two-way linked list and the tail represents the tail. Firstly, the capacity of LRU is pre-set. If the storage is full, the tail of the bidirectional list can be eliminated by O(1) time. Every time data is added and accessed, new nodes can be added to the head through O(1) efficiency, or existing nodes can be moved to the head.

The capacity of HashMap is preset to be 3, and the changes in LRU cache during storage and access are shown below. To simplify the complexity of the graph, the changes in the HashMap section are not shown in the graph, but only the changes in the LRU bidirectional list shown in the figure above. The sequence of operations for this LRU cache is as follows:

save("key1", 7)
save("key2", 0)
save("key3", 1)
save("key4", 2)
get("key2")
save("key5", 3)
get("key2")
save("key6", 4)

The corresponding LRU bidirectional list changes as follows:

image.png

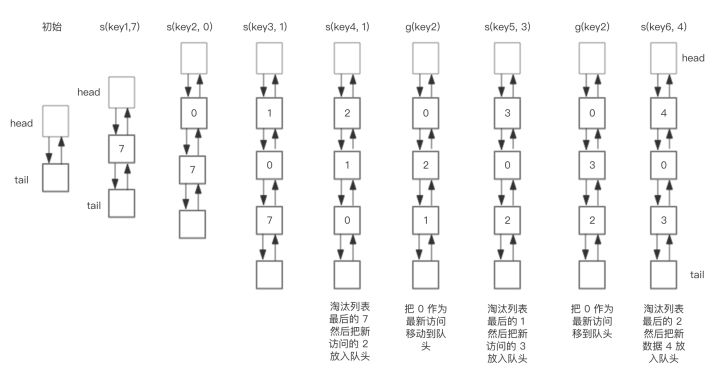
Summarize the steps of the core operation:

• 1.save(key, value), first find the Key corresponding node in HashMap, if the node exists, update the value of the node, and move the node to the head of the queue. If it does not exist, we need to construct new nodes and try to plug them into the head of the queue. If the LRU space is insufficient, we can eliminate the nodes at the end of the queue by tail and remove the Key from HashMap.

• 2.get(key), find LRU linked list node through HashMap, because according to LRU principle, this node is the latest access, so insert the node into the head of the queue, and then return the cached value.

Refer to the code in the following video: cspiration

//Initialize the nodes of the bidirectional linked list
class DLinkedNode {
    int key;
    int value;
    DLinkedNode pre;
    DLinkedNode post;
}

/**
 * Always add the new node right after head;
 */
private void addNode(DLinkedNode node){
    node.pre = head;
    node.post = head.post;
    
    head.post.pre = node;
    head.post = node;
}

/**
 * Remove an existing node from the linked list.
 */
private void removeNode(DLinkedNode node){
    DLinkedNode pre = node.pre;
    DLinkedNode post = node.post;
    
    pre.post = post;
    post.pre = pre;
}

/**
 * Move certain node in between to the head.
 */
private void moveToHead(DLinkedNode node){
    this.removeNode(node);
    this.addNode(node);
}

// pop the current tail. 
private DLinkedNode popTail(){
    DLinkedNode res = tail.pre;
    this.removeNode(res);
    return res;
}

    private Hashtable<Integer, DLinkedNode> 
    cache = new Hashtable<Integer, DLinkedNode>();
    private int count;
    private int capacity;
    private DLinkedNode head, tail;

public LRUCache(int capacity) {
    this.count = 0;
    this.capacity = capacity;

    head = new DLinkedNode();
    head.pre = null;
    
    tail = new DLinkedNode();
    tail.post = null;
    
    head.post = tail;
    tail.pre = head;
}

public int get(int key) {
    
    DLinkedNode node = cache.get(key);
    if(node == null){
        return -1; // should raise exception here.
    }
    // move the accessed node to the head;
    this.moveToHead(node);
    return node.value;
}


public void set(int key, int value) {
    DLinkedNode node = cache.get(key);
    //Determine whether the node is null
    if(node == null){
        DLinkedNode newNode = new DLinkedNode();
        newNode.key = key;
        newNode.value = value;
        this.cache.put(key, newNode);
        this.addNode(newNode);
        ++count;
        if(count > capacity){
            // pop the tail
            DLinkedNode tail = this.popTail();
            this.cache.remove(tail.key);
            --count;
        }
    }else{
        // update the value.
        node.value = value;
        this.moveToHead(node);
    }
    
}