Hough transform is a feature extraction technology in image processing. It detects objects with specific shapes (mathematical model + parameters) through a voting algorithm. In the (one) parameter space, by calculating the local maximum value of the cumulative result, a set conforming to the specific shape is obtained as the result of Hough transform.

Hough transform was first proposed by Paul Hough in 1962 [53], and then popularized by Richard Duda and Peter Hart in 1972 [54]. The classical Hough transform was used to detect the straight line in the image. Later, Hough transform was extended to the recognition of arbitrary shape objects, mostly circles and ellipses.

hough transform uses the transformation between two coordinate spaces to map a curve or line with the same shape (mathematical model + parameter) in one (image) space to a point in another (parameter) coordinate space to form a peak value, thus transforming the problem of detecting any shape into the problem of statistical peak value. (the straight-line characteristics of lane have been introduced in the previous section, and the principle and results of hough transform detection of straight-line are introduced in this section.)

We know that a straight line can be expressed b y y = k x + B in the rectangular (image) coordinate system. The main idea of Hough transform is to exchange the parameters and variables of the equation, that is, x,y as (parameters, coefficients), k,b as (variables). Therefore, a point (x1,y1) in the rectangular coordinate system is expressed as a straight line: y1=x1 · k+b, where (k,b) Is any point on the line; a line y=kx+b in the rectangular coordinate system is expressed as a point in the parameter space: (k,b). In order to facilitate the calculation and solve the problem that K (slope of the line) is close to infinity, a standard line identification method is used to express the coordinates in the parameter space as γ and θ in the polar coordinate.

The conversion of the above figure to ρ, θ space is through the conversion of K, b parameter space. Because in K, B space, the intersection point of straight lines represents the slope and intercept under the rectangular coordinate system. Only when k, B space is transferred to ρ, θ space, can the curve of θ space intersect at one point. If directly from the original rectangular coordinate system to ρ, θ space, it is obvious that the original rectangular coordinate system can be known The points under the system do not appear in the same Θ position. In fact, the transformation from the original rectangular coordinate system to the polar coordinate space has undergone two transformations. The reason for the transformation to the polar coordinate space is that K and B spaces can not solve the problem of infinite computation when k is Tan 90 degrees.

Because the parameter (k,b) / (γ) corresponding to the point on the same line, θ) It is the same, so we can first detect the edge of the image, and then transform every non-zero pixel point on the image into a straight line under the parameter coordinate, then the points belonging to the same straight line under the rectangular coordinate will form multiple straight lines in the parameter space and intersect at one point, which is the parameter of the corresponding straight line, and all the straight lines are in (γ, θ) A series of corresponding curves are obtained in parameter space. Therefore, the principle can be used for line detection.

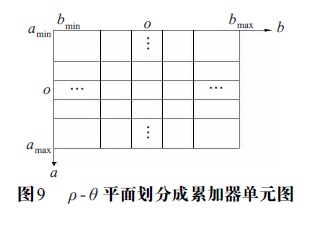
The attraction of Hough transform in calculation is to further divide the parameter space into so-called accumulator units, as shown in Figure 9. Where (amax, amin) and (bmax, bmin) are the expected ranges of parameter values. Generally speaking, the maximum ranges of values are - 90 ° < θ < 90 ° and - d < ρ < D, where D is the distance between the corners in the image. Initially, these units are set to 0. Then, for each non background point (xk, yk) on the image plane, let θ equal to the subdivision value allowed on the θ axis, and get the corresponding ρ value through the formula ρ = xkcos θ + yksin θ. And then, you get the value of ρ four Round to the nearest unit value allowed on the ρ axis, and add the corresponding accumulator units. At the end of this process, A(i,j) means that the Q points on the x-y plane lie on the line xcos θ j+ysin θ J = ρ i. The accuracy of collinearity of these points is determined by the number of subdivisions in the ρ - θ plane.

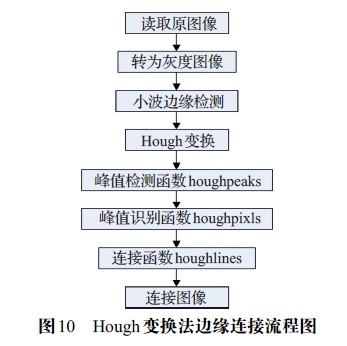
(1) Read the original image and convert it to grayscale image.
(2) Wavelet edge detection algorithm is used to detect the edge of the image and get the binary edge image.
(3) Hough transform the edge image.
(4) The houghpeaks function is used for peak detection. The algorithm of houghpeaks function is as follows:
① find the Hough transform unit with the maximum value and record its position;
(2) set the Hough transform unit in the domain of the maximum value point found in the previous step to 0;
③ repeat this step until the required number of peaks is found or a specified threshold value is reached.
(5) Once a group of candidate peak waves are identified in Hough transform, it remains to be determined whether there are line segments related to these peaks and their start and end. For each peak, the first step is to find the location of each non-zero value point in the image that affects the peak value. Therefore, the houghpixls function is written to achieve this function.
(6) The function houghlines is used to realize line edge connection. The algorithm of the function houghlines is as follows:
(1) rotate the pixel positions 90 ° - θ so that they are approximately on a vertical line;
(2) rank the pixel positions according to the x value of rotation;
③ use the function diff to find the crack. Ignore small cracks, which will merge adjacent lines separated by small blanks;
④ return the information of the line segment longer than the minimum threshold.

Opencv version

1. void CCVMFCView::OnHoughLines()  
2. {  
3.     IplImage* src = 0,*color_dst;  
4.     CvMemStorage* storage = cvCreateMemStorage(0);  
5.     CvSeq* lines = 0;  
6.     int i;  
7.   
8.     if (workImg->nChannels==3) {  
9.         src = cvCreateImage(cvGetSize(workImg), IPL_DEPTH_8U, 1);  
10.         cvCvtColor(workImg, src, CV_BGR2GRAY);  
11.     }  
12.     else {  
13.         src = cvCloneImage( workImg );  
14.     }  
15.   
16.     dst = cvCreateImage( cvGetSize(src), 8 ,1 );  
17.     color_dst = cvCreateImage( cvGetSize(src), 8 ,3);  
18.     cvFlip(src);  
19.     cvCanny( src, dst, 50, 120, 3 );  
20.     cvCvtColor(dst,color_dst,CV_GRAY2BGR);  
21.   
22.     lines = cvHoughLines2( dst, storage, CV_HOUGH_PROBABILISTIC, 1, CV_PI/180, 20, 20,30 );  
23.     //lines = cvHoughLines2( dst, storage, CV_HOUGH_PROBABILISTIC, 1,CV_PI/180, 80, 60,30 );  
24.   
25.     for( i = 0; i < lines->total; i++ )  
26.     {  
27.         CvPoint* line = (CvPoint*)cvGetSeqElem(lines,i);  
28.         cvLine( color_dst, line[0], line[1], CV_RGB(255,0,0), 3, CV_AA, 0 );  
29.     }  
30.   
31.     cvNamedWindow( "Hough", 1 );  
32.     cvShowImage( "Hough", color_dst );  
33.   
34.     cvWaitKey(0);  
35.   
36.     cvReleaseMemStorage(&storage );  
37.     cvReleaseImage( &src );  
38.     cvReleaseImage( &dst );  
39.     cvDestroyWindow( "Hough" );  
40. }