1. The first problem of HMM: A known HMM model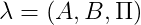That is, the state transition matrix, the emission matrix, the initial state probability matrix are known, and a sequence of observed values is given.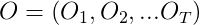To calculate the probability of occurrence of this observation sequence.

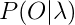2. Algorithmic thinking: Actually, it is a dynamic programming algorithm. The key is to find recursive formulas.

2.1 Calculate the forward probabilities of various states at time 1:,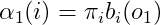 

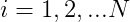
2.2 The probability of recursive 2,3...T time: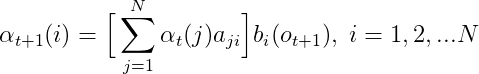

2.3 Calculate the final result: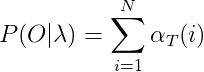

 

3.c++ code:

// Known: HMM implied state number, state transition probability, state emission probability, and initial state probability distribution, according to the specified visible state chain,
// Seek: The probability of the occurrence of this state chain
// Using forward algorithm to solve time complexity will reduce a lot.
// Following is the C++ version forward algorithm process
#include <iostream>
using namespace std;

void forward(double TransProbMatrix[][3], int irow, int icol,
			 double EmitProbMatrix[][2], int jrow, int jcol,
			 double PI[], int piLength,
			 int ObservedChain[], int obLength)
{
    // The result matrix is constructed, and each column represents the operation result of each step and state.
	const int row = piLength;
	const int col = obLength;
	double** resultMatrix = new double*[row];
	for (int i = 0; i < row; i++)
		resultMatrix[i] = new double [col];
	for (int i = 0; i < row; i++){
		for (int j = 0; j <col; j++)
			resultMatrix[i][j] = 0;
	}

	// The first step is initialization, and the next step is obtained by recursive formula.
	for (int i = 0; i < col; i++){
		if (i == 0){
			for (int j = 0; j < row; j++){
				resultMatrix[j][0] = PI[j]*EmitProbMatrix[j][0];
			}
		}
		else{
			for (int j = 0; j < row; j++){
				for (int k = 0; k < row; k++){
				    resultMatrix[j][i] += resultMatrix[k][i-1] * TransProbMatrix[k][j] * EmitProbMatrix[j][ObservedChain[i]];
				}
			}
		}
	}
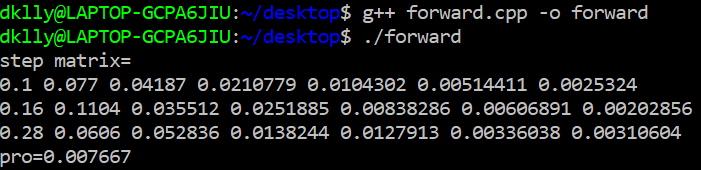
	cout<<"step matrix="<<endl;
	// Display result matrix
	double pro = 0;
	for (int i = 0; i < row; i++){
		for (int j = 0; j <col; j++){
			cout<<resultMatrix[i][j]<<" ";
			if (j == col-1)
			    pro += resultMatrix[i][j];
		}
		cout<<endl;
	}
	cout<<"pro="<<pro<<endl;
}
int main()
{
	// State transition matrix
	double TransProbMatrix[][3] =
	{{0.5,0.2,0.3},
	{0.3,0.5,0.2},
	{0.2,0.3,0.5}};
	int tRow = sizeof(TransProbMatrix)/sizeof(*TransProbMatrix);
	int tCol = sizeof(*TransProbMatrix)/sizeof(**TransProbMatrix);
	// Emission matrix
	double EmitProbMatrix[][2] = 
	{{0.5,0.5},
	{0.4,0.6},
	{0.7,0.3}};
	int eRow = sizeof(EmitProbMatrix)/sizeof(*EmitProbMatrix);
	int eCol = sizeof(*EmitProbMatrix)/sizeof(**EmitProbMatrix);
	// Initial State Probability Distribution
	double PI[] = {0.2, 0.4, 0.4};
	int piLen = sizeof(PI)/sizeof(*PI);
	// Observation chain
	int ObservedChain[] = {0, 1, 0, 1, 0, 1, 0};
	int obLen = sizeof(ObservedChain)/sizeof(*ObservedChain);
	// Afferent parameter
	forward(TransProbMatrix, 3, 3, EmitProbMatrix, 3, 2, PI, 3, ObservedChain, obLen);
}

The result is: