Heap (priority queue)

Time complexity:

The time complexity of initializing heap building is O(n)

Heap sort rebuild heap O(nlogn)

PriorityQueue small top heap

Small top heap: the weight of any non leaf node is not greater than the weight of its left and right child nodes

Constructor

constructor	Function introduction
PriorityQueue()	Create an empty priority queue with a default capacity of 11
PriorityQueue(int initialCapacity)	Create a priority queue with an initial capacity of initialCapacity. Note: initialCapacity cannot be less than 1, otherwise an IllegalArgumentException exception will be thrown
PriorityQueue(Collection c)	Use a collection to create priority queues

You can also specify the implementation of the comparator interface during initialization,

Common APIs

Function name	Function introduction
boolean offer(E e)	Insert element E and return true after successful insertion. If the e object is empty, a NullPointerException exception will be thrown, which reduces the time complexity O ( l o g 2 N ) O(log_2N) O(log2 # N), note: capacity expansion will be carried out when there is not enough space
E peek()	Gets the element with the highest priority. If the priority queue is empty, null is returned
E poll()	Remove the element with the highest priority and return it. If the priority queue is empty, return null
int size()	Get the number of valid elements
void clear()	Empty boolean
isEmpty()	Check whether the priority queue is empty, and return true if it is empty

characteristic:

1. PriorityQueue is thread unsafe, and PriorityBlockingQueue is thread safe

2. The objects stored in PriorityQueue must be able to compare sizes. If the sizes cannot be compared, ClassCaseException will be thrown

3. Cannot insert null object, otherwise NullPointerException will be thrown

4. With automatic capacity expansion mechanism

5. The time complexity of inserting and killing is
   O ( l o g 2 N ) O(log_2N) O(log2​N)

6. The bottom layer uses a heap

Capacity expansion process jdk1.8

    private void grow(int minCapacity) {
        int oldCapacity = queue.length;
        // Double size if small; else grow by 50%
        int newCapacity = oldCapacity + ((oldCapacity < 64) ?
                                         (oldCapacity + 2) :
                                         (oldCapacity >> 1));
        // overflow-conscious code
        if (newCapacity - MAX_ARRAY_SIZE > 0)
            newCapacity = hugeCapacity(minCapacity);
        queue = Arrays.copyOf(queue, newCapacity);
    }

It can be seen from the expansion method

• If the capacity is less than 64, use oldCapacity+oldCapacity+2
• If the capacity is greater than 64, use oldcapacity + (oldcapacity > > 1) (equivalent to 1.5 times capacity expansion)

Underlying data structure

Concept of heap

A key set k={k,k1,k2,k3... kn-1} is stored in the array in the order of a complete binary tree

In a one-dimensional array

• Those satisfying ki < = k2i + 1 and Ki < = k2i + 2 are called small heaps
• Those that satisfy ki > = k2i + 1 and Ki > = k2i + 2 are called piles

The heap with the largest root node is called the maximum heap or large root heap, and the heap with the smallest root node is called the minimum heap or small root heap.

nature:

• The value of a node in the heap is always not greater than or less than the value of the parent node
• Heap is always a complete binary tree

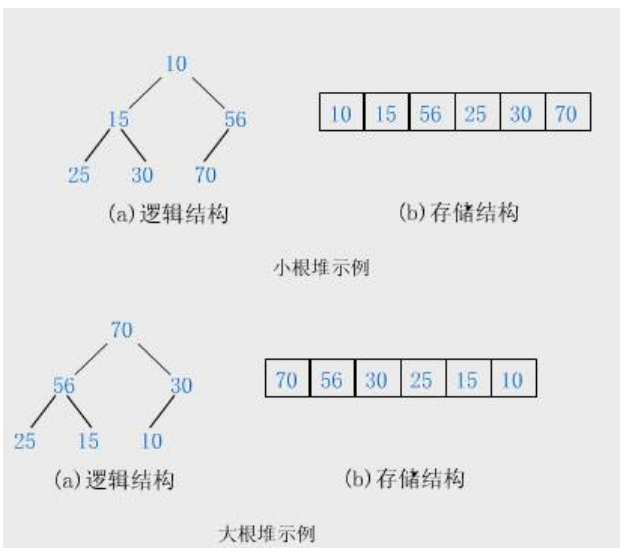
• If I is 0, the node represented by I is the root node, otherwise the parents of node i are (i-1)/2
• If 2*i+1 is less than the number of nodes, the left child subscript of node i is 2*i+1, otherwise there is no left child
• If 2*i+2 is less than the number of nodes, the subscript of the right child of node i is 2*i+2, otherwise there is no right child

Upward adjustment

Upward adjustment process (minimum heap)

1. First, set the penultimate leaf node as the current node and mark it as cur. Find out its parent node and mark it with parent
2. Compare the values of parent and cur. If cur is smaller than parent, it does not meet the rule of small top heap and needs to be exchanged. If cur is larger than parent, it will not be exchanged. At this time, the adjustment is over
3. If the condition is not met, after the exchange, cur will be reset to the subscript of the parent node and the cycle will be restarted. Then check whether the property of the minimum heap is met until the condition is met or cur is less than or equal to 0

Downward adjustment

1. First, set the root node as the current node, mark it as cur, compare the values of the left and right subtrees, find out the smaller value, and mark it with child
2. Compare the values of child and cur. If child is smaller than cur, it does not meet the rule of small heap and needs to be exchanged. If cur is larger than parent, it will not be exchanged. At this time, the adjustment is over
3. If the condition is not met, after the exchange, cur will be reset to the child node subscript and the cycle will be restarted. Then check whether the property of the minimum heap is met until the condition is met or cur is less than or equal to 0

Heap creation (adjust up)

When we have an array that does not meet the heap structure requirements, we need to adjust from the subtree of the penultimate non leaf node to the tree of the root node

ArrayList<Integer> integers = new ArrayList<>();
        integers.add(95);
        integers.add(9);
        integers.add(14);
        integers.add(48);
        integers.add(29);
        integers.add(53);
        integers.add(0);
//        integers.add(5);
        PriorityQueue<Integer> queue1 = new PriorityQueue<>(integers);
        

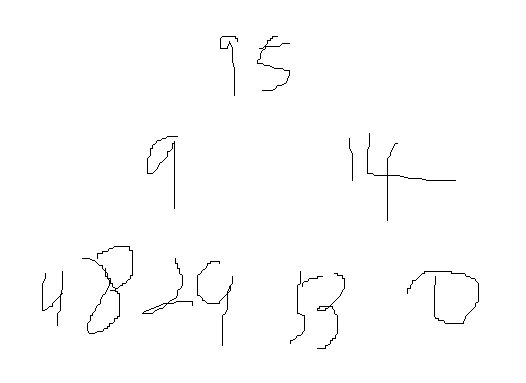
The initial arraylist array element is transformed into a complete binary tree in the form shown in the figure above

Heap adjustment

There are two key methods

    private void heapify() {
        for (int i = (size >>> 1) - 1; i >= 0; i--)
            siftDown(i, (E) queue[i]);
    }

The passed in parameter shifts size to the right without sign > > > 1 and - 1

>>>Move right without symbol:

After moving to the right, the empty bits on the left are filled with zeros. Bits moved out to the right are discarded

The initial size is 7 (0111), and the parameter i passed in after operation is 3 (0011) - 1 = 2

 private void siftDownComparable(int k, E x) {
        Comparable<? super E> key = (Comparable<? super E>)x;
        int half = size >>> 1;        // loop while a non-leaf
        while (k < half) {
            int child = (k << 1) + 1; // assume left child is least
            Object c = queue[child];
            int right = child + 1;
            if (right < size &&
                ((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)
                c = queue[child = right];
            if (key.compareTo((E) c) <= 0)
                break;
            queue[k] = c;
            k = child;
        }
        queue[k] = key;
    }

From the perspective of debugging process

• half is 3
• k is the parameter i passed in from the previous method, and the value is 2
• child is (k < < 1 +) 1 = 5 and reght is 6, respectively

The rule of moving left only remembers one thing: discard the highest bit, and 0 makes up the lowest bit

Heap insertion

The insertion process is to insert the data into the end of the array, and then adjust it upward

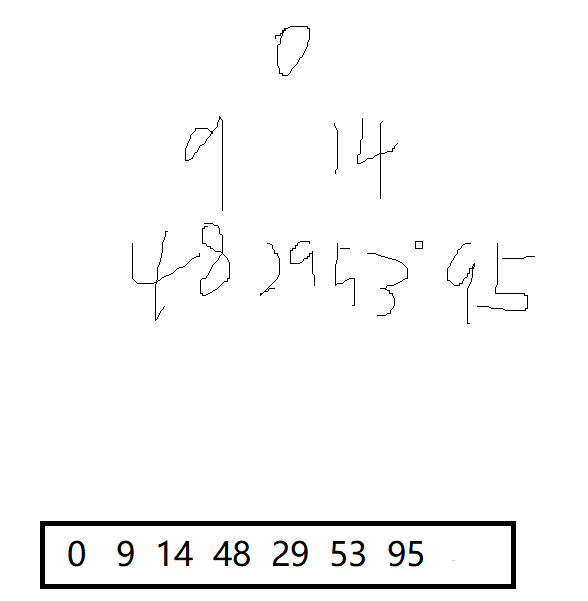
• Suppose you have these elements in the heap before adding element 5
• Now add element 5

 private void siftUpComparable(int k, E x) {
        Comparable<? super E> key = (Comparable<? super E>) x;
        while (k > 0) {
            int parent = (k - 1) >>> 1;
            Object e = queue[parent];
            if (key.compareTo((E) e) >= 0)
                break;
            queue[k] = e;
            k = parent;
        }
        queue[k] = key;
    }

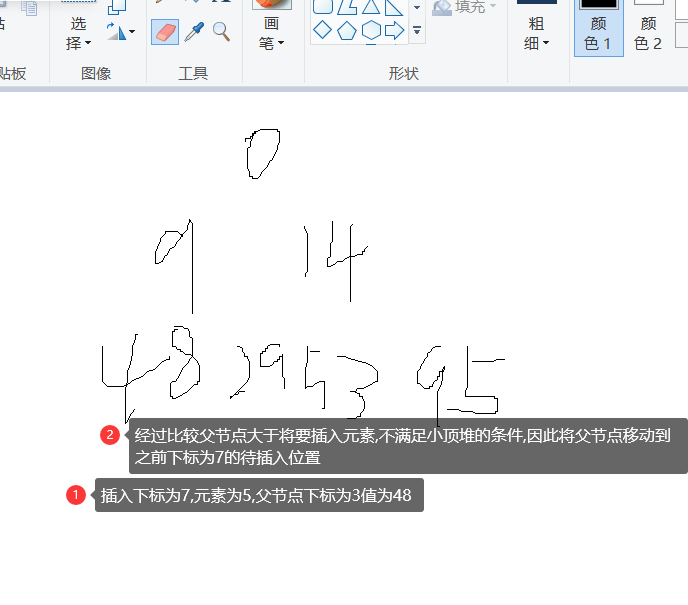
• First, the value of k is 7, which is the subscript of the element to be inserted. If the condition > 0 is met, enter the while loop
• The subscript of the parent element of the parent node is (k-1) > > > 1 is 3, and the value of the corresponding element e is 48
• Then use the compareTo method to compare e with the element key to be inserted (ascII table)
• If the parent node element 48 is large, the compareTo method returns a negative number (returns the ASCII code difference of the first character),
• Therefore, move the parent node element down first, set the value of k as the subscript of the parent node and the subscript of the element to be inserted, and then judge the next cycle until it reaches the top of the heap to end the cycle
• Then put the key value in the corresponding position in the heap

Deletion of heap

The deletion of the heap is a value, which deletes the data at the top of the heap. The process is to exchange the data at the top of the heap with the last data, then delete the last data and adjust the algorithm downward

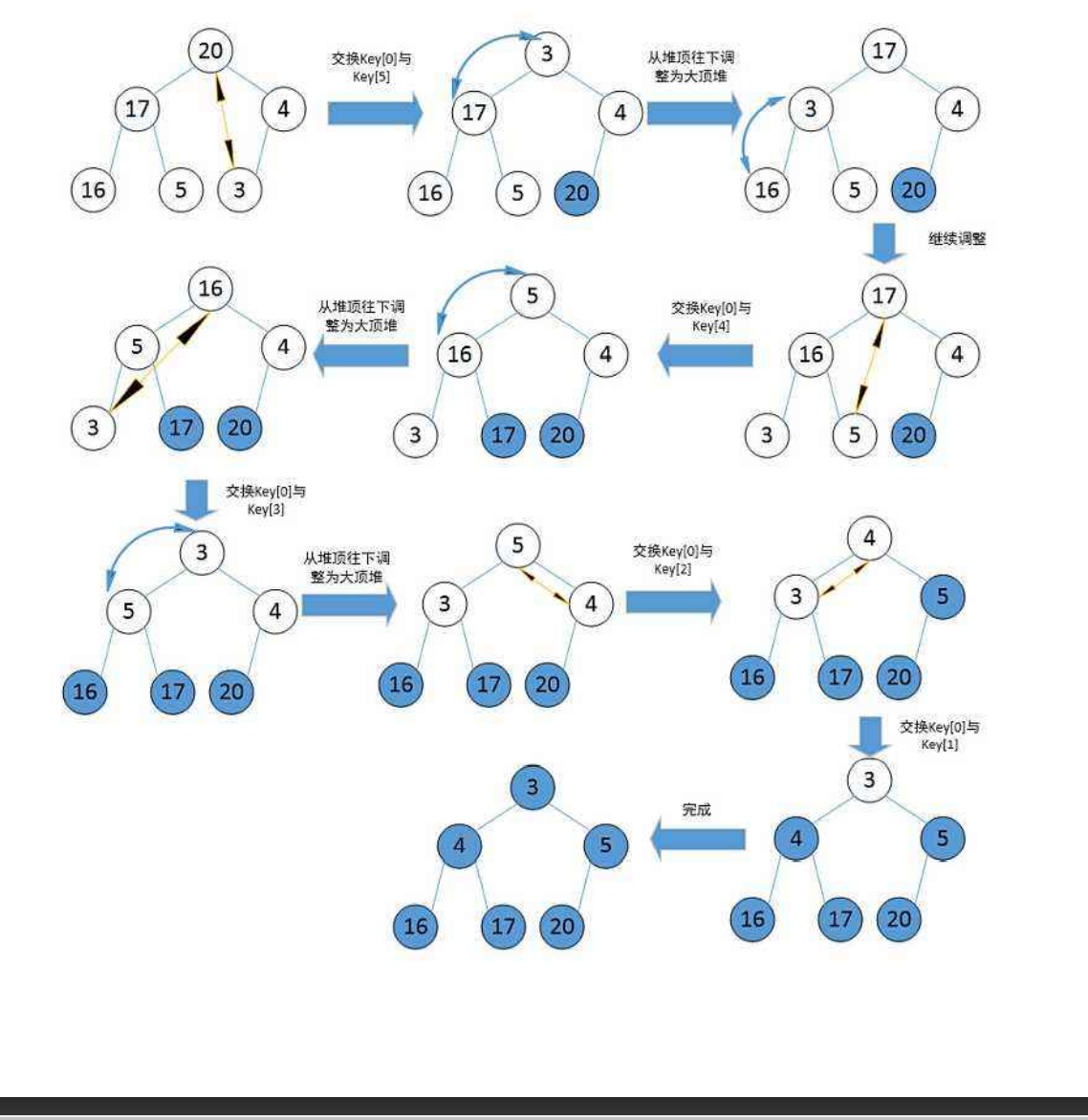
Heap sort

Ascending – large top reactor

1. The sequence to be sorted is constructed into a large top heap
2. At this point, the maximum value of the whole sequence is the root node at the top of the heap.
3. Swap it with the end element, where the end is the maximum.
4. Then reconstruct the remaining n-1 elements into a heap, which will get the sub small value of n-1 elements. If you execute it repeatedly, you can get an ordered sequence.

package Classroom code.data structure.Courseware practice.heap;

public class MyHeaphigh {

    int[] queue = new int[1000];
    int size = 0;

    //Heap sort
    public void hepsort(int[] array) {
        createheap(array);
        for (int i = 0; i < queue.length - 1; i++) {
            size--;
            swap(0, size);
            shftdown(0);
        }
        size = array.length;
    }

    //Adjust array to heap
    public void createheap(int[] array) {
        queue = array;
        size = array.length;
        for (int i = (queue.length - 2) >> 1; i >= 0; i--) {
            shftdown(i);
        }
    }

    //Add element offer
    // Upward adjusted
    public boolean offer(int e) {
        int i = this.size;
        this.size = i + 1;
        queue[i] = e;
        shftup(i);
        return true;
    }

    //Large top heap ascending

    //Downward adjustment
    private void shftdown(int parent) {
        /**
         * The first step is to calculate the left child node and the right child node, and select the smallest as the child node
         * The parent node and child node are exchanged, and the cycle starts from the child node
         */
        int left = parent * 2 + 1, right;
        while (left < size) {
            right = left + 1;
            if (right < size && queue[left] < queue[right]) {
                left++;
            }
            if (queue[parent] > queue[left]) {
                break;
            } else {
                swap(parent, left);
            }
            parent = left;
            left = parent * 2 + 1;
        }
    }

    //Upward adjustment
    private void shftup(int child) {
        while (child > 0) {
            int parent = (child - 1) >> 1;
            if (queue[parent] > queue[child]) {
                break;
            } else {
                swap(child, parent);
                child = parent;
            }
        }
    }

    //Delete element remove
    public void remove() {
        //The deleted element is the stack top element
        // First swap the top element with the last one, and then adjust it down
        swap(0, --size);

        shftdown(0);
    }


    private void swap(int left, int right) {
        int temp = queue[left];
        queue[left] = queue[right];
        queue[right] = temp;
    }
}
//sort

Descending - small top reactor

package Classroom code.data structure.Courseware practice.heap;

public class MyHeaplow {
    int[] queue = new int[1000];
    int size = 0;

    //Heap sort
    public void hepsort(int[] array){
        createheap(array);
        for (int i = 0; i < queue.length-1; i++) {
            size--;
            swap(0,size);
            shftdown(0);
        }
        size=array.length;
    }

    //Adjust array to heap
    public void createheap(int[] array) {
        queue = array;
        size = array.length;
        for (int i = (queue.length-2)>>1; i >=0 ; i--) {
            shftdown(i);
        }
    }

    //Add element offer
    // Upward adjusted
    public boolean offer(int e) {
        int i = this.size;
        this.size = i + 1;
        queue[i] = e;
        shftup(i);
        return true;
    }

    //Descending order of small top reactor
    //Downward adjustment
    private void shftdown(int parent) {
        /**
         * The first step is to calculate the left child node and the right child node, and select the smallest as the child node
         * The parent node and child node are exchanged, and the cycle starts from the child node
         */
        int left = parent * 2 + 1, right;
        while (left < size) {
            right = left + 1;
            if (right < size && queue[left] > queue[right]) {
                left++;
            }
            if (queue[parent] < queue[left]) {
                break;
            } else {
                swap(parent, left);
            }
            parent = left;
            left = parent * 2 + 1;
        }
    }

    //Upward adjustment
    private void shftup(int child) {
        while (child > 0) {
            int parent = (child - 1)>>1;
            if (queue[parent] < queue[child]) {
                break;
            } else {
                swap(child, parent);
                child = parent;
            }
        }
    }

    //Delete element remove
    public void remove() {
        //The deleted element is the stack top element
        // First swap the top element with the last one, and then adjust it down
        swap(0,--size);
//        queue[0] = queue[--size];
        shftdown(0);
    }


    private void swap(int left, int right) {
        int temp = queue[left];
        queue[left] = queue[right];
        queue[right] = temp;
    }
}

The large top heap corresponds to descending order and the small top heap corresponds to ascending order, in which only the elements change. The comparison method is used for comparison

topk problem

What is the topk problem? Here are some examples

1. Given 100 int numbers, find the maximum 10;
2. Given 1 billion int numbers, find the largest 10 (these 10 numbers can be out of order);
3. Given 1 billion int numbers, find the largest 10 (these 10 numbers are sorted in order);
4. Given 1 billion non repeating int numbers, find the largest 10;
5. Given 10 arrays, each array has 100 million int numbers, and find the largest 10 of them;
6. Given 1 billion string type numbers, find the largest 10 (only need to check once);
7. Given 1 billion numbers of string type, find the largest K (you need to query repeatedly, where k is a random number).

What is the idea to solve the problem?

1. Divide and conquer / hash mapping + hash statistics + heap / fast / merge sorting;
2. Double barrel Division
3. Bloom filter/Bitmap；
4. Trie tree / database / inverted index;
5. External sorting;
6. Hadoop/Mapreduce for distributed processing.

1. Massive log data, extract the IP with the most visits to Baidu on a certain day.

Topic analysis

The first method can be used for this problem, divide and conquer / hash mapping + hash statistics + heap / fast / merge sorting

• First of all, for massive data, our memory must not be able to store it. Then we can adopt hash mapping and modular mapping to decompose large files into small files,
• Then the HashMap structure is used for frequency statistics
• After the frequency statistics of each small file are completed, heap sorting or fast sorting can be adopted to get the ip with the most times

Among them, specific analysis is carried out

I. file segmentation

ip is 32 bits, so there are at most 2 ^ 32 different IPs. The essence of IPv4 address is a 32-bit binary string, and an int is also four bytes and 32 bits, so we can use int to store ip,

For an ipv4 address: 192.168.1.3

If the byte is stored with int after removing the decimal point, the maximum value of ipv4 is 255255255255, and the int value range is - 231-231-1, that is - 2147483648-2147483647. Obviously, it can't be stored, so we have to take other ways to store it

First, divide the ip address into 192 168 1 3, then convert it into binary, and then link it. The result is 192 (10) = 11000000 (2); 168(10) = 10101000(2) ; 1(10) = 00000001(2) ; 3(10) = 00000011(2)

The corresponding conversion to int value is - 1062731775

So it can be stored in a variable of type int

Or store it into a long variable, and then take a module of 1000 to divide the whole large file into 1000 small files. (sometimes the ip distribution is not so uniform, so it may need to be divided many times.)

Such a file has such characteristics after being divided. If n files are divided

• All records of the same ip will be stored in one file
• Each file can cover up to 2^32/n IPS

II. Statistics

After the file is divided to be stored in memory, you can use a data structure such as HashMap < integer, long > for statistics,

Three sort

Heap sort each divided small file (this problem only requires the most, and traversal can be used), select the element that appears the most times, and then store the result in another appropriate place. After sorting all small files, we will have n key value pairs, and then sort them

2. The search engine will record all search strings used by users for each search through log files, and the length of each query string is 1-255 bytes. Find the 10 most popular search strings

Topic analysis

Suppose there are 10 million records at present (the repetition of these query strings is relatively high, although the total number is 10 million, but if the repetition is removed, it will not exceed 3 million. The higher the repetition of a query string, the more users query it, that is, the more popular it is.) please count the 10 most popular query strings, and the memory required should not exceed 1G.

I. statistics

Because the string repetition of the query is relatively high, the data set is estimated. If the last repeated result set is small, it can not be divided, but directly use hashmap for statistics

Two sort

Finally, sort the heap, create a 10 size small top heap, traverse the data, and find the ten key s with the largest value

3. There is a 1G file, in which each line is a word. The size of the word does not exceed 16 bytes, and the memory limit is 1M. Returns the 100 words with the highest frequency.

Topic analysis

The memory is 1M, so in order to process these data, we need to divide it into 1024 small files at least to store it in memory. One word is 16 bytes,