Preparatory knowledge
Heap sort
Heap sort is a sort algorithm designed by using the data structure of heap. Heap sort is a selective sort. Its worst, best, average time complexity is O(nlogn), and it is also an unstable sort. First, simply understand the lower heap structure.
heap
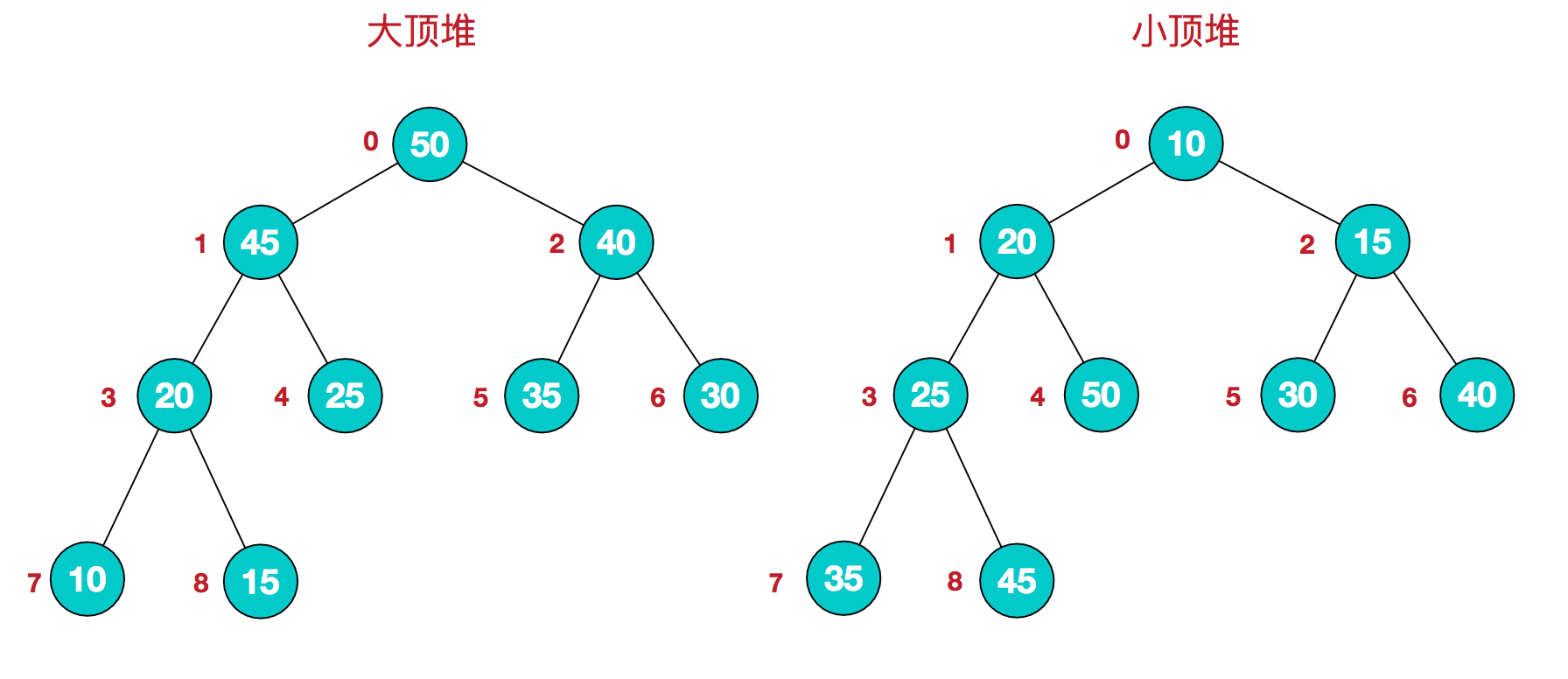
Heap is a complete binary tree with the following properties: the value of each node is greater than or equal to the value of its left and right child nodes, which is called large top heap; Or the value of each node is less than or equal to the value of its left and right child nodes, which is called small top heap. As shown below:
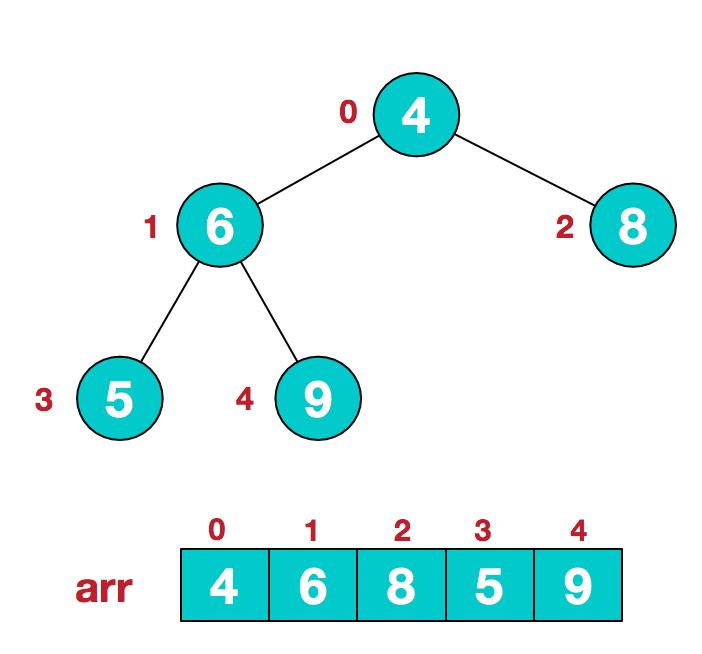
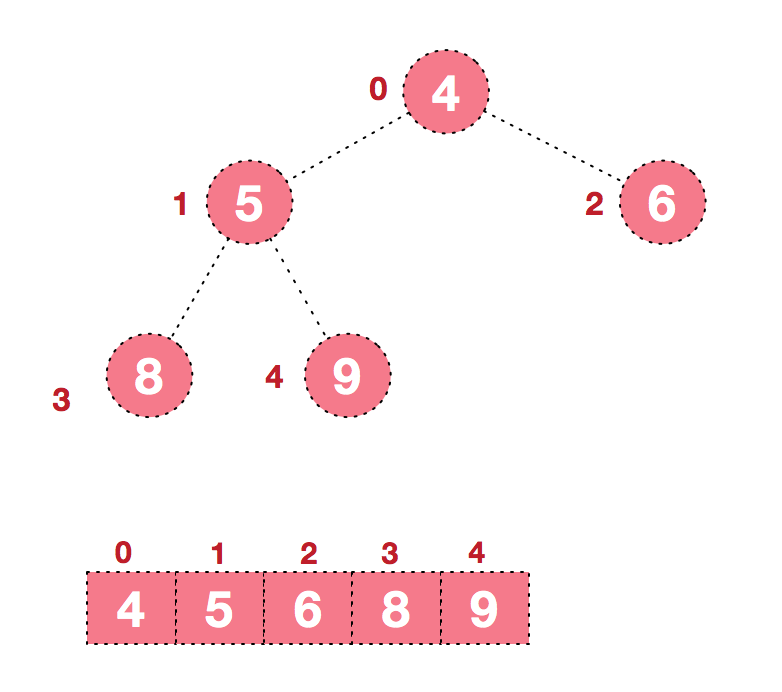
At the same time, we number the nodes in the heap by layer, and map this logical structure to the array, as shown below

Logically speaking, the array is a heap structure. We use a simple formula to describe the definition of heap, which is:
Large top stack: arr [i] > = arr [2I + 1] & & arr [i] > = arr [2I + 2]
Small top pile: arr [i] < = arr [2I + 1] & & arr [i] < = arr [2I + 2]
ok, I understand these definitions. Next, let's look at the basic idea and steps of heap sorting:
Basic idea and steps of heap sorting
The basic idea of heap sorting is to construct the sequence to be sorted into a large top heap. At this time, the maximum value of the whole sequence is the root node at the top of the heap. Swap it with the end element, where the end is the maximum. Then reconstruct the remaining n-1 elements into a heap, which will get the sub small value of n elements. If you execute it repeatedly, you can get an ordered sequence
Step 1: construct the initial heap. The given disordered sequence is constructed into a large top heap (generally, the large top heap is used in ascending order and the small top heap is used in descending order).
A. assume that the structure of a given unordered sequence is as follows
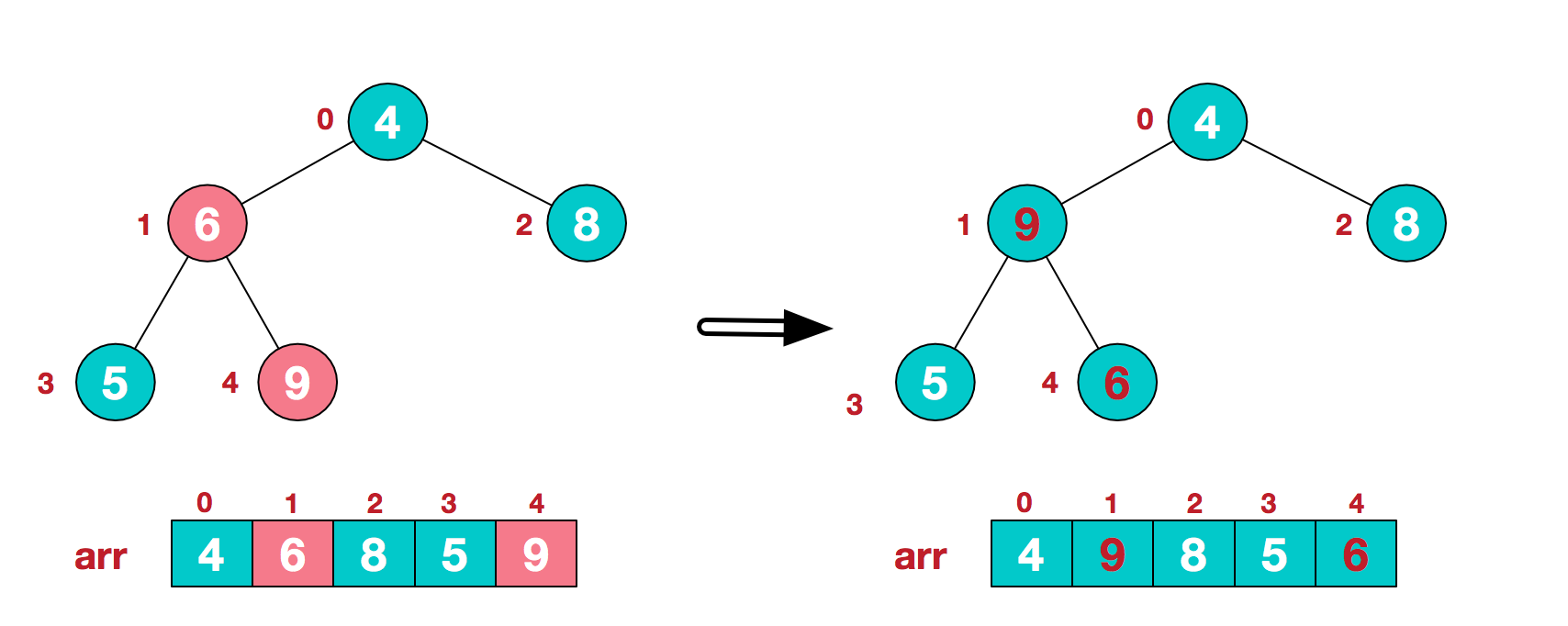
2. At this time, we start from the last non leaf node (the leaf node does not need to be adjusted naturally. The first non leaf node arr.length/2-1=5/2-1=1, that is, the following 6 nodes), and adjust from left to right and from bottom to top.
4. Find the second non leaf node 4. Since 9 elements in [4,9,8] are the largest, 4 and 9 exchange.
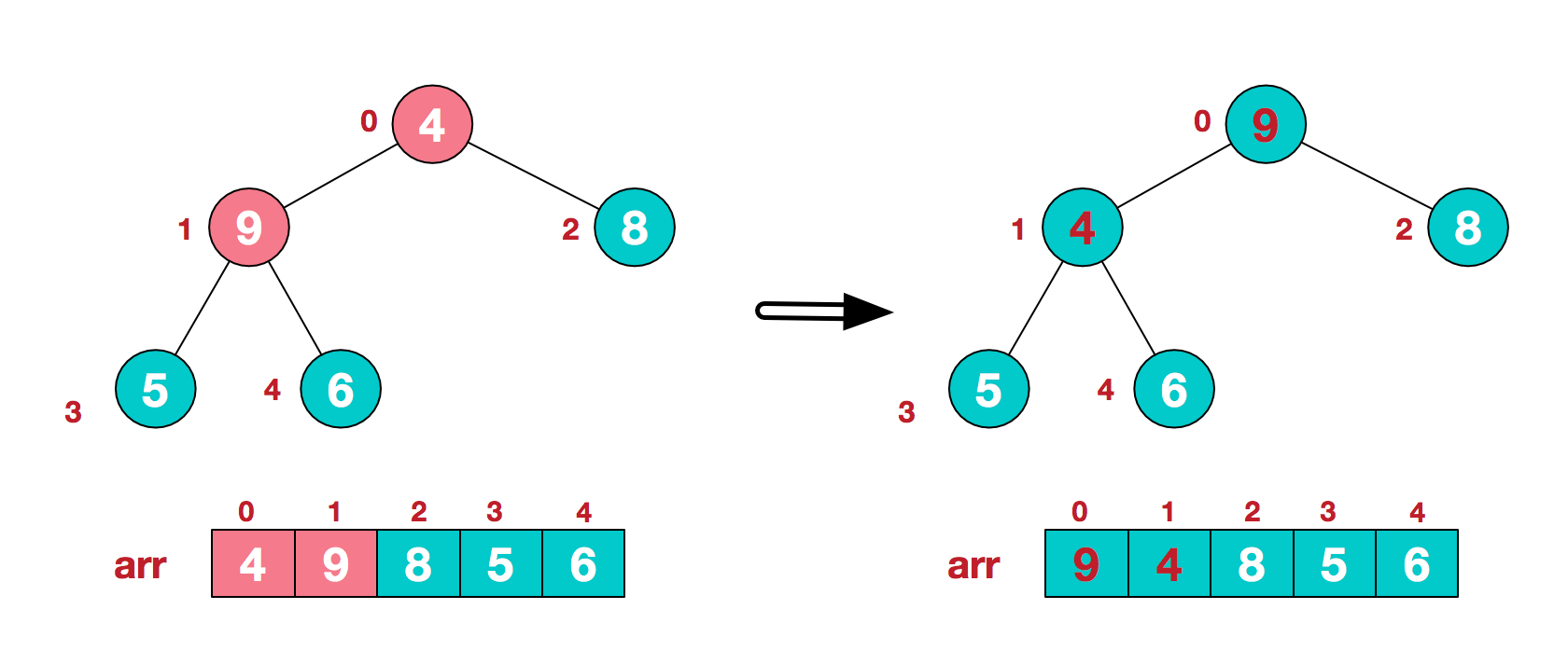
At this time, the exchange leads to the confusion of the structure of the sub root [4,5,6]. Continue to adjust. 6 is the largest in [4,5,6], and exchange 4 and 6.
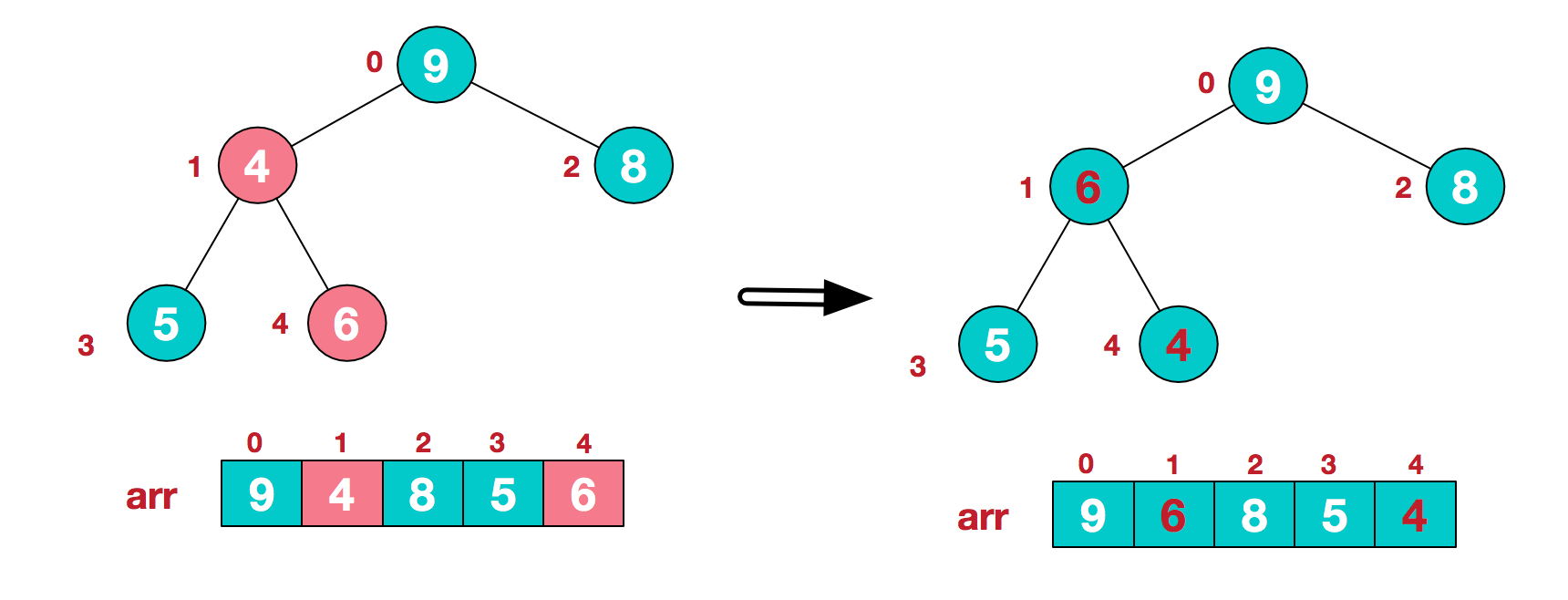
At this point, we construct an unnecessary sequence into a large top heap.
In step 2, the top element of the heap is exchanged with the last element to maximize the last element. Then continue to adjust the heap, and then exchange the top element with the last element to obtain the second largest element. In this way, the exchange, reconstruction and exchange are repeated.
a. Swap top element 9 and end element 4
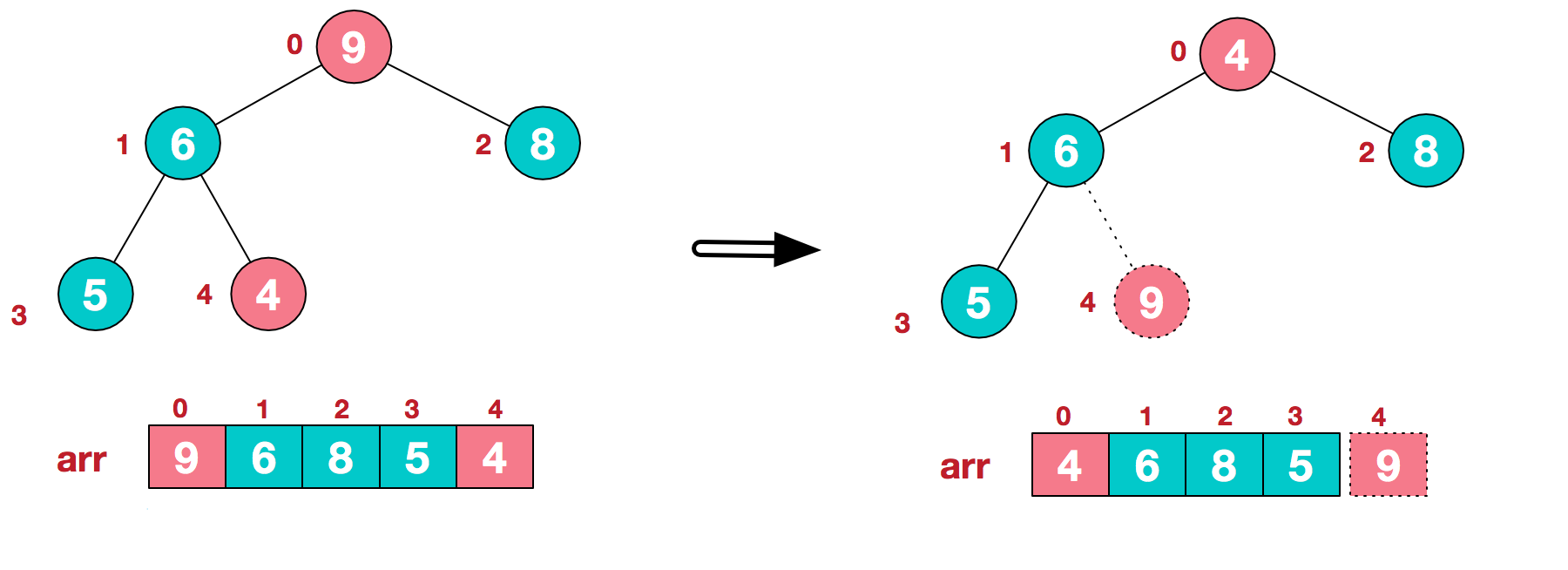
b. Restructure so that it continues to meet the heap definition
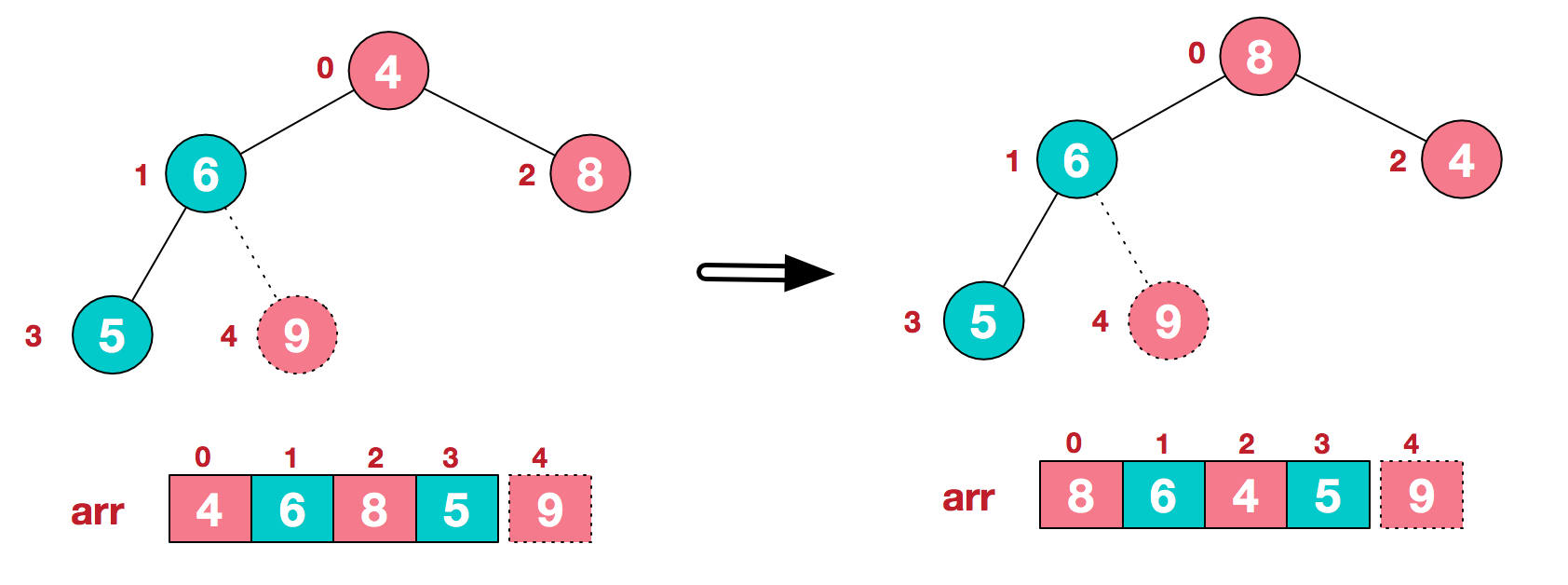
c. Then exchange the top element 8 with the end element 5 to obtain the second largest element 8
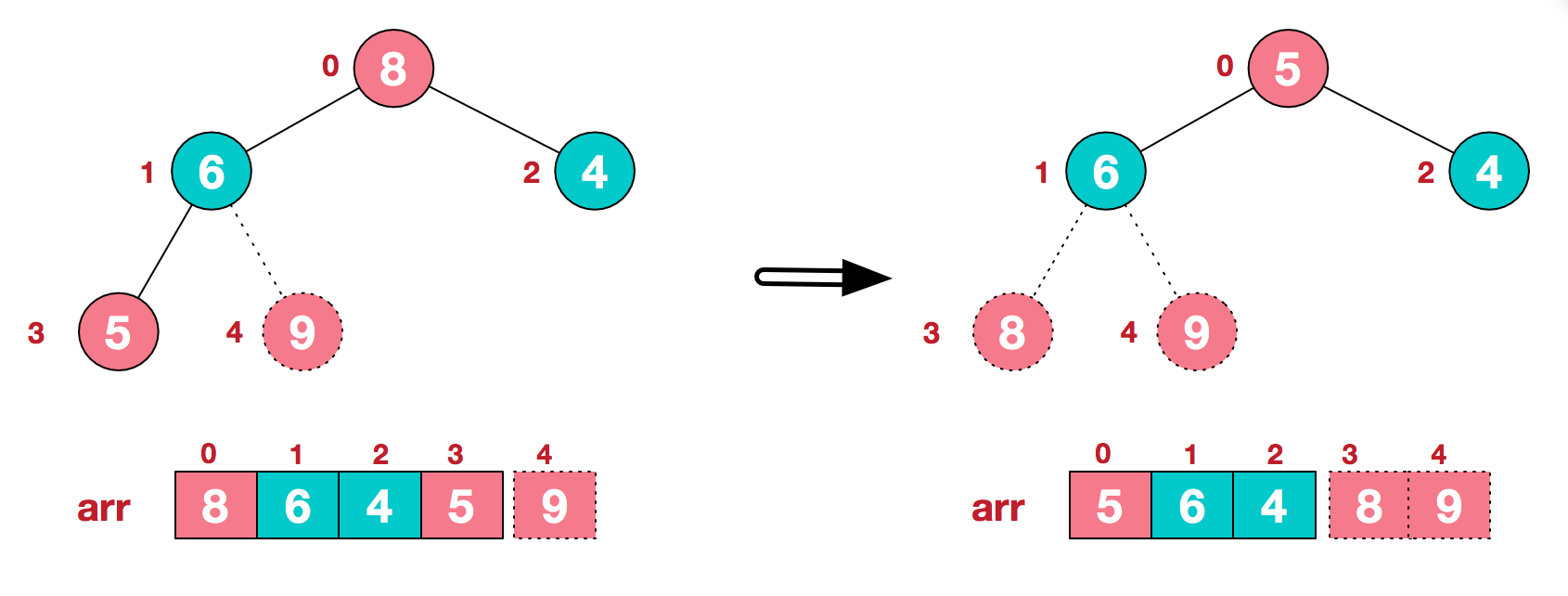
In the subsequent process, continue to adjust and exchange, so as to make the whole sequence orderly
Then briefly summarize the basic idea of heap sorting:
A. build the unnecessary sequence into a heap, and select the large top heap or small top heap according to the ascending and descending requirements;
b. exchange the top element with the end element, and "sink" the largest element to the end of the array;
c. readjust the structure to meet the heap definition, then continue to exchange the top elements of the heap with the current tail elements, and repeat the adjustment + exchange steps until the whole sequence is in order.
code implementation
package sortdemo;
import java.util.Arrays;
/**
* Created by chengxiao on 2016/12/17.
* Heap sort demo
*/
public class HeapSort {
public static void main(String []args){
int []arr = {9,8,7,6,5,4,3,2,1};
sort(arr);
System.out.println(Arrays.toString(arr));
}
public static void sort(int []arr){
//1. Build large top reactor
for(int i=arr.length/2-1;i>=0;i--){
//Adjust the structure from the first non leaf node from bottom to top and from right to left
adjustHeap(arr,i,arr.length);
}
//2. Adjust heap structure + exchange top and end elements
for(int j=arr.length-1;j>0;j--){
swap(arr,0,j);//Swap top and end elements
adjustHeap(arr,0,j);//Readjust the heap
}
}
/**
* Adjust the large top reactor (only the adjustment process, based on the construction of the large top reactor)
* @param arr
* @param i
* @param length
*/
public static void adjustHeap(int []arr,int i,int length){
int temp = arr[i];//First take out the current element i
for(int k=i*2+1;k<length;k=k*2+1){//Start from the left child of node i, that is, 2i+1
if(k+1<length && arr[k]<arr[k+1]){//If the left child node is smaller than the right child node, k points to the right child node
k++;
}
if(arr[k] >temp){//If the child node is larger than the parent node, assign the child node value to the parent node (no exchange)
arr[i] = arr[k];
i = k;
}else{
break;
}
}
arr[i] = temp;//Put the temp value in the final position
}
/**
* Exchange element
* @param arr
* @param a
* @param b
*/
public static void swap(int []arr,int a ,int b){
int temp=arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
}
result
[1, 2, 3, 4, 5, 6, 7, 8, 9]
last
Heap sorting is a kind of selective sorting. The whole is mainly composed of building the initial heap + exchanging the top and end elements of the heap and rebuilding the heap. The derivation complexity of building the initial heap is O(n). In the process of exchanging and rebuilding the heap, it needs to be exchanged n-1 times. In the process of rebuilding the heap, according to the properties of the complete binary tree, [log2(n-1),log2(n-2)...1] Decreasing step by step, approximately nlogn. Therefore, the heap sorting time complexity is generally considered to be O(nlogn) level.