heap

Heap is a special kind of data structure in computer science. Heap is usually an array object that can be regarded as a complete binary tree.

The heap always satisfies the following properties:

• The value of a node in the heap is always not greater than or less than the value of its parent node;
• Heap is always a complete binary tree.

The heap with the largest root node is called the maximum heap or large root heap, and the heap with the smallest root node is called the minimum heap or small root heap.

Example (small root heap)

The value of each parent node is less than its left and right nodes

Storage:

Left node subscript of X: 2x
Right node subscript of X: 2x+1

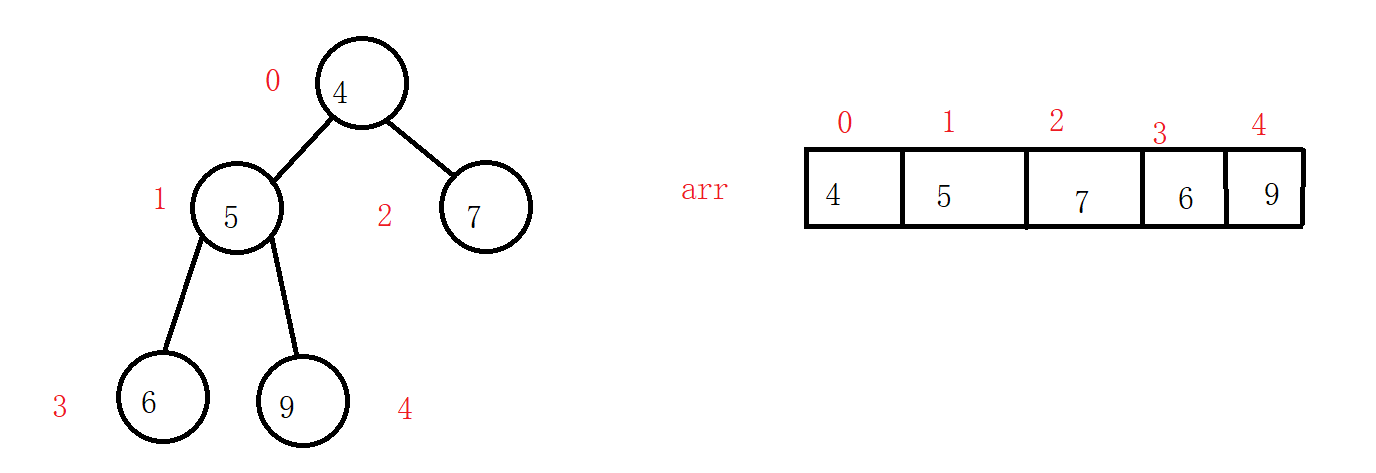
Two methods:

• down: update downward after modifying the data of a node
• up

Template question

Heap sort
Enter an integer sequence with length n, and output the number of the first m from small to large.

Input format
The first line contains integers n and m.

The second row contains n integers, representing the integer sequence.

Output format
A total of one line, including M integers, representing the number of the first m in the integer sequence.

Data range
1≤m≤n≤105，
1 ≤ element in sequence ≤ 109
Input example:

5 3
4 5 1 3 2

Output example:

1 2 3

code

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;

int n, m;
int h[N], cnt;

void down(int u)
{
    int t = u;//Assume that the current node is the smallest node
    if (u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;//If the left node is smaller than the current node
    if (u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;//If the right node is smaller than the current node
    if (u != t)
    {
        swap(h[u], h[t]);//Exchange node value
        down(t);//Because the node exchange may destroy the previous state, you need to continue down to meet the relevant requirements
    }
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &h[i]);
    cnt = n;

    for (int i = n / 2; i; i -- ) down(i);//Build the heap structure quickly, from bottom to top, starting from 2 / n. The reason is that the last layer node itself meets the requirements of the heap and does not need to be processed

    while (m -- )
    {
        printf("%d ", h[1]);
        h[1] = h[cnt -- ];
        down(1);
    }

    puts("");

    return 0;
}

Simple actual combat

Simulated reactor
Maintain a collection. Initially, the collection is empty. The following operations are supported:

I x, insert a number x;
PM, output the minimum value in the current set;
DM, delete the minimum value in the current set (the data ensures that the minimum value at this time is unique);
D k, delete the number of the kth insertion;
C k x, modify the number of the kth insertion to X;
Now, N operations will be performed. For all the second operations, the minimum value of the current set will be output.

Input format
The first line contains the integer N.

Next N lines, each line contains an operation instruction, which is one of I x, PM, DM, D k or C k x.

Output format
For each output instruction PM, a result is output representing the minimum value in the current set.

One line for each result.

Data range
1≤N≤105
−109≤x≤109
The data is guaranteed to be legal.

Input example:

8
I -10
PM
I -10
D 1
C 2 8
I 6
PM
DM

Output example:

-10
6

analysis:

code

#include <iostream>
#include <algorithm>
#include <string.h>

using namespace std;

const int N = 100010;

int h[N], ph[N], hp[N], cnt;//h is the heap, ph[k] represents the subscript of the kth insertion point, and hp is the inverse operation of ph, that is, ph[j]=k,hp[k]=j

void heap_swap(int a, int b)//Switch heap related nodes
{
    swap(ph[hp[a]],ph[hp[b]]);
    swap(hp[a], hp[b]);
    swap(h[a], h[b]);
}

void down(int u)
{
    int t = u;
    if (u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;
    if (u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    if (u != t)
    {
        heap_swap(u, t);
        down(t);
    }
}

void up(int u)
{//If the current node is smaller than the original node after modification, the node needs to be updated upward
    while (u / 2 && h[u] < h[u / 2])
    {
        heap_swap(u, u / 2);
        u >>= 1;
    }
}

int main()
{
    int n, m = 0;
    scanf("%d", &n);
    while (n -- )
    {
        char op[5];
        int k,x;
        scanf("%s", op);
        if (!strcmp(op, "I"))
        {
            scanf("%d", &x);
            cnt ++ ;
            m ++ ;
            ph[m] = cnt, hp[cnt] = m;//The m-th inserted node is subscript cnt, and the m-th inserted node is subscript cnt
            h[cnt] = x;//Storage heap
            up(cnt);
        }
        else if (!strcmp(op, "PM")) printf("%d\n", h[1]);//Output heap top element
        else if (!strcmp(op, "DM"))
        {
            heap_swap(1, cnt);//Delete the heap top element and overwrite it with the last value
            cnt -- ;
            down(1);
        }
        else if (!strcmp(op, "D"))
        {
            scanf("%d", &k);
            k = ph[k];
            heap_swap(k, cnt);
            cnt -- ;
            up(k);//Here, up and down, that is, up and down will only execute one of them. We omit the judgment conditions
            down(k);
        }
        else
        {
            scanf("%d%d", &k, &x);
            k = ph[k];
            h[k] = x;
            up(k);
            down(k);
        }
    }

    return 0;
}