What is a heap?
A heap is a special queue created to handle a particular situation in which the elements are taken out in the order of their priority, not the order in which they are entered.So why organize this form?Since there are various unsatisfactory aspects to sequential storage or chain tables, the average loss is as follows:
So we use full binary tree for storage, so insertion and deletion are O(log(n)), and because it is a full binary tree, it doesn't cause too much waste in space.
Heaps have two characteristics:
(1) Structurality: a complete binary tree represented by an array
(2) Orderliness: The keyword of any node is the maximum or minimum value of all nodes of all its subtrees, corresponding to the maximum or minimum heap, also known as the large or small top heap.
Three important issues of heap concern are deletion, insertion and heap building.
1. Deleting a heap (with the largest heap as an example)
Remove the root node element and delete the root node in the heap at the same time. In order to guarantee the maximum heap quality, we need to transform it. If you select a subtree node value from below to move it up, it will cause a lot of trouble, so we choose to move the last node of the storage array to the root node, and then continueMake a comparison and place it where it should be.
2. Insertion of maximum heap
Place the newly inserted node at the end of the storage array, and we keep comparing it to its parent node, moving it up if it is large, or leaving it in place and ending the insertion.
3. Establishment of maximum heap
There are two ways to store existing N go elements in a one-dimensional array as required by the maximum heap.
(1) Through insertion, one after another is inserted into the initially empty heap at the greatest time cost of O (NlogN).
(2) We can build maximum heaps with linear complexity.
2.1 Stores N elements directly in the input order to satisfy the full binary tree structure
2.2 Adjust the position of each node to satisfy the ordered nature of the maximum heap, starting from the last node with a child node and proceeding forward with a bottom-up adjustment to ensure that the subtree of each adjusted node is the maximum heap, which is the height and time complexity meter of the paths in the treeThe calculation is as follows: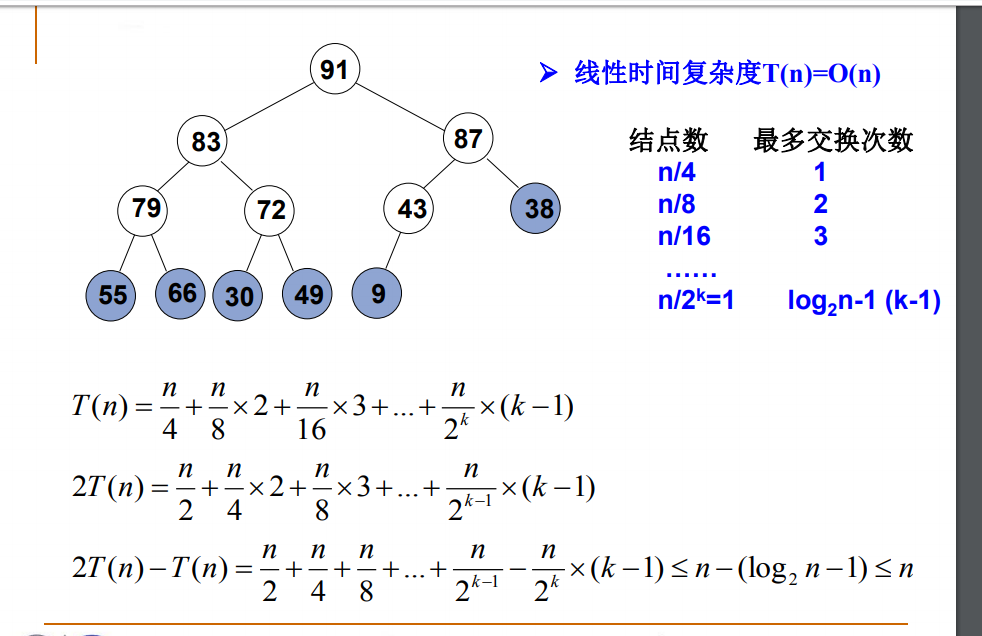
It's O (nlogn) in terms of code and graphics alone, but as we said, it's a bottom-up process, so it becomes O (n).
A complete binary tree with N nodes has at most log2(n+1) layers (rounding down). We set it to H. There are at most 2e(j-1) nodes in the jth layer of the tree. The number of possible downward swaps per layer is reduced by one, so the maximum number of root nodes is reduced by one.So the maximum number of comparisons for each node is h-j, where j is its own layer and H is the total number of layers. The number of comparisons for the second-to-last node is 1*2^(h-1) times (compared with the left and right children, so multiplied by 2). Since bottom-top builds the heap, it doesn't need to be different when adjusting the upper elements.All the lower elements need to be compared only with one of the branches, and the number of comparisons is the height of the tree minus the height of the current node.Therefore, the calculation amount of layer x element is 2^(x)*(h-x), and the general formula above shows that the exact time complexity of constructing a binary heap with tree height h is:
S = 2^(h-1) × 1 + 2^(h-2) × 2 + ...... +1 × (h-1) ①
By observing the above formulas, we can see that the summation formula is the product of equal difference and equal ratio columns. Therefore, to reduce the solution by dislocation, multiply the left and right sides of the formula by two at the same time, we can see that:
2S = 2^h × 1 + 2^(h-1) × 2+ ...... +2 × (h-1) ②
Subtract 1 from 2 to get: S =2^h+2^(h-1)+...- h +13
Bring h = n into the 3 and draw the following conclusions:
S =2n-log(n+1)+1= O(n)
The code for the above operation is as follows:
#include<stdio.h>
#include<stdlib.h>
typedef int ElementType;
typedef struct HNode *Heap; /* Type definition of heap */
#define BOOL int
#define true 1
#define false 0
struct HNode {
ElementType *Data; /* Array storing elements */
int Size; /* Number of current elements in heap */
int Capacity; /* Maximum heap capacity */
};
typedef Heap MaxHeap; /* Maximum heap */
typedef Heap MinHeap; /* Minimum heap */
#define MAXDATA 1000 /* This value should be defined as greater than the value of all the elements in the heap */
MaxHeap CreateHeap( int MaxSize )
{ /* Create an empty maximum heap with a capacity of MaxSize */
MaxHeap H = (MaxHeap)malloc(sizeof(struct HNode));
H->Data = (ElementType *)malloc((MaxSize+1)*sizeof(ElementType));
H->Size = 0;
H->Capacity = MaxSize;
H->Data[0] = MAXDATA; /* Define Sentry to be greater than all possible elements in the heap*/
return H;
}
int IsFull( MaxHeap H )
{
if(H->Size == H->Capacity)
return 1;
return 0;
}
int Insert( MaxHeap H, ElementType X )
{ /* Insert element X into the maximum heap H, where H->Data[0] is already defined as a Sentry */
int i;
if ( IsFull(H) ) {
printf("Maximum heap full");
return 0;
}
i = ++H->Size; /* i Point to the last element in the inserted heap */
for ( ; H->Data[i/2] < X; i/=2 )
H->Data[i] = H->Data[i/2]; /* Up-filter X */
H->Data[i] = X; /* Insert X */
return 1;
}
#Define ERROR-1 /* Error identifiers should be defined as element values that are unlikely to occur in the heap*/
int IsEmpty( MaxHeap H )
{
if(H->Size==0)
return true;
return false;
}
ElementType DeleteMax( MaxHeap H )
{ /* Remove the element with the largest key value from the maximum heap H and delete a node */
int Parent, Child;
ElementType MaxItem, X;
if ( IsEmpty(H) ) {
printf("Maximum heap is empty");
return ERROR;
}
MaxItem = H->Data[1]; /* Remove the maximum value stored at the root node */
/* Filter the lower nodes up from the root with the last element in the maximum heap */
X = H->Data[H->Size--]; /* Note that the size of the current heap is reduced */
for( Parent=1; Parent*2<=H->Size; Parent=Child ) {
Child = Parent * 2;
if( (Child!=H->Size) && (H->Data[Child]<H->Data[Child+1]) )
Child++; /* Child Larger pointing to left and right child nodes */
if( X >= H->Data[Child] ) break; /* Find the right place */
else /* Down-filter X */
H->Data[Parent] = H->Data[Child];
}
H->Data[Parent] = X;
return MaxItem;
}
/*----------- Build the largest heap---------*/
void PercDown( MaxHeap H, int p )
{ /* Filtering down: Adjust the subheap in H rooted in H->Data[p] to the maximum heap */
int Parent, Child;
ElementType X;
X = H->Data[p]; /* Remove the value stored at the root node */
for( Parent=p; Parent*2<=H->Size; Parent=Child ) {
Child = Parent * 2;
if( (Child!=H->Size) && (H->Data[Child]<H->Data[Child+1]) )
Child++; /* Child Larger pointing to left and right child nodes */
if( X >= H->Data[Child] ) break; /* Find the right place */
else /* Down-filter X */
H->Data[Parent] = H->Data[Child];
}
H->Data[Parent] = X;
}
void BuildHeap( MaxHeap H )
{ /* Adjust elements in H->Data[] to satisfy maximum heap ordering*/
/* It is assumed that all H->Size elements already exist in H->Data[] */
int i;
/* From the parent of the last node to the root node 1 */
for( i = H->Size/2; i>0; i-- )
PercDown( H, i );
}
void Show(MaxHeap p)
{
int len=p->Size;
for(int i=1;i<=len;i++)
printf("%d ",p->Data[i]);
printf("\n");
}
void main()
{
MaxHeap p=CreateHeap(20);
Insert(p,44);
Insert(p,33);
Insert(p,7);
Insert(p,6);
Insert(p,99);
Insert(p,12);
Insert(p,999);
Insert(p,54);
Insert(p,34);
Insert(p,15);
Show(p);
DeleteMax( p);
DeleteMax( p);
Show(p);
printf("\n");
MaxHeap p1= CreateHeap(15);
int a[]={55,79,66,83,72,30,49,91,87,43,9,38};
int len=sizeof(a)/sizeof(int);
p1->Size=len;
for(int i=0;i<len;i++)
p1->Data[i+1]=a[i];
Show(p1);
BuildHeap(p1);
Show(p1);
system("pause");
}
Run result:
What are Huffman codes and Huffman trees?
When searching or encoding data, simply viewing each data as an operation of equal probability, regardless of the frequency of data occurrence, will result in a waste of resources. The purpose of Hafman tree is to solve this problem.
Definition of a Huffman tree:
Weighted Path Length (WPL): If a binary tree has n leaf nodes, each leaf node has a weight of w, and the length from the root node to each leaf node is l, then each leaf node
The sum of the weighted path lengths of the points is WPL=w*l (from the first node to the nth node)
Optimal Binary Tree or Huffman Tree: The Minimum Binary Tree of WPL
The construction of a Hafman tree is to merge the two binary trees with the smallest weight each time.
We rely on the smallest heap for implementation, with the following code:
typedef struct TreeNode *HuffmanTree;
struct TreeNode{
int Weight;
HuffmanTree Left, Right;
}
HuffmanTree Huffman( MinHeap H )
{ /* Assume that H->Size weights already exist in H->Elements[]->Weight */
int i; HuffmanTree T;
BuildMinHeap(H); /*Adjust H->Elements[] to minimum heap by weight*/
for (i = 1; i < H->Size; i++)
{ /*Make H->Size-1 merge*/
T = malloc( sizeof( struct TreeNode) ); /*Create a new node*/
T->Left = DeleteMin(H);
/*Remove a node from the minimum heap as the left child of the new T*/
T->Right = DeleteMin(H);
/*Remove a node from the minimum heap as the right child of the new T*/
T->Weight = T->Left->Weight+T->Right->Weight;
/*Calculate new weight*/
Insert( H, T ); /*Insert new T into minimum heap*/
}
T = DeleteMin(H);
return T;
}
The overall complexity is O(NlogN).
The characteristics of the Huffman tree:
(1) There is no node with degree 1
(2) A Hafman tree with n leaf nodes has 2n-1 nodes
(3) The left and right subtrees of any non-leaf node of a Huffman tree are swapped and thrown away as a Huffman tree.
(4) For a set of data with the same weight, there are two Huffman trees with different structures.
The most important thing for unequal-length encoding like Huffman encoding is to avoid ambiguity. The encoding of any character must not be a prefix of another character encoding in order to decode without ambiguity. According to this feature, we use binary trees to encode according to the following two conditions:
(1) The left and right branches are 0 and 1, respectively.
(2) Characters are only on leaf nodes.