Hello, I'm Monday.

Today we talk about heap and heap sorting.

1, Pile

When it comes to heaps, we should first start with binary trees, from binary trees to complete binary trees, and then to heaps.

1. Binary tree

Each node can only have two subtrees at most, and can be divided into left and right

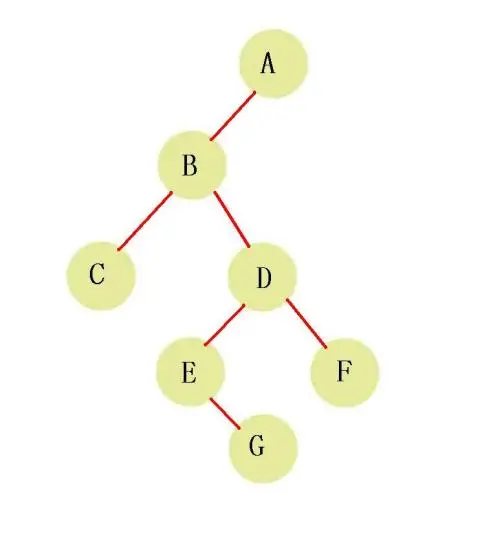
2. Complete binary tree

For a binary tree with n nodes with depth k, the nodes in the tree are numbered from top to bottom and from left to right. If the node numbered i (1 ≤ i ≤ n) is in the same position in the binary tree as the node numbered i in the full binary tree (except for the binary tree with no child nodes in the last layer, all nodes on each layer have two child nodes), Then this binary tree is called a complete binary tree.

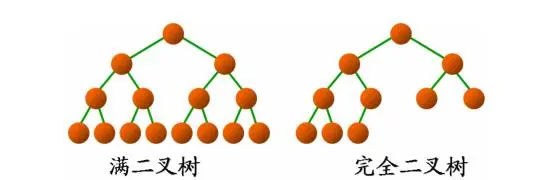
The popular saying is that leaf nodes can only appear in the lowest and sub lower layers, and the leaf nodes in the lowest layer are concentrated on the left of the tree. It should be noted that a full binary tree must be a complete binary tree, and a complete binary tree is not necessarily a full binary tree.

For a node with position I, the left child (if any) 2i+1, the right child (if any) 2i+2, and the parent node (i-1)/2 (rounded down)

3. Pile

The first is a complete binary tree. Distinguish between large root heap and small root heap at the same time.

Large root heap: the maximum value of each subtree is the head node.

Small root heap: the minimum value of each subtree is the head node.

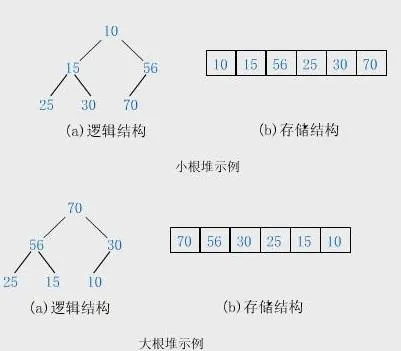
(1) How to construct a large root heap for an array of numbers entered by the user in turn?

Each inserted number is compared with the parent node. If it is greater than the parent node, it is exchanged with the parent node until the root node; If it is smaller than the parent node, the comparison is stopped immediately.

//  For the newly added number of i positions, please put it in the appropriate position of the array to make it a large root heap
private void heapInsert(int[] arr, int i) {
    //  i  =  0   or   I the number of locations is less than the parent node
    //  while contains these two termination conditions
    while(arr[i] > arr[(i - 1)/2]) {
        swap(arr, i, (i - 1)/2);
        i = (i - 1)/2;
    }
}

(2) Get the maximum value of the current array and delete it from the heap while maintaining the large root heap structure

public int pop() {
    int ans = heap[0];
    swap(heap, 0, --heapSize);
    heapify(heap, 0, heapSize);
    return ans;
}

//  Sink the number in the index position until the older children are not as old as themselves or have no children
private void heapify(int[] arr, int index, int heapSize) {
    //  Left subtree position
    int left = 2 * index + 1;
    while(left < heapSize) {        
        //  Find which of the left and right subtrees is more valuable
       int maxIndex = (left + 1) < heapSize && arr[left + 1] > arr[left] ? left + 1 : left;
       //  Compare the larger in the left and right subtrees with the parent node
       maxIndex = arr[maxIndex] > arr[index] ? maxIndex : index;
       //  The larger values of the left and right subtrees are less than the parent node. Stop the cycle      
       if (maxIndex == index) {
           break;
       }
       //  Swap the larger of the left and right subtrees with the parent node
       swap(arr, maxIndex, index);
       //  The node position of the current comparison comes to the larger child node
       index = maxIndex;
       //  Retrieve the left subtree of the current node
       left = 2 * index + 1;
    }
}

4,PriorityQueue

The bottom layer is implemented by heap, and the default is small root heap

5. Time complexity

heapinsert: add a number to the number that is already a heap structure. The time complexity is O(logN)

heapify, add a number to the number that is already a heap structure, and the time complexity is O(logN)

2, Heap sort

1. Adjust the entire array to a large root heap, and the number of positions 0 is the maximum

2. Exchange the number of 0 position and the maximum position of the array, and the maximum value is at the last ordered position

3. Reduce the number of adjustment ranges of the array by one, and cycle through steps 1 and 2 until the array is empty

public static void heapSort(int[] arr) {
    if (arr == null || arr.length < 2) {
        return;
    }
    //  Adjust the entire array to a large root heap, O(NlogN)
    for (int i = 0; i < arr.length; i++) { // O(N)
        heapinsert(arr, i); // O(logN)
    }
    //  Gets the current array size
    int heapSize = arr.length;
    //  The number of swap between the 0 position and the maximum position of the array
    swap(arr, 0, --heapSize);
    while(heapSize > 0) {
        //  Sink the number exchanged to position 0, that is, adjust the current array to a large root heap again
        heapify(arr, 0, heapSize);
        //  The number of swap between the 0 position and the maximum position of the array
        swap(arr, 0, --heapSize);
    }    
}

4. Complexity

(1) Time complexity: O(N*logN)

(2) Additional space complexity: O(1)