subject
Idea: first, build a palindrome tree, and then the problem is how to quickly determine whether the palindrome string represented by a node is the palindrome string required by the title. The violent judgment is to follow the suffix link, and then T emmm. In fact, when inserting a node, we can judge the starting position of the palindrome string represented by it by its length and the current insertion to the first few characters. The starting position is known by L, and the ending position is known by R. the length is len. If we want to meet the problem requirements, that is, the substring of the interval [l,l+(len+1)/2] should also be palindrome string. Here we have a property: if [l,r] It is a palindrome string and [l,l+(len+1)/2] this substring is equal to the substring represented by [r-(len+1)/2 + 1,r], then these two substrings are palindrome strings, as shown in the figure: x represents a certain character, and the characters connected by the same color line are equal; thus, if you look along the line, you will find that the first three characters are palindrome strings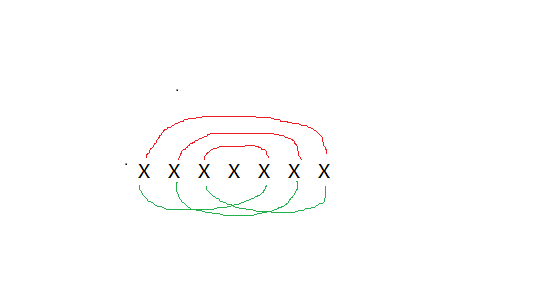

Therefore, with this property + hash, we can O(1) judge whether the string represented by this node meets the requirements.
Another thing I want to throw up is: if the base is larger in hash, for example, 200 is WA
, I don't know. I can understand when I take a small WA, and I can understand when I take a large wa. . ,

#include<bits/stdc++.h>
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<map>
#include<cstring>
#include<queue>
const int maxn = 3e5 + 10;
const int maxm = 1e6 + 10;
const int inf_max = 0x3f3f3f;
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
char str[maxn];
int ans[maxn];
const ull base = 131;
ull fac[maxn],hs[maxn];
ull gethash(int l, int r){
    return hs[r] - hs[l - 1] * fac[r - l + 1];
}
struct HW {
    struct node {
        int len,cnt,ch[26],fail,satisfy;
    }tree[maxn];
    int tot,chnum,last;
    char exsitch[maxn];
    int newnode(int len) {
        int cur = ++tot;
        memset(tree[cur].ch,0,sizeof(tree[cur].ch));
        tree[cur].cnt = tree[cur].fail = tree[cur].satisfy = 0;tree[cur].len = len;
        return cur;
    }
    void Initial() {
        tot = -1;
        newnode(0);newnode(-1);
        tree[0].fail = 1;
        exsitch[chnum = last = 0] = '$';
    }
    int getfail(int x) {
        while(exsitch[chnum] != exsitch[chnum - tree[x].len - 1]) x = tree[x].fail;
        return x;
    }
    void ins(int x) {
        int id = x - 'a';
        exsitch[++chnum] = x;
        int now = getfail(last);
        if(!tree[now].ch[id]) {
            int cur = newnode(tree[now].len + 2);
            tree[cur].fail = tree[getfail(tree[now].fail)].ch[id];
            tree[now].ch[id] = cur;
            int half = (tree[cur].len + 1) / 2;
            if(tree[cur].len == 1 || gethash(chnum - tree[cur].len + 1, chnum - tree[cur].len + half) == gethash(chnum - half + 1, chnum)) tree[cur].satisfy = 1;
            else tree[cur].satisfy = 0;
        }
        last = tree[now].ch[id];
        tree[last].cnt++;
    }
    void solve() {
        for(int i = tot;i >= 0; --i) {
            int f = tree[i].fail,len = tree[i].len;
            tree[f].cnt += tree[i].cnt;
            if(tree[i].satisfy) ans[len] += tree[i].cnt;
        }
    }
}hwauto;
int main()
{
    fac[0] = 1;
    for(int i = 1;i <= 300005; ++i) fac[i] = fac[i - 1] * base;
    while(~scanf("%s",str + 1)) {
        memset(ans,0,sizeof(ans));
        int len = strlen(str + 1);
        hwauto.Initial();
        hs[0] = 0;
        for(int i = 1;i <= len; ++i) hs[i] = hs[i-1] * base + str[i];
        for(int i = 1;i <= len; ++i) hwauto.ins(str[i]);
        hwauto.solve();
        for(int i = 1;i <= len; ++i) {
            printf("%d%c",ans[i],i == len ? '\n' : ' ');
        }
    }
    return 0;
}