Here's the general idea: Give you an n*m matrix of 01. Now let's get rid of a number for each row and column, and ask that the absolute value of the position of the number removed between adjacent rows be less than or equal to k. Now ask you how many kinds of rectangles you can delete.

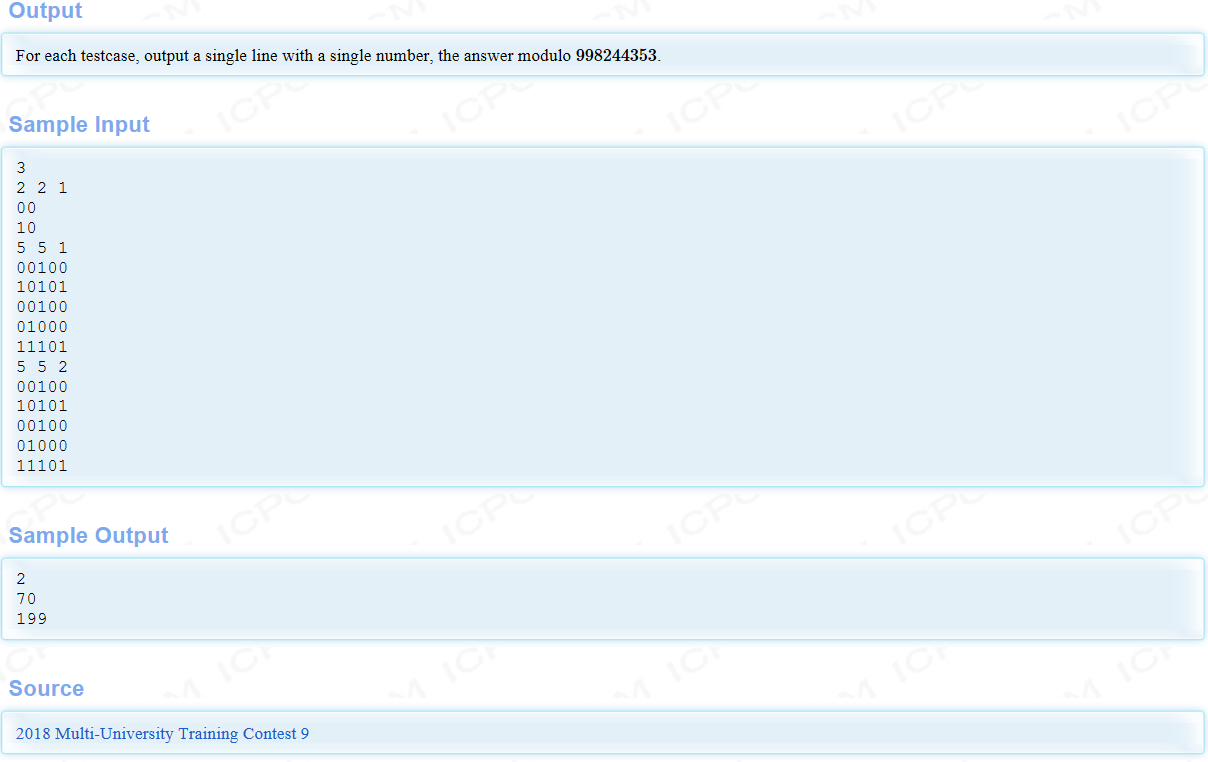
First of all, let's consider one line at a time. For the same line, obviously, it depends on how many blocks there are and how many solutions there are. Then for the whole matrix, any position (i,j) can be transferred from the previous line (j-k,j+k). dp[i][j] denotes the number of schemes that are processed to line I without considering duplication, and that the jth position is deleted from line I. Then, apparently according to the transfer interval mentioned earlier, there is a transfer equation:

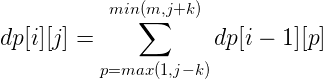
However, there will be repetition, because deleting any one in a piece is the same. So we consider deleting the duplication of these calculations. So how much is this repetition? Let's suppose that the duplicate is ss[i][j], which represents the jth position of line I and the part duplicated with the J1 position of the same line. We consider that the intersection interval of two adjacent locations J and J-1 is [j-k,j-1+k], so our ss[i][j] should also be transferred from the interval of the previous row, of course, to ensure that J and J-1 are in the same block, otherwise J and J-1 will not repeat. Specifically:

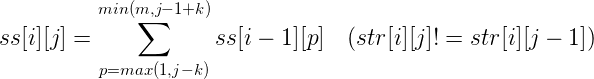
In this way, we will solve this problem. For location (i,j), the number of programs that deal with line I and delete j from line I is dp[i][j]-ss[i][j].

In the case of dp violence, the time complexity is O(N^3), but obviously this can be prefixed and optimized. This complexity can go to O(N^2), and then to save space, my code uses scrolling arrays. See the code specifically:

#include<bits/stdc++.h>
#define LL long long
#define mod 998244353
#define pb push_back
#define lb lower_bound
#define ub upper_bound
#define INF 0x3f3f3f3f
#define sf(x) scanf("%d",&x)
#define sc(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define clr(x,n) memset(x,0,sizeof(x[0])*(n+5))
#define IO ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define file(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout)
using namespace std;

const int N = 2e3 + 10;

int ss[2][N],s[2][N];
char str[N][N];

int main()
{
    int T; sf(T);
    while(T--)
    {
        int n,m,k;
        sc(n,m,k);
        for(int i=1;i<=n;i++)
        {
            str[i][0]='9';
            scanf("%s",str[i]+1);
        }
        int cur=1,pre=0;
        clr(s[pre],m); clr(ss[pre],m);
        for(int i=1;i<=m;i++)
        {
            s[0][i]=1; ss[0][i]=(str[1][i]==str[1][i-1]);
        }
        for(int i=2;i<=n;i++)
        {
            clr(ss[cur],m); clr(s[cur],m);
            for(int j=1;j<=m;j++)
            {
                s[pre][j]=(s[pre][j-1]+s[pre][j])%mod;
                ss[pre][j]=(ss[pre][j-1]+ss[pre][j])%mod;
            }
            for(int j=1;j<=m;j++)
            {
                int l=max(1,j-k),r=min(m,j+k);
                s[cur][j]=(s[pre][r]-s[pre][l-1]+mod)%mod;
                s[cur][j]=(s[cur][j]-(ss[pre][r]-ss[pre][l]+mod)%mod+mod)%mod;
                if (str[i][j]!=str[i][j-1]) {ss[cur][j]=0;continue;}
                r=min(m,j+k-1); ss[cur][j]=(s[pre][r]-s[pre][l-1]+mod)%mod;
                ss[cur][j]=(ss[cur][j]-(ss[pre][r]-ss[pre][l]+mod)%mod+mod)%mod;
            }
            swap(cur,pre);
        }
        LL ans=s[pre][1]%mod;
        for(int i=2;i<=m;i++)
            ans=(ans+s[pre][i]-ss[pre][i]+mod)%mod;
        printf("%lld\n",ans);
    }
    return 0;
}