Problem Description

There are n apples on a tree, numbered from 1 to n.
Count the number of ways to pick at most m apples.

Input

The first line of the input contains an integer T (1≤T≤105) denoting the number of test cases.
Each test case consists of one line with two integers n,m (1≤m≤n≤105).

Output

For each test case, print an integer representing the number of ways modulo 109+7.

meaning of the title

Group T: Ask you C every time.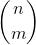， n, m <= 1e5.

Title Solution

No team or block watch.

Preprocess n into block blocks. The formula is deduced from Yang Hui's triangle.

The following is for the above formula to be partitioned.

1. Let's start with the idea of partitioning. Firstly, if there is no block pre-processing, then violence can be 1-n, sum one by one. Blocks are non-explosive forces of 1-n, and every block (blocks are usually n below the root) we seek a summation of violence. For the current n, we look for an answer that has been blocked and violent recently from n, and shift from this answer to n. This reduces the complexity. Of course, for n less than block, direct violence is enough.

2. Represent the prefix sum of C (n, j) with the array sum[i][j]. I start with the block and add each block.

3. Predict violence with d array to get the answer when n < block.

4. Discussed in different situations, n < block directly outputs d[n][m],n%block==0 directly outputs sum[n][m]. In other cases, find out the nearest preprocessed value of Rin, sum[n/block][m]. Then the answer is obtained by recurring to n according to the formula deduced from the second row in the figure above.

#include<stdio.h>
#include<algorithm>
#include<iostream>
#include<string.h>
#include<vector>
#include<stdlib.h>
#include<math.h>
#include<queue>
#include<deque>
#include<ctype.h>
#include<map>
#include<set>
#include<stack>
#include<string>
#define INF 0x3f3f3f3f
#define FAST_IO ios::sync_with_stdio(false)
const double PI = acos(-1.0);
const double eps = 1e-6;
const int MAX=1e5+10;
const int mod=1e9+7;
typedef long long ll;
using namespace std;
#define gcd(a,b) __gcd(a,b)
inline ll lcm(ll a,ll b){return a/gcd(a,b)*b;}
inline ll qpow(ll a,ll b){ll r=1,t=a; while(b){if(b&1)r=(r*t)%mod;b>>=1;t=(t*t)%mod;}return r;}
inline ll inv1(ll b){return qpow(b,mod-2);}
inline ll exgcd(ll a,ll b,ll &x,ll &y){if(!b){x=1;y=0;return a;}ll r=exgcd(b,a%b,y,x);y-=(a/b)*x;return r;}
inline ll read(){ll x=0,f=1;char c=getchar();for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;for(;isdigit(c);c=getchar()) x=x*10+c-'0';return x*f;}
//freopen( "in.txt" , "r" , stdin );
//freopen( "data.txt" , "w" , stdout );
 
int n,m,block=333;
int fac[MAX+3];
int inv[MAX+3];
int sum[100010/333+1][MAX];
int d[400][400];
 
void init()
{
    fac[0]=1;
    for(int i=1;i<=MAX;i++) fac[i]=fac[i-1]*1ll*i%mod;
    inv[MAX]=qpow(fac[MAX],mod-2);
    for(int i=MAX-1;~i;i--) inv[i]=inv[i+1]*1ll*(i+1)%mod;
}
 
int C(int n,int m)
{
    if(m>n) return 0;
    if(m==n || m==0) return 1;
    return fac[n]*1ll*inv[n-m]%mod*inv[m]%mod;
}
 
void fk()
{
    for(int i=block;i<MAX;i+=block)
    {
        ll temp=0;
        for(int j=0;j<MAX;j++)
        {
            temp=(temp+C(i,j))%mod;
            sum[i/block][j]=temp;
        }
    }
 
    for(int i=1;i<block;i++)
    {
        ll temp=0;
        for(int j=0;j<=i;j++)
        {
            temp=(temp+C(i,j))%mod;
            d[i][j]=temp;
        }
    }
}
 
int main()
{
    int t;
    init();
    fk();
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d",&n,&m);
        ll ans=0;
        if(n<block) ans=d[n][m];
        else if(n%block==0) ans=sum[n/block][m];
        else
        {
            ans=2*sum[n/block][m]%mod;
            ans=(ans-C(n/block*block,m))%mod;
 
            for(int i=n/block*block+2;i<=n;i++)
            {
                ans=2*ans%mod-C(i-1,m);
                if(ans<0) ans+=mod;
            }
        }
        printf("%lld\n",(ll)(ans+mod)%mod);
    }
    return 0;
}