Title:
Give you an eight-sided magic cube and ask if you can restore it in three steps.
Train of thought:
A really disgusting topic...
In fact, it is very simple to sort out, although it is very troublesome to write.
If you look at the pictures in the title, the bottom can be rotated, and there are eight sides. First, there are eight operations to rotate the bottom.
The figure also describes the rotation of the intermediate axis, if the middle axis is two planes to determine an intermediate axis, a total of eight planes, so there are four intermediate axes.
Therefore, there are 8 + 4 = 12 rotation operations, plus counter-clockwise, a total of 24 rotation operations.
The counter-clockwise is also quite good. The counter-clockwise operation of rotating the bottom is to turn clockwise twice.
The middle axis is the same. It's easy to write directly.
Then the simulation will do.
But WA always thought that there was something wrong with the rotation (there was a problem), but the mistake was that the dfs was written incorrectly.
I haven't noticed the problem of dfs before, and I've learned a lot from it today.
That is, the number of temporary arrays in dfs should not be too large.
Because it's retrospective, so we need to record what's before it's not turned, but the opening is a 72 int array, which can't give the answer directly... (That should also go back to TLE.)
So in order to avoid repeating open arrays, do not open directly, turn around, turn back counterclockwise, do not record...
Stick some pictures to commemorate it. T_T

Refer to it casually:
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int a[100];
bool check(){
for (int i = 1; i <= 8; ++i){
int st = (i-1)*9 + 1;
for (int j = st; j <= st + 9 - 1; ++j){
if (a[j] != a[st]) return false;
}
}
return true;
}
int a2[100] ;
void rotate1(int b[], int c[]){
int t = a[ b[6] ];
a[b[6] ] = a[b[0] ];
a[b[0] ] = a[b[12] ];
a[b[12] ] = t;
int t1 = a[b[1] ];
int t2 = a[b[2] ];
int t3 = a[b[3] ];
int t4 = a[b[4] ];
int t5 = a[b[5] ];
for (int i = 1; i <= 5; ++i){
a[b[i] ] = a[b[ i + 12] ];
}
for (int i = 13; i < 18; ++i){
a[b[i] ] = a[b[i - 6] ];
}
a[b[7] ] = t1;
a[b[8] ] = t2;
a[b[9] ] = t3;
a[b[10] ] = t4;
a[b[11] ] = t5;
for (int i = 1; i <= 72; ++i){
a2[i] = a[i];
}
a[c[0] ] = a2[c[4] ];
a[c[1] ] = a2[c[6] ];
a[c[2] ] = a2[c[5] ];
a[c[3] ] = a2[c[1] ];
a[c[4] ] = a2[c[8] ];
a[c[5] ] = a2[c[7] ];
a[c[6] ] = a2[c[3] ];
a[c[7] ] = a2[c[2] ];
a[c[8] ] = a2[c[0] ];
}
void rotate2(int d[], int way){
if (way == 0){
int t1 = a[d[15] ];
int t2 = a[d[16] ];
int t3 = a[d[17] ];
for (int i = 15; i >= 3; i -= 3){
for (int j = i; j < i + 3; ++j){
a[d[j] ] = a[d[j-3] ];
}
}
a[d[0] ] = t1;
a[d[1] ] = t2;
a[d[2] ] = t3;
}
else {
int t1 = a[d[0] ];
int t2 = a[d[1] ];
int t3 = a[d[2] ];
for (int i = 0; i <= 12; i += 3){
for (int j = i; j < i + 3; ++j){
a[d[j] ] = a[d[j+3] ];
}
}
a[d[15] ] = t1;
a[d[16] ] = t2;
a[d[17] ] = t3;
}
}
///================================
/// 1:
///0 6 12
///23 64 9
/// 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
int b1[] = {23, 63, 62, 58, 57, 55, 64, 37, 39, 38, 42, 41, 9, 14, 15, 16, 17, 18};
int c1[] = {50, 52, 51, 47, 54, 53, 49, 48, 46};
int b2[] = {19, 10, 12, 11, 15, 14, 54, 41, 42, 43, 44, 45, 68, 36, 35, 31, 30, 28};
int c2[] = {1, 2, 3, 4, 5, 6, 7, 8, 9};
int b3[] = {1, 28, 30, 29, 33, 32, 72, 59, 60, 61, 62, 63, 50, 18, 17, 13, 12, 10};
int c3[] = {19, 20, 21, 22, 23, 24, 25, 26, 27};
int b4[] = {28, 19, 21, 20, 24, 23, 63, 50, 51, 52, 53, 54, 41, 9, 8, 4, 3, 1};
int c4[] = {10, 11, 12, 13, 14, 15, 16, 17, 18};
//////////aaaa
int b5[] = {37, 46, 48, 47, 51, 50, 18, 23, 24, 25, 26, 27, 32, 72, 71, 67, 66, 64};
int c5[] = {55, 56, 57, 58, 59, 60, 61, 62, 63};
int b6[] = {45, 68, 69, 70, 71, 72, 59, 27, 26, 22, 21, 19, 10, 1, 3, 2, 6, 5};
int c6[] = {36, 31, 35, 34, 28, 30, 29, 33, 32};
int b7[] = {36, 5, 6, 7, 8, 9, 14, 54, 53, 49, 48, 46, 55, 64, 66, 65, 69, 68};
int c7[] = {45, 40, 44, 43, 37, 39, 38, 42, 41};
int b8[] = {5, 45, 44, 40, 39, 37, 46, 55, 57, 56, 60, 59, 27, 32, 33, 34, 35, 36};
int c8[] = {68, 70, 69, 65, 72, 71, 67, 66, 64};
///=======================
///******** 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
int d1[] = {13, 17, 16, 52, 53, 49, 38, 39, 40, 65, 69, 70, 34, 33, 29, 22, 21, 20};
int d2[] = {13, 12, 11, 4, 8, 7, 43, 44, 40, 65, 66, 67, 56, 60, 61, 25, 24, 20};
int d3[] = {58, 62, 61, 25, 26, 22, 29, 30, 31, 2, 6, 7, 43, 42, 38, 49, 48, 47};
int d4[] = {2, 3, 4, 11, 15, 16, 52, 51, 47, 58, 57, 56, 67, 71, 70, 34, 35, 31};
void r1(){ rotate2(d1, 0);}
void r2(){rotate2(d1, 1);}
void r3(){rotate2(d2, 0);}
void r4(){rotate2(d2, 1);}
void r21(){rotate2(d3, 0);}
void r22(){rotate2(d3, 1);}
void r23(){rotate2(d4, 0);}
void r24(){rotate2(d4, 1);}
void r5(){rotate1(b1, c1);}
void r6(){rotate1(b1, c1);rotate1(b1, c1);}
void r7(){rotate1(b2, c2);}
void r8(){rotate1(b2, c2);rotate1(b2, c2);}
void r9(){rotate1(b3, c3);}
void r10(){rotate1(b3, c3);rotate1(b3, c3);}
void r11(){rotate1(b4, c4);}
void r12(){rotate1(b4, c4);rotate1(b4, c4);}
void r13(){rotate1(b5, c5);}
void r14(){rotate1(b5, c5); rotate1(b5, c5);}
void r15(){rotate1(b6, c6);}
void r16(){rotate1(b6, c6); rotate1(b6, c6);}
void r17(){rotate1(b7, c7);}
void r18(){rotate1(b7, c7); rotate1(b7, c7);}
void r19(){rotate1(b8, c8);}
void r20(){rotate1(b8, c8); rotate1(b8, c8);}
///=========================================
bool dfs(int d){
if (d > 3) return false;
if (check()) return true;
///*******************
r1();
if (dfs(d+1)) return true;
r2();
///*******************
///*******************
r2();
if (dfs(d+1)) return true;
r1();
///*******************
///*******************
r3();
if (dfs(d+1)) return true;
r4();
///*******************
///*******************
r4();
if (dfs(d+1)) return true;
r3();
///*******************
///*******************
r5();
if (dfs(d+1)) return true;
r6();
///*******************
///*******************
r6();
if (dfs(d+1)) return true;
r5();
///*******************
///*******************
r7();
if (dfs(d+1)) return true;
r8();
///*******************
///*******************
r8();
if (dfs(d+1)) return true;
r7();
///*******************
///*******************
r9();
if (dfs(d+1)) return true;
r10();
///*******************
///*******************
r10();
if (dfs(d+1)) return true;
r9();
///*******************
///*******************
r11();
if (dfs(d+1)) return true;
r12();
///*******************
///*******************
r12();
if (dfs(d+1)) return true;
r11();
///*******************
///*******************
r13();
if (dfs(d+1)) return true;
r14();
///*******************
///*******************
r14();
if (dfs(d+1)) return true;
r13();
///*******************
///*******************
r15();
if (dfs(d+1)) return true;
r16();
///*******************
///*******************
r16();
if (dfs(d+1)) return true;
r15();
///*******************
///*******************
r17();
if (dfs(d+1)) return true;
r18();
///*******************
///*******************
r18();
if (dfs(d+1)) return true;
r17();
///*******************
///*******************
r19();
if (dfs(d+1)) return true;
r20();
///*******************
///*******************
r20();
if (dfs(d+1)) return true;
r19();
///*******************
///*******************
r21();
if (dfs(d+1)) return true;
r22();
///*******************
///*******************
r22();
if (dfs(d+1)) return true;
r21();
///*******************
///*******************
r23();
if (dfs(d+1)) return true;
r24();
///*******************
///*******************
r24();
if (dfs(d+1)) return true;
r23();
///*******************
return false;
}
int main(){
int T;
scanf("%d",&T);
while(T--){
int cnt = 0;
for (int i = 0; i < 8; ++i){
for (int j = 0; j < 9; ++j){
int x;
scanf("%d",&x);
a[++cnt] = x;
}
}
int ans = dfs(0);
if (ans){
puts("YES");
}
else puts("NO");
}
return 0;
}
cube cube cube
Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 327680/327680 K (Java/Others)Total Submission(s): 9313 Accepted Submission(s): 127
Rubik's cube is shown in the following picture:

The plane expansion of the Rubik's cube is shown in the following figure, each number represents the color corresponding to each cube.
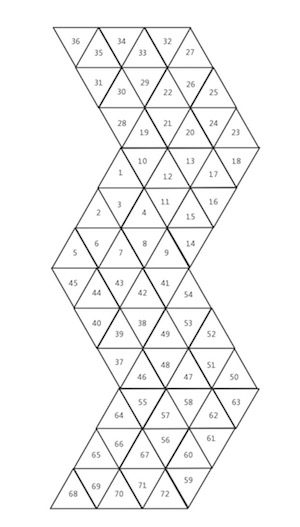
The following picture explains how to rotate this strange cube. If you still feel confused, you can refer to
http://www.bilibili.com/video/av8452301/?from=search&seid=11750270100959783079 .
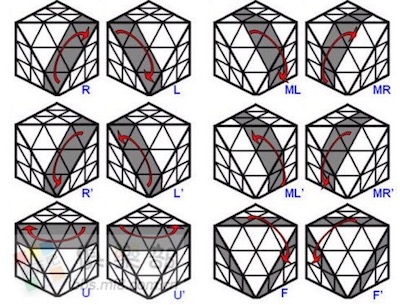
Each test case consists of 72 integers which correspond to the colors of each location of the Rubik's Cube. Each number represents one color, it's guaranteed that there are exactly 8 colors and each color appears 9 times.
1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5 6 6 6 6 6 6 6 6 6 7 7 7 7 7 7 7 7 7 8 8 8 8 8 8 8 8 8
YES
Statistic | Submit | Discuss | Note