Title:

M Fibonacci sequence F[n] is an integer sequence, which is defined as follows:

F[0] = a 
F[1] = b 
F[n] = F[n-1] * F[n-2] ( n > 1 ) 

Now given a, b, n, can you find the value of F[n]?

Input

The input contains multiple sets of test data
Each group of data takes up one row, including three integers a, b, n (0 < = a, b, n < = 10 ^ 9)

Output

For each group of test data, please output an integer F[n]. Because F[n] may be very large, you only need to output the value of F[n] after taking the module of 100000007, and each group of data output a row.

Sample Input

0 1 0
6 10 2

Sample Output

0
60

Idea: this problem uses Fermat's small theorem {if p is prime number and gcd(a,p)=1, then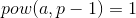(mod p)}, so I've been stuck for a long time,,,

set up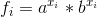, easy to launch.

be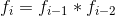

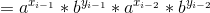
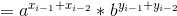
It can be seen that the index of a and B is Fibonacci series. When I do it, the index is mod 1 e 9 + 7.. Silly. Using Fermat's theorem, we can see that every 1e9+6 index will become 1, so the index is mod 1e9+6

After we get the exponent of ab, we can get the fast power

Code:

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define maxn 10
#define mod 1000000007

///Matrix of n rows and m columns
struct AA
{
    ll n,m,a[maxn][maxn];
    void mem1()
    {
        memset(a,0,sizeof(a));///When n=m, initialize to unit matrix
        for(int i=0;i<n;i++)
            a[i][i]=1;
    }
};

///aa matrix of n rows and m columns * bb matrix of M rows and k columns
AA mul(AA aa,AA bb,int n,int m,int kk)
{
    AA cc;
    cc.n=cc.m=2;
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<kk;j++)
        {
            int x=0;
            for(int k=0;k<m;k++)
            {
                x+=(aa.a[i][k]*bb.a[k][j])%(mod-1);
                x%=(mod-1);
            }
            cc.a[i][j]=x;
        }
    }
    return cc;
}

///The m-power of the matrix aa
AA POW(AA aa,ll m)
{
    AA d;d.n=d.m=2;
    d.mem1();
    while(m)
    {
        if(m&1)
        {
            d=mul(d,aa,2,2,2);
        }
        m/=2;
        aa=mul(aa,aa,2,2,2);
    }
    return d;
}
ll pp(ll i,ll j)
{
    ll zz=1;
    while(j)
    {
        if(j&1) {zz*=i;zz%=mod;}
        j/=2;
        i*=i;
        i%=mod;
    }
    return zz;
}
ll n,a,b,x,y;
int main()
{
    while(~scanf("%lld%lld%lld",&a,&b,&n))
    {
        if(n==0)
        {
            printf("%lld\n",a%mod);
        }
        else if(n==1)
        {
            printf("%lld\n",b%mod);
        }
        else
        {
            AA aa,bb;aa.n=aa.m=2;
            aa.a[0][0]=1;aa.a[0][1]=1;
            aa.a[1][0]=1;aa.a[1][1]=0;
            AA cc=POW(aa,n-1);
            bb.a[0][0]=1;
            bb.a[1][0]=0;
            cc=mul(cc,bb,2,2,1);
            printf("%lld\n",(pp(a,cc.a[1][0])*pp(b,cc.a[0][0]))%mod);
        }
    }
}