Topic link:
Main idea of the title:
Given the number of points in a tree, "u, v" means that V is the father of U.
m operations:
"Txy" means that all the sub-trees rooted in x are dyed with the color y.
"Cx" means asking what color is the node x?
Multiple groups (T < 10)
Data range:
n,m≤500001≤x≤n,1≤y≤109
Ideas for problem solving:
Routine questions, get the DFS sequence, and then use the segment tree segment updates, as well as a single point query on the over!
Foreign language:
Learned how to do DFS sequence, I know two methods at present:
One is to directly record the start and end timestamps of each node, which is to label the nodes in the order of DFS, such as this (example): 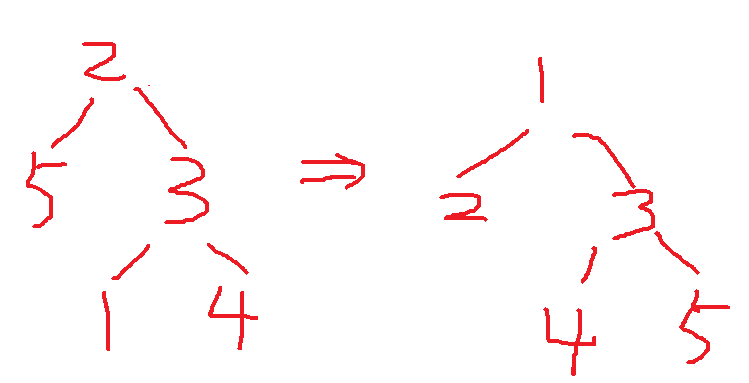
Operating node 3 is equivalent to modifying interval [3, 5].
Another is to remember the time stamp at which each node starts and the size of the subtree rooted on that node.
The two methods are similar, the ultimate goal is to correspond the tree to the interval, transform the operation of the tree into the modification of the interval, and use the line segment tree to solve the problem.
See the code for details:
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <set>
#include <map>
#include <queue>
using namespace std;
typedef long long LL;
const int inf = 1 << 30;
const LL INF = 1LL << 60;
const int MaxN = 50005;
int T;
int n, m;
int all, time, cas;
int pre[2 * MaxN + 5], last[MaxN + 5], other[2 * MaxN + 5];
int fa[MaxN + 5];
int left[MaxN + 5], right[MaxN + 5];
struct segtree
{
int l, r;
int task; //The color of the current interval
}tree[4 * MaxN + 5];
int lazy[4 * MaxN + 5];//lazy[rt] denotes the color of the interval governed by the RT node
//It feels a little redundant, as if it could be achieved with that task, but it's not written correctly.
void build(int x, int y) { //Build up trees
pre[++all] = last[x];
last[x] = all;
other[all] = y;
}
int find(int x) { //Find the root node of the tree
int father = fa[x];
while(x != father) {
x = father;
father = fa[father];
}
return x;
}
void Dfs(int x, int fa) {
int ed = last[x], dr;
++time;
left[x] = time; //Start time, corresponding to the left end of the interval
while(ed != -1) {
dr = other[ed];
if(dr != fa)
Dfs(dr, x);
ed = pre[ed];
}
right[x] = time; //The end time corresponds to the right end of the interval
}
void Build(int rt, int l, int r) //Line segment tree
{
tree[rt].l = l, tree[rt].r = r;
tree[rt].task = -1; //Initialized to -1
lazy[rt] = -1;
if(l == r) return ;
int mid = (l + r) >> 1;
Build(rt << 1, l, mid);
Build(rt << 1 | 1, mid + 1, r);
}
void push_down(int rt) { //Decentralization mark
if(lazy[rt] != -1) {
tree[rt << 1].task = lazy[rt];
tree[rt << 1 | 1].task = lazy[rt];
lazy[rt << 1] = lazy[rt];
lazy[rt << 1 | 1] = lazy[rt];
lazy[rt] = -1;
}
}
void update(int rt, int L, int R, int t)
{
if(L <= tree[rt].l && tree[rt].r <= R) {
lazy[rt] = t; //Interval modification
tree[rt].task = t;
return;
}
push_down(rt);
int mid = (tree[rt].l + tree[rt].r) >> 1;
if(L <= mid) update(rt << 1, L, R, t);
if(R > mid) update(rt << 1 | 1, L, R, t);
}
int query(int rt, int pos) {
if(tree[rt].l == pos && pos == tree[rt].r) {
return tree[rt].task;
}
push_down(rt);
int mid = (tree[rt].l + tree[rt].r) >> 1;
if(pos <= mid) return query(rt << 1, pos);
else return query(rt << 1 | 1, pos);
}
int main()
{
cas = 0;
scanf("%d", &T);
while(T--) {
time = 0;
all = -1; memset(last, -1, sizeof(last));
scanf("%d", &n);
for(int i = 1; i <= n; i++) fa[i] = i;
for(int i = 1; i <= n - 1; i++) {
int u, v;
scanf("%d %d", &u, &v);
fa[u] = v;
build(v, u);
}
int root = find(1);//You can find any point in 1~n.
//printf("root = %d\n", root);
Dfs(root, 0);
Build(1, 1, time);
printf("Case #%d:\n", ++cas);
scanf("%d", &m);
for(int i = 1; i <= m; i++) {
char op;
int x, y;
scanf(" %c", &op);
if(op == 'C') {
scanf("%d", &x);
printf("%d\n", query(1, left[x]));//Single point query
}
else if(op == 'T') {
scanf("%d %d", &x, &y);
update(1, left[x], right[x], y);//Renewal interval
}
}
memset(tree, 0, sizeof(tree));
memset(left, 0, sizeof(left));
memset(right, 0, sizeof(right));
memset(pre, 0, sizeof(pre));
memset(other, 0, sizeof(other));
}
return 0;
}
The start timestamp and the subtree size are much the same, and they are pasted together:
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <set>
#include <map>
#include <queue>
using namespace std;
typedef long long LL;
const int inf = 1 << 30;
const LL INF = 1LL << 60;
const int MaxN = 50005;
int T;
int n, m;
int all, time, cas;
int pre[2 * MaxN + 5], last[MaxN + 5], other[2 * MaxN + 5];
int fa[MaxN + 5];
int start[MaxN + 5], size[MaxN + 5];
struct segtree
{
int l, r;
int task;
}tree[4 * MaxN + 5];
int lazy[4 * MaxN + 5];
void build(int x, int y) {
pre[++all] = last[x];
last[x] = all;
other[all] = y;
}
int find(int x) {
int father = fa[x];
while(x != father) {
x = father;
father = fa[father];
}
return x;
}
void Dfs(int x, int fa) {
int ed = last[x], dr;
++time;
start[x] = time;
while(ed != -1) {
dr = other[ed];
if(dr != fa) {
Dfs(dr, x);
size[x] += size[dr];
}
ed = pre[ed];
}
}
void Build(int rt, int l, int r)
{
tree[rt].l = l, tree[rt].r = r;
tree[rt].task = -1;
lazy[rt] = -1;
if(l == r) return ;
int mid = (l + r) >> 1;
Build(rt << 1, l, mid);
Build(rt << 1 | 1, mid + 1, r);
}
void push_down(int rt) {
if(lazy[rt] != -1) {
tree[rt << 1].task = lazy[rt];
tree[rt << 1 | 1].task = lazy[rt];
lazy[rt << 1] = lazy[rt];
lazy[rt << 1 | 1] = lazy[rt];
lazy[rt] = -1;
}
}
void update(int rt, int L, int R, int t)
{
if(L <= tree[rt].l && tree[rt].r <= R) {
lazy[rt] = t;
tree[rt].task = t;
return;
}
push_down(rt);
int mid = (tree[rt].l + tree[rt].r) >> 1;
if(L <= mid) update(rt << 1, L, R, t);
if(R > mid) update(rt << 1 | 1, L, R, t);
}
int query(int rt, int pos) {
if(tree[rt].l == pos && pos == tree[rt].r) {
return tree[rt].task;
}
push_down(rt);
int mid = (tree[rt].l + tree[rt].r) >> 1;
if(pos <= mid) return query(rt << 1, pos);
else return query(rt << 1 | 1, pos);
}
int main()
{
cas = 0;
scanf("%d", &T);
while(T--) {
time = 0;
all = -1; memset(last, -1, sizeof(last));
scanf("%d", &n);
for(int i = 1; i <= n; i++) fa[i] = i, size[i] = 1;
for(int i = 1; i <= n - 1; i++) {
int u, v;
scanf("%d %d", &u, &v);
fa[u] = v;
build(v, u);
}
int root = find(1);
//printf("root = %d\n", root);
Dfs(root, 0);
Build(1, 1, time);
printf("Case #%d:\n", ++cas);
scanf("%d", &m);
for(int i = 1; i <= m; i++) {
char op;
int x, y;
scanf(" %c", &op);
if(op == 'C') {
scanf("%d", &x);
printf("%d\n", query(1, start[x]));
}
else if(op == 'T') {
scanf("%d %d", &x, &y);
update(1, start[x], start[x] + size[x] - 1, y);
}
}
memset(tree, 0, sizeof(tree));
memset(start, 0, sizeof(start));
memset(size, 0, sizeof(size));
memset(pre, 0, sizeof(pre));
memset(other, 0, sizeof(other));
}
return 0;
}