~by Wjvje 2019-5-3
Title Link: http://acm.hdu.edu.cn/showproblem.php?pid=1255
Title Description:
Area covered by
Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 8647 Accepted Submission(s): 4333
Problem Description
Given some rectangles on a plane, the area of the area covered by these rectangles at least twice is obtained
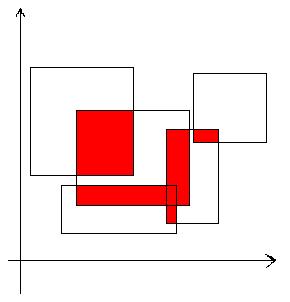
Input
The first row of input data is a positive integer t (1 < = T < = 100), which represents the number of test data. The first row of each test data is a positive integer N (1 < = N < = 1000), which represents the number of rectangles, and then N rows of data. Each row contains four floating-point numbers, representing the coordinates of the upper left corner and the lower right corner of a rectangle on the plane. The upper and lower sides of the rectangle are parallel to the X-axis, and the left and right sides are parallel to the Y-axis Range from 0 to 100000
Note: there are many input data in this question. It is recommended to use scanf to read in data
Output
For each group of test data, calculate the area covered by these rectangles at least twice. Keep two decimal places for the result
Sample Input
2 5 1 1 4 2 1 3 3 7 2 1.5 5 4.5 3.5 1.25 7.5 4 6 3 10 7 3 0 0 1 1 1 0 2 1 2 0 3 1
Sample Output
Core topic:
The area of the intersection of rectangles.
Thought analysis:
Principle bougie Island, rectangular Union Function sum
Function sum![Len2[1]](/images/article/8aef162ed5cde850ff2c40b2b11dc68b.jpg) Yes.
Yes.
Code implementation: (changed two places Len2 and pushUp)
#include<bits/stdc++.h>
#define io ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using namespace std;
const int N=2e5+100;//-----------Note 4*N
using namespace std;
struct Node
{
double l,r,h;
int value;
}a[N];
bool cmp(Node aa,Node bb)
{
return aa.h<bb.h;
}
//bool cmp2(double aa,double bb) / these things are not easy to use at all
//{
// return bb-aa>=1e-9;
//}
int Left[N],Right[N],dat[N];//Left son node, right son node
double Len2[N];
double xx[N],Len[N];//Length covered in the interval contained by each node, double type
void build(int p,int l,int r)
{
Left[p]=l;
Right[p]=r;//This place always likes to be written as 2*p, 2*p+1;
if(l==r)
{
dat[p]=0;
return ;
}
int mid=(l+r)/2;
build(p*2,l,mid);
build(p*2+1,mid+1,r);
dat[p]=0;
}
void pushUp(int p)//-----------The core of interval intersection
{
//The interval can also be completely covered
if(dat[p]>1)
Len[p]=Len2[p]=xx[Right[p]+1]-xx[Left[p]];
//cout<<p<<":"<<xx[Right[p]+1]<<"==="<<xx[Left[p]]<<" "<<Len[p]<<endl;
else if(dat[p]==1)
{
Len[p]=xx[Right[p]+1]-xx[Left[p]];
if(Right[p]==Left[p])Len2[p]=0;
else Len2[p]=Len[2*p]+Len[2*p+1];
}
else
{
if(Right[p]==Left[p])Len[p]=Len2[p]=0;
else
{
Len[p]=Len[2*p]+Len[2*p+1];
Len2[p]=Len2[2*p]+Len2[2*p+1];
}
}
//cout<<p<<":"<<Len[2*p]<<"+"<<Len[2*p+1]<<" "<<" "<<2*p<<endl;
//dat==0, that is, it is not completely covered, then the length of which is covered is determined by the child node
}
void change(int p,int l,int r,int v)
{
if(l<=Left[p]&&r>=Right[p])
{
dat[p]+=v;//The number of times this point (multiple intervals) is covered, completely covered, + = v
pushUp(p); //The number of times of being covered changes and renews the Len of oneself and ancestors;
return ;
}
int mid=(Left[p]+Right[p])/2;
if(l<=mid)change(p*2,l,r,v);
if(r>mid)change(p*2+1,l,r,v);
pushUp(p);//Two changes cause the number of times that the child nodes are covered to change, updating Len of p;
}
int main()
{
io;
int n;
int cas=0;
int t;
cin>>t;
while(t--)
{
cin>>n;
int tot=0;
int cnt=0;
memset(Len,0,sizeof(Len));//------guan jian**
memset(xx,0,sizeof(xx));
memset(Left,0,sizeof(Left));
memset(Right,0,sizeof(Right));
memset(dat,0,sizeof(dat));
double sum_s=0;
for(int i=1;i<=n;++i)
{
double x1,y1,x2,y2;
cin>>x1>>y1>>x2>>y2;//-----Pay attention to which two corners
//cout<<"("<<x2<<"-"<<x1<<")*("<<y2<<"-"<<y1<<")=="<<abs(x2-x1)*abs(y2-y1)<<endl;
a[++tot].l=x1;
a[tot].r=x2;
a[tot].h=y1;
a[tot].value=1;
//cout<<"tot="<<tot<<",,,,,"<<a[tot].h<<endl;
a[++tot].l=x1;
a[tot].r=x2;
a[tot].h=y2;
a[tot].value=-1;
//cout<<"tot="<<tot<<",,,,,, "<<a[tot].h<<endl;
xx[++cnt]=x1;
xx[++cnt]=x2;
}
sort(xx+1,xx+1+cnt);
cnt=unique(xx+1,xx+1+cnt)-xx-1;//---------(-xx-1);
// for(int i=1;i<=cnt;++i)cout<<xx[i]<<" ? ";
// cout<<endl;
build(1,1,cnt-1);//--------Each leaf node in the line segment tree represents the cells whose left boundary is this point, so:cnt-1
sort(a+1,a+1+tot,cmp);
//cout<<a[10].h<<"??????????????"<<endl;
double ans=0;
for(int i=1;i<=tot;++i) //When i==tot, Len [1] = = 0. It is OK to remove tot
{
//cout<<a[i].h<<"-- "<<a[i].l<<" --"<<a[i].r<<endl;
int x=lower_bound(xx+1,xx+1+cnt,a[i].l)-xx;
int y=lower_bound(xx+1,xx+1+cnt,a[i].r)-xx;//cout<<i<<endl;
//cout<<x<<";;;;;;;"<<y<<" /"<<a[i].r<<endl;
change(1,x,y-1,a[i].value);
ans+=(double)Len2[1]*(a[i+1].h-a[i].h);/////----------------------Len2
// cout<<"length_total: "<<Len[1]<<" distance: "<<
// "("<<a[i+1].h<<"-"<<a[i].h<<") =="<<(a[i+1].h-a[i].h)<<endl;
}
cout<<fixed<<setprecision(2)<<ans<<endl;//cout precision control, learn
}
return 0;
}
The end;