This article is reproduced from: Implementation of HashMap in Jdk1.7 and 1.8
Essential for interview: Principles and differences of HashMap, Hashtable and ConcurrentHashMap

1, A glimpse of HashMap

HashMap is a more widely used hash table implementation, and in most cases, it can carry out put and get operations under the condition of constant time performance. To master HashMap, you should mainly grasp it from the following points:

• The bottom layer of jdk1.7 is realized by array (also called "bit bucket") and linked list; The bottom layer of jdk1.8 is implemented by array + linked list / red black tree
• Null keys and null values can be stored, and threads are not safe. In HashMap, null can be used as a key. There is only one such key, but the value corresponding to one or more keys can be null. When the get() method returns a null value, it can mean that the key does not exist in the HashMap or that the value corresponding to the key is null. Therefore, in the HashMap, the get() method cannot be used to judge whether there is a key in the HashMap, but the containsKey() method should be used to judge. In Hashtable, neither key nor value can be null.
• The initial size is 16, the capacity expansion is: newsize = oldsize*2, and the size must be the n-th power of 2
• For the entire Map, the storage location of the elements in the original array will be recalculated and reinserted each time
• Judge whether to expand the capacity after inserting the element, which may be invalid (if the element is expanded after insertion, if it is not inserted again, it will produce invalid expansion)
• When the total number of elements in the Map exceeds 75% of the Entry array, the capacity expansion operation is triggered. In order to reduce the length of the linked list, the elements are distributed more evenly
• In 1.7, the capacity is expanded first and then the new value is inserted, and in 1.8, the capacity is interpolated first and then expanded

Why is HashMap thread unsafe?
When approaching the critical point, if two or more threads put at this time, they will both resize and reHash (recalculate the location of the key), and reHash may form a linked list link in the case of concurrency. To sum up, in a multithreaded environment, using HashMap for put operation will cause an endless loop, resulting in CPU utilization close to 100%. Therefore, HashMap cannot be used in concurrency. Why do put operations performed concurrently cause an endless loop? This is because multithreading will cause the Entry linked list of HashMap to form a ring data structure. Once the ring data structure is formed, the next node of the Entry will never be empty, and an endless loop will be generated to obtain the Entry. In the case of jdk1.7, it is easy to form linked list links during concurrent capacity expansion. This situation is much better in 1.8. Because in 1.8, when the length of the linked list is greater than the threshold (the default length is 8), the linked list will be changed into a tree (red black tree) structure.

2, Implementation of HashMap in jdk1.7

The underlying maintenance of HashMap is array + linked list. We can see it through a short source code:

 /**
  * The default initial capacity - MUST be a power of two.
  *  The default initial size is 16
  */
 static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16

 /**
  * The maximum capacity, used if a higher value is implicitly specified
  * by either of the constructors with arguments.
  * MUST be a power of two <= 1<<30.
  *  That is, the maximum capacity must be 2 ^ 30
  */
 static final int MAXIMUM_CAPACITY = 1 << 30;

 /**
  * The load factor used when none specified in constructor.
  * The load factor is 0.75
  */
 static final float DEFAULT_LOAD_FACTOR = 0.75f;

 /**
  * The bin count threshold for using a tree rather than list for a
  * bin.  Bins are converted to trees when adding an element to a
  * bin with at least this many nodes. The value must be greater
  * than 2 and should be at least 8 to mesh with assumptions in
  * tree removal about conversion back to plain bins upon
  * shrinkage.
  * Roughly speaking, hash conflicts are stored in a single linked list by default. When the number of single linked list nodes is greater than 8, they will be converted to red black tree storage
  */
 static final int TREEIFY_THRESHOLD = 8;

 /**
  * The bin count threshold for untreeifying a (split) bin during a
  * resize operation. Should be less than TREEIFY_THRESHOLD, and at
  * most 6 to mesh with shrinkage detection under removal.
  * hash Conflicts are stored in a single linked list by default. When the number of single linked list nodes is greater than 8, they will be converted 
     Store for red black tree.
* When the number of nodes in the red black tree is less than 6, it is converted to single linked list storage
  */
 static final int UNTREEIFY_THRESHOLD = 6;

 /**
  * The smallest table capacity for which bins may be treeified.
  * (Otherwise the table is resized if too many nodes in a bin.)
  * Should be at least 4 * TREEIFY_THRESHOLD to avoid conflicts
  * between resizing and treeification thresholds.
  * hash Conflicts are stored in single linked list by default. When the number of single linked list nodes is greater than 8, they will be converted to red black tree storage.
  * However, there is a premise: the array length is required to be greater than 64, otherwise it will not be converted
  */
 static final int MIN_TREEIFY_CAPACITY = 64;

From the above code, you can see the initial capacity (16), load factor and description of the array. Each element in the array is actually an entry < K, V > [] table, and the key and value in the Map are stored in the form of an entry. Entry contains four attributes: key, value, hash value and next for one-way linked list. For the specific definition of entry < K, V >, see the following source code:

static class Entry<K,V> implements Map.Entry<K,V> {
    final K key;
    V value;
    Entry<K,V> next;
    int hash;
 
    Entry(int h, K k, V v, Entry<K,V> n) {
        value = v;
        next = n;
        key = k;
        hash = h;
    }
 
    public final K getKey() {
        return key;
    }
 
    public final V getValue() {
        return value;
    }
 
    public final V setValue(V newValue) {
        V oldValue = value;
        value = newValue;
        return oldValue;
    }
 
    public final boolean equals(Object o) {
        if (!(o instanceof Map.Entry))
            return false;
        Map.Entry e = (Map.Entry)o;
        Object k1 = getKey();
        Object k2 = e.getKey();
        if (k1 == k2 || (k1 != null && k1.equals(k2))) {
            Object v1 = getValue();
            Object v2 = e.getValue();
            if (v1 == v2 || (v1 != null && v1.equals(v2)))
                return true;
        }
        return false;
    }
 
    public final int hashCode() {
        return Objects.hashCode(getKey()) ^ Objects.hashCode(getValue());
    }
 
    public final String toString() {
        return getKey() + "=" + getValue();
    }
 
    /**
     * This method is invoked whenever the value in an entry is
     * overwritten by an invocation of put(k,v) for a key k that's already
     * in the HashMap.
     */
    void recordAccess(HashMap<K,V> m) {
    }
 
    /**
     * This method is invoked whenever the entry is
     * removed from the table.
     */
    void recordRemoval(HashMap<K,V> m) {
    }
}

The initial value of HashMap should consider the loading factor:

• Hash conflict: after the hash values of several keys are modular according to the size of the array, if they fall on the same array subscript, they will form an Entry chain. To find the Key, you need to traverse each element on the Entry chain and perform equals() comparison.
• Load factor: in order to reduce the probability of hash conflict, by default, when the key value pairs in HashMap reach 75% of the array size, capacity expansion will be triggered. Therefore, if the estimated capacity is 100, it is necessary to set the array size of 100 / 0.75 = 134.
• Space for time: if you want to speed up the Key search time, you can further reduce the loading factor and increase the initial size to reduce the probability of hash conflict.

HashMap and Hashtable use the hash algorithm to determine the storage of their elements. Therefore, the hash tables of HashMap and Hashtable contain the following attributes:

• capacity: the number of buckets in the hash table
• Initial capacity: the number of buckets when creating a hash table. HashMap allows you to specify the initial capacity in the constructor
• size: the number of records in the current hash table
• Load factor: the load factor is equal to "size/capacity". A load factor of 0 indicates an empty hash table, 0.5 indicates a half full hash table, and so on. The lightly loaded hash table has the characteristics of less conflicts and is suitable for insertion and query (but it is slow to iterate elements with Iterator)

In addition, there is a "load limit" in the hash table. The "load limit" is a value of 0 ~ 1. The "load limit" determines the maximum filling degree of the hash table. When the load factor in the hash table reaches the specified "load limit", the hash table will automatically double the capacity (the number of buckets), and reallocate the original objects into new buckets, which is called rehashing.

The constructors of HashMap and Hashtable allow you to specify a load limit. The default "load limit" of HashMap and Hashtable is 0.75, which indicates that rehashing will occur when 3 / 4 of the hash table has been filled.

The default value for load limit (0.75) is a compromise between time and space costs:

• A higher "load limit" can reduce the memory space occupied by the hash table, but it will increase the time overhead of querying data, and query is the most frequent operation (both get() and put() methods of HashMap use query)
• A lower "load limit" will improve the performance of query data, but will increase the memory overhead occupied by hash tables
  The program can adjust the "load limit" value according to the actual situation. (the load limit and load factor I understand are actually the same value, that is, rehash occurs when the load factor reaches 0.75)

When a pair of key values are put into the HashMap, it will calculate a position according to the hashCode value of the key, which is the position where the object is to be stored in the array. Refer to the following code for the calculation process:

transient int hashSeed = 0;
final int hash(Object k) {
     int h = hashSeed;
     if (0 != h && k instanceof String) {
         return sun.misc.Hashing.stringHash32((String) k);
     }
 
     h ^= k.hashCode();
 
     // This function ensures that hashCodes that differ only by
     // constant multiples at each bit position have a bounded
     // number of collisions (approximately 8 at default load factor).
     h ^= (h >>> 20) ^ (h >>> 12);
     return h ^ (h >>> 7) ^ (h >>> 4);
 }
 
 /**
  * Returns index for hash code h.
  */
 static int indexFor(int h, int length) {
     // assert Integer.bitCount(length) == 1 : "length must be a non-zero power of 2";
     return h & (length-1);
 }

The value calculated by hash will use the indexFor method to find the table subscript where it should be located. When two key s are the same through hashCode calculation, A hash conflict (collision) occurs. HashMap uses A linked list (zipper method) to solve the hash conflict. In case of hash conflict, set the Entry stored in the array as the next of the new value (note here that, for example, both A and B are mapped to the subscript i after hashing, and there has been A before. When map.put(B), put B into the subscript i, and A is the next of B, so the new value is stored in the array, and the old value is on the linked list of the new value). That is, the new value is used as the head node of this linked list. Why do you want to do this? It is said that the later inserted Entry is more likely to be found (because the whole linked list will be traversed during get query). It needs to be studied here. If any great God knows, please leave A message. There is A saying that the linked list has high search complexity and high insertion and deletion performance. If the new value is inserted at the end, it needs to go through A round of traversal first. This time complexity is high and the overhead is large. If it is inserted at the head node, it saves the traversal overhead and gives play to the advantage of high insertion performance of the linked list.

If there is no object in the position, the object is directly put into the array; If an object already exists in this position, start searching along the chain of the existing object (in order to judge whether the values are the same, map does not allow duplicate < key, value > key value pairs). If there are objects in this chain, use the equals method for comparison. If the equals method comparison of each object in this chain is false, put the object into the array, Then link the pre-existing object in the array to the back of this object.

Add node to the linked list: after finding the array subscript, the key will be re judged first. If there is no repetition, the new value will be put into the header of the linked list.

void addEntry(int hash, K key, V value, int bucketIndex) {
    // If the current HashMap size has reached the threshold and there are already elements in the array position where the new value is to be inserted, the capacity should be expanded
    if ((size >= threshold) && (null != table[bucketIndex])) {
        // Capacity expansion
        resize(2 * table.length);
        // After capacity expansion, recalculate the hash value
        hash = (null != key) ? hash(key) : 0;
        // Recalculate the new subscript after capacity expansion
        bucketIndex = indexFor(hash, table.length);
    }
    // Look down
    createEntry(hash, key, value, bucketIndex);
}
// This is very simple. In fact, it is to put the new value into the header of the linked list, and then size++
void createEntry(int hash, K key, V value, int bucketIndex) {
    Entry<K,V> e = table[bucketIndex];
    table[bucketIndex] = new Entry<>(hash, key, value, e);
    size++;
}

The main logic of this method is to first judge whether capacity expansion is needed. If it is necessary, expand the capacity first, and then insert the new data into the header of the linked list at the corresponding position of the expanded array.

Capacity expansion is to replace the original small array with a new large array, and migrate the values in the original array to the new array. Due to the double expansion, all nodes of the linked list in the original table[i] will be split into newTable[i] and newTable[i+oldLength] positions of the new array during the migration process. If the length of the original array is 16, all elements in the linked list at the original table[0] will be allocated to newTable[0] and newTable[16] in the new array after capacity expansion. During capacity expansion, a new empty array will be created and filled with old items. Therefore, in this filling process, if a thread obtains a value, it is likely to get a null value instead of the original value we want.

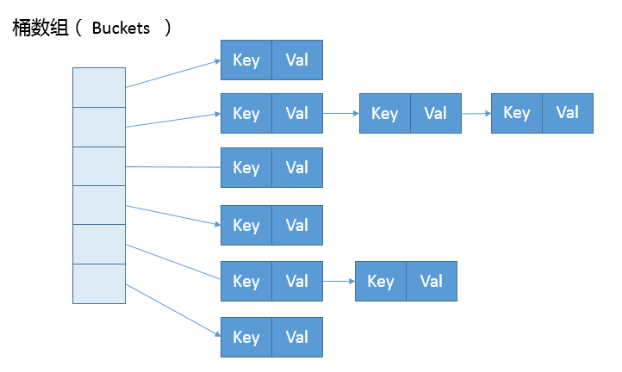
In the figure, the left part represents the hash table, also known as the hash array (the default array size is 16, and each pair of key value pairs actually exists in the internal class entry of the map). Each element of the array is the head node of a single linked list, followed by a blue linked list to resolve conflicts. If different keys are mapped to the same position of the array, Put it into the single linked list.

As mentioned earlier, the key of HashMap is allowed to be null. When this happens, it will be placed in table[0].

private V putForNullKey(V value) {
    for (Entry<K,V> e = table[0]; e != null; e = e.next) {
        if (e.key == null) {
            V oldValue = e.value;
            e.value = value;
            e.recordAccess(this);
            return oldValue;
        }
    }
    modCount++;
    addEntry(0, null, value, 0);
    return null;
}

Capacity expansion occurs when size > = threshold (threshold is equal to "capacity * load factor").

void addEntry(int hash, K key, V value, int bucketIndex) {
    if ((size >= threshold) && (null != table[bucketIndex])) {
        resize(2 * table.length);
        hash = (null != key) ? hash(key) : 0;
        bucketIndex = indexFor(hash, table.length);
    }
 
    createEntry(hash, key, value, bucketIndex);
}

Special note: * * in jdk1.7, resize occurs only when size > = threshold and there is an Entry in the slot in the table** That is, it is possible that although size > = threshold, the capacity will not be expanded until there is at least one Entry in the corresponding slot. You can see from the above code that each resize will double the capacity (2 * table.length).

3, Implementation of HashMap in jdk1.8

In jdk1.8, the internal structure of HashMap can be regarded as a composite structure of an array (node < K, V > [] table) and a linked list. The array is divided into bucket s. The addressing of key value pairs in the array is determined by the hash value (key value pairs with the same hash value are stored in the form of a linked list. It should be noted that if the size of the linked list exceeds the threshold (tree_threshold, 8) , the linked list in the figure will be transformed into a tree (red black tree) structure.

transient Node<K,V>[] table;

The name of Entry becomes Node because it is associated with TreeNode, the implementation of red black tree. The biggest difference between 1.8 and 1.7 is the use of red black tree, which is composed of array + linked list (or red black tree).

When analyzing hash conflicts in HashMap in jdk1.7, I wonder if you have a question: what if there are too many collision nodes? If hundreds of nodes collide in hash and are stored in a linked list, it will inevitably cost O(n) to find one of them This problem is finally solved in JDK1.8. In the worst case, the time complexity of linked list lookup is O(n), while the red black tree is always O(logn), which will improve the efficiency of HashMap.

HashMap in jdk1.7 adopts the method of bit bucket + linked list, which is often called hashing linked list, while jdk1.8 adopts the method of bit bucket + linked list / red black tree, which is also non thread safe. When the length of the linked list of a bit bucket reaches a certain threshold, the linked list will be converted into red black tree.

In jdk1.8, when the number of nodes with the same hash value is not less than 8, it will no longer be stored in the form of a single linked list and will be adjusted into a red black tree (null nodes in the above figure are not drawn). This is the biggest difference between the implementation of HashMap in jdk1.7 and jdk1.8.

HashMap solves conflicts according to the chain address method (zipper method). In jdk1.8, if the length of the linked list is greater than 8 and the length of the node array is greater than 64, all nodes under the linked list will be turned into a red black tree.

By analyzing the source code of the put method, this difference can be made more intuitive:

static final int TREEIFY_THRESHOLD = 8;
 
public V put(K key, V value) {
        return putVal(hash(key), key, value, false, true);
 }
  
  
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
                   boolean evict) {
        Node<K,V>[] tab;
    Node<K,V> p;
    int n, i;
    //If there is no data in the current map, execute the resize method and return n
        if ((tab = table) == null || (n = tab.length) == 0)
            n = (tab = resize()).length;
     //If the key value pair to be inserted has no element at the location where it is stored, it can be encapsulated as a Node object and placed at this location
        if ((p = tab[i = (n - 1) & hash]) == null)
            tab[i] = newNode(hash, key, value, null);
    //Otherwise, there are elements on it
        else {
            Node<K,V> e; K k;
        //If the key of this element is the same as that to be inserted, replace it.
            if (p.hash == hash &&
                ((k = p.key) == key || (key != null && key.equals(k))))
                e = p;
        //1. If the current node is data of TreeNode type, execute putTreeVal method
            else if (p instanceof TreeNode)
                e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
            else {
        //Or traverse the data on this chain, which is no different from jdk7
                for (int binCount = 0; ; ++binCount) {
                    if ((e = p.next) == null) {
                        p.next = newNode(hash, key, value, null);
            //2. After completing the operation, do one more thing, judge, and possibly execute the treeifyBin method
                        if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                            treeifyBin(tab, hash);
                        break;
                    }
                    if (e.hash == hash &&
                        ((k = e.key) == key || (key != null && key.equals(k))))
                        break;
                    p = e;
                }
            }
            if (e != null) { // existing mapping for key
                V oldValue = e.value;
                if (!onlyIfAbsent || oldValue == null) //true || --
                    e.value = value;
           //3.
                afterNodeAccess(e);
                return oldValue;
            }
        }
        ++modCount;
    //Judge the threshold and decide whether to expand the capacity
        if (++size > threshold)
            resize();
        //4.
        afterNodeInsertion(evict);
        return null;
    }

The special features of the above codes are as follows:

if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
       treeifyBin(tab, hash);

treeifyBin() is to convert the linked list into a red black tree.

The process of tree operation is a little complex, which can be seen in combination with the source code. Convert the original single linked list into a two-way linked list, and then traverse the two-way linked list into a red black tree.

final void treeifyBin(Node<K,V>[] tab, int hash) {
     int n, index; Node<K,V> e;
     //Another requirement for tree formation is that the array length must be greater than or equal to 64, otherwise continue to adopt the capacity expansion strategy
     if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
         resize();
     else if ((e = tab[index = (n - 1) & hash]) != null) {
         TreeNode<K,V> hd = null, tl = null;//hd points to the first node and tl points to the tail node
         do {
             TreeNode<K,V> p = replacementTreeNode(e, null);//Convert linked list nodes into red black tree nodes
            if (tl == null) // If the tail node is empty, there is no first node
                hd = p;  // The current node is the first node
            else { // If the tail node is not empty, construct a two-way linked list structure and append the current node to the end of the two-way linked list
                p.prev = tl; // The previous node of the current tree node points to the tail node
                tl.next = p; // The last node of the tail node points to the current node
            }
            tl = p; // Set the current node as the tail node
        } while ((e = e.next) != null); // Continue to traverse the single linked list
        //Convert the original single linked list into a two-way linked list with a node type of TreeNode
        if ((tab[index] = hd) != null) // Replace the converted two-way linked list with the one-way linked list in the original position of the array
            hd.treeify(tab); // Tree the current two-way linked list
    }
}

You should pay special attention to one thing. A requirement of treelization is that the array length must be greater than or equal to MIN_TREEIFY_CAPACITY (64), otherwise continue to adopt the capacity expansion strategy.

Generally speaking, HashMap stores elements in the form of array + single linked list by default. When there is a hash conflict between elements, it will be stored in the single linked list at that location. However, the single linked list will not always add elements. When the number of elements exceeds 8, it will try to convert the single linked list into red black tree storage. However, before conversion, the length of the current array will be judged again. Only when the array length is greater than 64 can it be processed. Otherwise, expand the capacity.

The realization of converting bidirectional linked list into red black tree:

 final void treeify(Node<K,V>[] tab) {
     TreeNode<K,V> root = null;  // Defines the root node of the red black tree
     for (TreeNode<K,V> x = this, next; x != null; x = next) { // Start traversing one by one from the head node of the TreeNode bidirectional linked list
         next = (TreeNode<K,V>)x.next; // Successor node of head node
         x.left = x.right = null;
         if (root == null) {
             x.parent = null;
             x.red = false;
             root = x; // The head node is set to black as the root of the red black tree
        }
        else { // There is a root node in the red black tree
            K k = x.key; 
            int h = x.hash;
            Class<?> kc = null;
            for (TreeNode<K,V> p = root;;) { // Traverse the entire red black tree from the root
                int dir, ph;
                K pk = p.key;
                if ((ph = p.hash) > h) // The hash value of the current red black tree node p is greater than the hash value of the bidirectional linked list node x
                    dir = -1;
                else if (ph < h) // The hash value of the current red black tree node is less than the hash value of the two-way linked list node x
                    dir = 1;
                else if ((kc == null &&
                          (kc = comparableClassFor(k)) == null) ||
                         (dir = compareComparables(kc, k, pk)) == 0) // The hash value of the current red black tree node is equal to the hash value of the two-way linked list node x. if the key value is consistent with the comparator, the key value will be compared
                    dir = tieBreakOrder(k, pk); //If the key values are the same, the className and identityHashCode are compared

                TreeNode<K,V> xp = p; 
                if ((p = (dir <= 0) ? p.left : p.right) == null) { // If the current red black tree node p is a leaf node, the bidirectional linked list node x finds the insertion position
                    x.parent = xp;
                    if (dir <= 0) //Insert the left child or right child of p according to the value of dir
                        xp.left = x;
                    else
                        xp.right = x;
                    root = balanceInsertion(root, x); //Elements as like as two peas in red and black trees need balance adjustment (the process is exactly the same as TreeMap adjustment logic).
                    break;
                }
            }
        }
    }
    //After the TreeNode bidirectional linked list is transformed into a red black tree structure, since the red black tree is searched based on the root node, the root node of the red black tree must be used as the element of the current position of the array
    moveRootToFront(tab, root);
}

Then move the root node of the red black tree to the index position of the mobile end array:

static <K,V> void moveRootToFront(Node<K,V>[] tab, TreeNode<K,V> root) {
     int n;
     if (root != null && tab != null && (n = tab.length) > 0) {
         int index = (n - 1) & root.hash; //Find the position of the red black tree root node in the array
         TreeNode<K,V> first = (TreeNode<K,V>)tab[index]; //Gets the element at that position in the current array
         if (root != first) { //The red black tree root node is not an element of the current position of the array
             Node<K,V> rn;
             tab[index] = root;
             TreeNode<K,V> rp = root.prev;
            if ((rn = root.next) != null) //Connect the front and back nodes of the red black tree root node
                ((TreeNode<K,V>)rn).prev = rp;
            if (rp != null)
                rp.next = rn;
            if (first != null) //Take the element of the current position of the array as the successor node of the root node of the red black tree
                first.prev = root;
            root.next = first;
            root.prev = null;
        }
        assert checkInvariants(root);
    }
}

The putVal method handles a lot of logic, including initialization, capacity expansion and tree, which can be reflected in this method. For the source code, briefly explain the following key points:

If node < K, V > [] table is null, the resize method will be responsible for initialization, that is, the following code:

if ((tab = table) == null || (n = tab.length) == 0)
    n = (tab = resize()).length;

The resize method takes into account two responsibilities, creating an initial storage table or resizing when the capacity does not meet the demand.
During the process of placing new key value pairs, capacity expansion will occur if the following conditions occur.

if (++size > threshold)
    resize();

The position of the specific key value pair in the hash table (array index) depends on the following bit operations:

i = (n - 1) & hash

If you carefully observe the source of the hash value, you will find that it is not the hashCode of the key itself, but another hash method inside the HashMap. Why is it necessary to shift the high-order data to the low-order for XOR operation? This is because the hash value difference calculated from some data is mainly in the high order, and the hash addressing in HashMap ignores the high order above the capacity, so this processing can effectively avoid hash collision in similar cases.

In jdk1.8, the indefFor() method is canceled and (tab. Length-1) & hash is directly used. Therefore, when you see this, it represents the subscript of the array.

static final int hash(Object key) {
    int h;
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

Why should HashMap be treelized?

I saw an explanation in the geek time column before. This is essentially a security issue. Because in the process of element placement, if an object hash conflict is placed in the same bucket, a linked list will be formed. We know that the linked list query is linear, which will seriously affect the access performance. In the real world, the construction of hash conflict data is not very complex. Malicious code can use these data to interact with the server, resulting in a large amount of CPU occupation on the server, which constitutes a hash collision denial of service attack. Similar attacks have occurred in domestic front-line Internet companies.

Denial of service attack (DOS, denial of service) with hash collision
attack), a common scenario is that an attacker can construct a large number of data with the same hash value in advance, and then send it to the server in the form of JSON data. In the process of building it into a Java object, the server usually stores it in the form of Hashtable or HashMap. Hash collision will lead to serious degradation of the hash table, and the complexity of the algorithm may increase by one data level, Thus, it consumes a lot of CPU resources.

Why set the threshold of red black tree in linked list to 8?

We can see that when the length of the linked list is greater than or equal to the threshold (the default is 8), if the capacity is greater than or equal to min_ TREEIFY_ According to the requirements of capability (64 by default), the linked list will be converted into a red black tree. Similarly, if the size is adjusted due to deletion or other reasons, when the number of nodes in the red black tree is less than or equal to 6, it will return to the linked list form.

Each time we traverse a linked list, the average search time complexity is O(n), and N is the length of the linked list. The red black tree has different search performance from the linked list. Because the red black tree has the characteristics of self balancing, it can prevent the occurrence of imbalance, so the time complexity of search can always be controlled at O(log(n)). At first, the linked list is not very long, so there may be little difference between O(n) and O(log(n)), but if the linked list becomes longer and longer, this difference will be reflected. Therefore, in order to improve the search performance, we need to convert the linked list into the form of red black tree.

It is also important to note that the space occupied by a single TreeNode is about twice that of an ordinary Node, so it will be converted to TreeNodes only when there are enough Nodes, and whether there are enough Nodes is determined by treeify_ Determined by the value of threshold. When the number of Nodes in the bucket is reduced due to removal or resize, it will change back to the form of ordinary linked list to save space.

The default is that when the length of the linked list reaches 8, it will be converted into a red black tree, and when the length is reduced to 6, it will be converted back, which reflects the idea of time and space balance. When the linked list is first used, the space occupation is relatively small, and because the linked list is short, there is no big problem in query time. However, when the linked list becomes longer and longer, we need to use the form of red and black tree to ensure the efficiency of query.

In the ideal case, the length of the linked list conforms to the Poisson distribution, and the hit probability of each length decreases in turn. When the length is 8, it is the most ideal value.

In fact, the design of turning the linked list into a red black tree when the length of the linked list exceeds 8 is more to prevent the linked list from being too long when the user implements a bad hash algorithm, resulting in low query efficiency. At this time, turning into a red black tree is more of a minimum guarantee strategy to ensure the efficiency of query in extreme cases.

Generally, if the hash algorithm is normal, the length of the linked list will not be very long, and the red black tree will not bring obvious advantages in query time, but will increase the burden of space. Therefore, generally, it is not necessary to convert to red black tree, so the probability is very small, less than one in ten million, that is, the probability of length 8, and length 8 is taken as the default threshold for conversion.

If a red black tree structure is found in the HashMap during development, there may be a problem with our hash algorithm, so we need to select an appropriate hashCode method to reduce conflicts.

4, Analyze the differences among Hashtable, HashMap and TreeMap

• HashMap inherits from AbstractMap class, while HashTable inherits from Dictionary class. However, they all implement map, Cloneable and Serializable interfaces at the same time. The stored content is a key value pair mapping based on key value. There can be no duplicate keys, and a key can only map one value- The bottom layer of HashSet is implemented based on HashMap.
• The key and value of Hashtable cannot be null; The key and value of HashMap can be null, but only one key can be null, but there can be multiple null values; TreeMap key and value cannot be null.
• Hashtable and HashMap are disordered. TreeMap is implemented by using red black tree (the value of each node in the tree will be greater than or equal to the value of all nodes in its left subtree and less than or equal to the value of all nodes in its right subtree). It implements the SortMap interface and can sort the saved records according to the key. Therefore, TreeMap is preferred for general sorting. By default, the keys are sorted in ascending order (depth first search). You can also customize the Comparator interface to realize the sorting method.
  In general, we choose HashMap because the key value pairs of HashMap are random when taken out. It accesses data according to the hashCode of the key and the equals method of the key, which has a fast access speed. Therefore, it is the most efficient implementation when inserting, deleting and indexing elements in the Map. The key value pairs of TreeMap are sorted when they are taken out, so the efficiency will be low.

TreeMap is a Map that provides sequential access based on red black tree. Different from HashMap, its get, put and remove operations are o(log(n)) time complexity. The specific order can be determined by the specified Comparator or according to the natural order of keys.

The following is a summary of HashMap:
HashMap is based on Hash hash table, which can read and write data. When the key value pair is passed to the put method, it calls the hashCode() method of the key object to calculate the hashCode, and then finds the corresponding bucket location (i.e. array) to store the value object. When getting the object, find the correct key value pair through the equals() method of the key object, and then return the value object. HashMap uses the linked list to solve the hash conflict. When a conflict occurs, the object will be stored in the head node of the linked list. HashMap stores key value pair objects in each linked list node. When the hashcodes of two different key objects are the same, they will be stored in the linked list at the same bucket location. If the linked list size exceeds the threshold (tree_threshold, 8), the linked list will be transformed into a tree structure.

There is a question to make a special statement:

• HashMap uses the header insertion method in jdk1.7. During capacity expansion, the original order of elements in the linked list will be changed, so that the linked list will become a ring in a concurrent scenario.
• The tail insertion method is adopted in jdk1.8. The original order of linked list elements will be maintained during capacity expansion, so the problem of linked list forming a ring will not occur.

We can simply list the changes of HashMap between 1.7 and 1.8:

• Array + linked list is used in 1.7, and array + linked list / red black tree is used in 1.8, that is, after the length of the linked list in 1.7 exceeds a certain length, it will be stored in red black tree.
• 1.7 the hash value and index position need to be recalculated during capacity expansion. 1.8 does not recalculate the hash value, but skillfully uses and capacity after capacity expansion to calculate the new index position.
• 1.7 uses the header insertion method to insert the linked list, and 1.8 uses the tail insertion method.
• In 1.7, the header insertion method is adopted, which will change the original order of elements in the linked list during capacity expansion, so that the linked list becomes a ring in the concurrent scenario; In 1.8, the tail insertion method is adopted. During capacity expansion, the original order of linked list elements will be maintained, and the problem of linked list forming a ring will not occur.

5, Differences among HashMap, Hashtable and ConcurrentHashMap

HashTable

• The underlying array + linked list implementation, whether key or value can not be null, is thread safe. The way to achieve thread safety is to lock the entire HashTable when modifying data, which is inefficient. ConcurrentHashMap has been optimized
• Initial size is 11, capacity expansion: newsize = olesize*2+1
• How to calculate index: index = (hash & 0x7fffffff)% tab.length

HashMap

• The underlying array + linked list implementation can store null keys and null values, and the thread is unsafe
• The initial size is 16, the capacity expansion is: newsize = oldsize*2, and the size must be the n-th power of 2
• For the entire Map, the storage location of the elements in the original array will be recalculated and reinserted each time
• Judge whether to expand the capacity after inserting the element, which may be invalid (if the element is expanded after insertion, if it is not inserted again, it will produce invalid expansion)
• When the total number of elements in the Map exceeds 75% of the Entry array, the capacity expansion operation is triggered. In order to reduce the length of the linked list, the elements are distributed more evenly
• Calculation method of index: index = hash & (tab. Length – 1)

ConcurrentHashMap

• The bottom layer is realized by segmented array + linked list, which is thread safe
• By dividing the whole Map into n segments, the same thread safety can be provided, but the efficiency is increased by N times, and the default is increased by 16 times. (the read operation is unlocked. Since the value variable of HashEntry is volatile, it is also guaranteed to read the latest value.)
• The synchronized Hashtable is for the entire Hash table, that is, locking the entire table every time allows the thread to monopolize it. Concurrent HashMap allows multiple modification operations to be performed concurrently. The key is the use of lock separation technology
• Some methods need to span segments, such as size() and containsValue(). They may need to lock the entire table rather than just a segment. This requires locking all segments in order. After the operation is completed, they release the locks of all segments in order
• Capacity expansion: capacity expansion within the segment (if the element in the segment exceeds 75% of the length of the corresponding Entry array of the segment, the capacity expansion will be triggered, and the entire Map will not be expanded). Whether the capacity expansion is required is detected before insertion to effectively avoid invalid capacity expansion

When calculating the container index, first calculate the hash value through the key value, that is, hash = key.hashCode() in the formula.